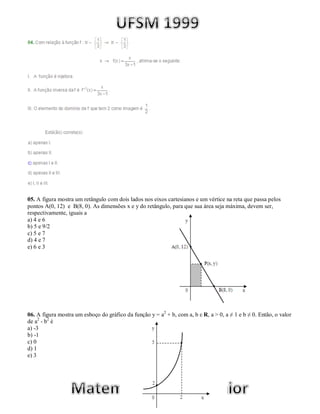
I. O produto dos elementos que formam o conjunto (A ∩ B) - C é igual a 15. II. O ponto de interseção da reta AB com o eixo x tem abscissa igual a a - 2. III. As dimensões x e y do retângulo, para que sua área seja máxima, devem ser, respectivamente, iguais a 5 e 7.

1. 01. Dados os conjuntos A = { x ε N/ x é ímpar}, B = { x ε Z/ -2 < x ≤ 9 } e C = { x ε R/ x ≥ 5}, o produto dos
elementos que formam o conjunto ( A ∩ B ) - C é igual a
a) 1
b) 3
c) 15
d) 35
e) 105
03. A figura representa o gráfico de uma função do 1º grau que passa pelos pontos A e B, onde a ≠ 2.
O ponto de interseção da reta AB com o eixo x tem abscissa igual a
a) 1 - a
b) a - 2
c)
d) 4 - a
e) 12 - 3a

2. 05. A figura mostra um retângulo com dois lados nos eixos cartesianos e um vértice na reta que passa pelos
pontos A(0, 12) e B(8, 0). As dimensões x e y do retângulo, para que sua área seja máxima, devem ser,
respectivamente, iguais a
a) 4 e 6
b) 5 e 9/2
c) 5 e 7
d) 4 e 7
e) 6 e 3
06. A figura mostra um esboço do gráfico da função y = a2 + b, com a, b ε R, a > 0, a ≠ 1 e b ≠ 0. Então, o valor
de a2 - b2 é
a) -3
b) -1
c) 0
d) 1
e) 3

3. 07. Considere as afirmativas:
I. Se log3(x + y) = a e x - y = 9, então log3(x2 - y2) = a +2.
II. Seja g(x) = ax a função exponencial de base a com 0 < a < 1. Para x1 < x2, tem-se g(x1) < g(x2).
III. Se f(x) = 3x, x ε R, então f(a + 1) - f(a) = 2f(a).
Está(ão) correta(s)
a) apenas I.
b) apenas II.
c) apenas I e III.
d) apenas II e III.
e) I, II e III.
09. Numa progressão aritmética crescente, os dois primeiros termos são as raízes da equação x2 + 2x - 8 = 0.
Sabendo que o número de termos dessa P.A. é igual ao triplo da sua razão, então a soma dos termos da P.A. é
igual a
a) -378
b) -282
c) 98
d) 294
e) 846
10. Um estudante de Engenharia vê um prédio do Campus da UFSM construído em um terreno plano, sob um
ângulo de 30º. Aproximando-se do prédio mais 40 m, passa a vê-lo sob um ângulo de 60º. Considerando que a
base do prédio está no mesmo nível do olho do estudante, então a altura h do prédio é igual a
a) 30√3 m
b) 20√3m
c) 30 m
d) 10√3m
e) 28 m

4. 12. A função f(x) = sen x, x ε R, tem como gráfico a senóide que, no intervalo [0, 2π], está representada na
figura
Se g(x) = a sen 3x, onde a ε R e a ≠ 0, assinale verdadeira (V) ou falsa (F) em cada uma das afirmações a
seguir.
( ) O domínio da função g é igual ao domínio da função f, independente do valor de a.
( ) Para todo a, o conjunto imagem da função f está contido no conjunto imagem da função g.
( ) O período da função g é maior que o período da função f.
A sequência correta é
a) V - F - F . b) V - V - F . c) F - V - V . d) V - F - V . e) F - V - F .
13. Sejam A e B matrizes reais quadradas de ordem n e O a matriz nula de ordem n. Então, a afirmativa correta
é a seguinte:
a) Se At é a matriz transposta de A, então det At ≠ det A.
b) Se det A ≠ 0, existe a matriz inversa A-1 e , onde cof A é a matriz dos cofatores de A.
c) Se A.B = 0, então A = 0 ou B = 0.
d) (A - B )2 = A2 - 2AB + B2.
e) Se k ε R, então det (kA) = kdet A, para todo k.

5. 14. Dadas as matrizes
onde m é o termo independente do desenvolvimento do binômio
então o determinante da matriz Q = M . N é igual a
a) 15
b) 126
c) 374
d) -126
e) -156
15. Considere o seguinte sistema de equações lineares:
Então, pode-se afirmar que o sistema é
a) impossível.
b) possível e determinado.
c) possível e qualquer solução (x, y, z, t) é tal que os números x, y, z, t formam, nessa ordem, uma progressão
aritmética.
d) possível e qualquer solução (x, y, z, t) é tal que os números x, y, z, t formam, nessa ordem, uma progressão
geométrica.
e) possível, porém não admite a solução nula.
16. Numa Câmara de Vereadores, trabalham 6 vereadores do partido A, 5 vereadores do partido B e 4
vereadores do partido C. O número de comissões de 7 vereadores que podem ser formadas, devendo cada
comissão ser constituída de 3 vereadores do partido A, 2 vereadores do partido B e 2 vereadores do partido C, é
igual a
a) 7
b) 36
c) 152
d) 1200
e) 28800
17. Um poliedro convexo tem 12 faces triangulares e as demais, pentagonais. Sabendo que o número de arestas
é o triplo do número de faces pentagonais, então a soma dos ângulos de todas as faces pentagonais é, em
radianos, igual a
a) 3π
b) 12π
c) 36π
d) 64π
e) 108π

6. 18. Um técnico agrícola utiliza um pluviômetro na forma de pirâmide quadrangular regular, para verificar o
índice pluviômetro de uma certa região. A água, depois de recolhida, é colocada num cubo de 10 cm de aresta.
Se, na pirâmide, a água atinge uma altura de 8 cm e forma uma pequena pirâmide de 10 cm de apótema lateral,
então a altura atingida pela água no cubo é de
a) 2,24 cm
b) 2,84 cm
c) 3,84 cm
d) 4,24 cm
e) 6,72 cm
19. Sejam r: x + qy - 1 = 0 e s: px + 5y + 2 = 0 duas retas perpendiculares entre si. Então, é correto afirmar
que
a) p/q = -5
b) p/q = 5
c) p/q = 1
d) p.q = -1
e) p.q = 5
20. Dada a circunferência β: x2 + y2 - 4x - 12 = 0, então a circunferência α, que é concêntrica à circunferência β
e tangente à reta r: x + y = 0, é
a) x2 + ( y + 2)2 = 4
b) y2 - 4x + y2 = 0
c) x2 + y2 + 4y + 2 = 0
d) x2 + y2 - 4x + 2 = 0
e) (x + 2)2 + y2 = 2
21. Seja z = a + bi um número complexo, onde a, b ε R, a ≠ 0 e b ≠ 0. A área do polígono, cujos vértices são
z1 = z, z2= , z3 = -z e z4 = bi, é igual a
a) ab
b) (3/2).ab
c) 2ab
d) 3ab
e) 6ab
22. Assinale verdadeira (V) ou falsa (F) em cada uma das afirmações a seguir, referentes ao polinômio p(x) =
anxn + an-1xn-1 + ... + a2x2 + a1x + a0, onde n ≥1 e a0, a1, a2, ..., an são números reais.
( ) O polinômio p(x) é divisível por (x - a), se e somente se p(a) ≠ 0.
( ) O resto da divisão de p(x) por (x - a) é p(a).
( ) Se z = a + bi, com a, b ε R e b ≠ 0, é raiz da equação p(x) = 0, então o conjugado de z, é também raiz da
equação.
A sequência correta é
a) F - V - V.
b) F - F - V.
c) V - V - V.
d) F - V - F.
e) V - F - F.

7. 23. Sabendo que uma das raízes da equação 2x3 - 3x2 - x + m = 0 é solução de
com 0 ≤ θ ≤ π, então o produto das raízes da equação polinomial é
a) -1/2
b) 3/2
c) 12
d) 16
e) 24