1) O documento apresenta uma série de exercícios sobre matrizes, determinantes e sistemas lineares. 2) Os exercícios envolvem cálculo de determinantes, produto e inversa de matrizes, resolução de sistemas lineares e equações. 3) As questões apresentam diferentes níveis de complexidade e abordam conceitos fundamentais de álgebra linear.

1. 1
EXERCÍCIOS 2º ANO ENS. MÉDIO 2012
PROFº. JAIRO WEBER
MATRIZES E DETERMINANTES
1. A partir da matriz 22)( xijaA 
cujo
jiaij 23 
e 22)( xijbB 
, dado por
jibij 
, determine o valor de BA .
2. Utilizando as matrizes do exercício anterior,
determine a matriz (X), tal que, XBAt
 .
(A) 







64
53
(B) 





64
03
(C) 





04
53
(D) 





64
53
(E)
N.d.a.
3. Sendo a matriz 33)( xijbB  cujo jibij  ²
determine o valor numérico da soma dos
elementos da diagonal principal da matriz B.
a)12 b) 16 c)20 d)24
e) 28
4. O termo da terceira linha e segunda coluna
da matriz 3)( ijaA  cujo jiaij
3
2
2
1
 é:
a)11/5 b) 16/6 c)20/3 d)17/6
e) n.d.a.
5. (UPF) Na matriz 45)( xijaA  , onde
²4 jiaij  , o valor de 522 a é:
(A)16
(B)24
(C)32
(D)48
(E)64
6. (U.F. Lavras) Seja  ijaA  uma matriz de
ordem 3x3, dada por






ji
jiji
aij
,1
,
. A
matriz pode ser escrita como.
(A)










654
543
422
(B)










154
513
431
(C)










143
412
221
(D)










143
512
431
(E)










054
503
430
7. Calcule BA , sendo 







42
31
A e





 

13
20
B .

2. 2
(A) 





 812
19
(B) 





 812
19
(C) 







812
19
(D) 





812
19
(E)
N.d.a.
8. Calcule


















15
42
31
524
132
.
(A) 







925
193
(B) 





 925
193
(C) 





 925
83
(D) 





 825
193
(E) N.d.a.
9. (PUC) Sendo











76
41
32
A e 






0
2
B ,
então o produto A.B é igual a:
(A)  1486
(B)











12
2
4
(C) 





00
64
(D)











1412
82
64
(E)











01412
801
640
10. (UFRGS) A matriz C fornece, em reais, o
custo das porções de arroz, carne e salada
usadas num restaurante:
salada
carne
arroz
C











2
3
1
A
matriz P fornece o número de porções de
arroz, carne e salada usados na composição
dos pratos tipo P1, P2, P3 desse restaurante:
3
2
1
022
121
112
pratoP
pratoP
pratoP
saladacarnearroz
C















A matriz que fornece o custo de produção, em
reais, dos pratos P1,P2, P3 é:
A.










8
9
7

3. 3
B.










4
4
4
C.










4
11
9
D.










8
6
2
E.










4
2
2
11. (UFRGS) Sendo mxmijaA )( uma matriz
quadrada de ordem 2 e jiaij  ² , o
determinante da matriz A é:
(A) -3.
(B) -1.
(C) 0.
(D) 1.
(E) 3.
12. (UFRGS) Se 







11
11
A , então ²A é a
matriz:
(A) 





 11
11
(B) 





00
00
(C) 





11
11
(D) 




 
11
11
(E) 





 22
22
13. (UFRGS) Se A é uma matriz 2x2 e detA =
5, então o valor de det 2A é:
(A) 5
(B) 10
(C) 20
(D) 25
(E) 40
14. A partir da matriz 22)( xijaA  cujo
jiaij 23  e 22)( xijbB  , dado por
jibij  , determine o valor de BA .
Resposta:






1411
107
15. Calcule a equação 53
21
4
 x
x
.
(A) 1.
(B) -1.
(C) -1/5.
(D) 0.
(E) 7/8.
16. (UFRGS) O valor de x, na equação
8
42
21
622
410
31




x
é:
(A) -3.
(B) 3.
(C) 2.

4. 4
(D) 1.
(E) 0.
17. (UCS) O valor de x na equação
38
2
43
122 xxx


é:
18. (UFRGS) Se
2
11

ba
, então
22
1313  ba
é:
(A) 3.
(B) 4.
(C) 6.
(D) 8.
(E) 12.
19. Calcule a determinante de












524
132
030
A .
20. (PUC) A solução da equação
0
314
013
212
2 



x é:
21. (Fuvest-SP)O valor de
301
541
322

é :
(A) 0
(B) 20
(C) 30
(D) 40
(E) 50
22. (UNIBAHIA-BA) Considerando a matriz











5
11
111
xx
xA e det(A)=4, pode-se afirmar
que o valor de x é igual a:
(A) 3.
(B) -3.
(C) -1.
(D) 1.
(E) 2.
23. (UFOR-CE) Se a matriz 22)( xijbB  é a
matriz inversa de 






13
20
A , então:
(A) .
6
1
11 b
(B) .112 b
(C) .121 b
(D) .122 b
(E)
3
1
22 b
24. Calcule a determinante de















1403
1021
0321
0020
A .
25. Calcule a determinante de














3000
0100
2122
3011
A .
SISTEMAS LINEARES.

5. 5
26. O valor de a para que





26
13
ayx
yx
tenha
solução é:
(A) 0a
(B) 1a
(C) 2a
(D) 1a
(E) N.d.a.
27. (PUC-RS) Para que o sistema





254
1
yx
kyx
seja impossível o valor de K deve
ser:
(A)1/5
(B)1/4
(C)1/3
(D)4/5
(E)5/4
28. (UFSM) O sistema





42
2
myx
yx
terá uma
única solução:
(A)somente para m  -2
(B)somente para m=4
(C)para qualquer número real.
(D)somente para m = 0
(E)para qualquer m  2.
29. (UFRGS) O sistema linear





24
1
myx
yx
é
possível e determinado se e somente se:
(A)m =2
(B)m = 4
(C)m  -4
(D)m  1
(E)4m=1
30. (PUC) O sistema








1
222
23
mzyx
mzyx
zymx
é
indeterminado, se m for igual a:
(A) 4.
(B) 3.
(C) 2.
(D) 1.
(E) 0.
31. (UFRGS) O conjunto das soluções (x, y,
z) do sistema





0
02
zyx
zyx
é:
(A)  
(B)  0;0;0
(C)  2;2;0
(D)   Rttt /;;0
(E)   Rttt /;0;
32. (UFRGS) A relação entre a e b que o
sistema





byx
ayx
186
93
seja compatível e
indeterminado é:
(A)a=b/2
(B)a=b/3.
(C)a=b
(D)a=2b
(E)a=3b

6. 6
33. (UFRGS) O sistema





12
3
yx
nmyx
admite
infinitas soluções se, e somente se o valor de
m – n é:
(A)9
(B)6
(C)3
(D)1
(E)0
34. (UFRGS) O sistema








02
0
02
zyx
bzyax
zyx
com a
e b reais, é determinado se, e somente se,
(A)b=-a+1
(B)b  -a+1.
(C)b=a-1
(D)b  a-1
(E)b  a+1
35. (UFRGS) A soma dos valores de x, y e z
que verificam o sistema








05
12
103
zyx
zyx
zyx
é:
(A)-2
(B)-1
(C)0
(D)1
(E)2
36. A soma da terna x+y+z do seguinte
sistema








323
02
12
zyx
zyx
zyx
é:
A. 0.
B. 2.
C. 3.
D. 4.
E. 7.
37. (UFGO) Os valores de x, y e z, nesta
ordem, tais que








723
32
52
zyx
zy
yx
são:
(A)7/3; -5/3 e 4/3
(B) 4/3 ;-5/3 e 7/3
(C) 7/3; 4/3 e -5/3
(D) 4/3; 7/3 e -5/3
(E) -5/3 ; 4/3 e 7/3
ANÁLISE COMBINATÓRIA.
ARRANJO SIMPLES
38. Quantos números de três algarismos
distintos podemos formar com os elementos do
conjunto  5,4,3,2,1E ?
(A)20 (B)60 (C)30 ( D) 89
(E)N.d.a.
39. Uma empresa possui 16 funcionários
administrativos, entre os quais serão
escolhidos três, que disputarão para os cargos
de diretor, vice-diretor e tesoureiro. De
quantas maneiras pode ser feita a escolha?
(A)3200 (B) 3360 (C)3400 ( D)
5300 (E)5390
40. Júlio deseja pintar a palavra LIVRE em um
cartaz de publicidade, usando uma cor em cada
letra. De quantos modos isso pode ser feito, se
ele dispõe de 8 cores de tinta?

7. 7
(A) 890 (B)1234 (C) 89021 ( D)
6720 (E)N.d.a.
41. Quantos números de quatro algarismos
distintos podemos formar a partir dos
algarismos 3,4,5,6,7,8 e 9?
(A) 678 (B)840 (C) 422 ( D)
9098 (E)1024
42. Quantos números pares de quatro
algarismos distintos podemos formar a partir
dos algarismos 3,4,5,6,7,8 e 9?
(A)4321 (B) 3262 (C) 360 (
D)623 (E)620
43. Quantos números impares de quatro
algarismos distintos podemos formar a partir
dos algarismos 3,4,5,6,7,8 e 9?
(A) 480 (B) 9078 (C) 2521 (
D) 5322 (E)6433
44. Quantos números de quatro algarismos
distintos podemos formar a partir dos
algarismos 3,4,5,6,7,8 e 9 que comecem com
4?
(A)24 (B) 120 (C) 720 ( D)64
(E)243
45. Quantos números de quatro algarismos
distintos podemos formar a partir dos
algarismos 3,4,5,6,7,8 e 9 que comecem com 3
e terminem com 9?
(A) 20 (B)10 (C) 2! ( D) 42
(E)120
46. Quantos números de quatro algarismos
distintos podemos formar a partir dos
algarismos 0,1,2,3,4 e 5?
(A) 432 (B) 222 (C) 300 (
D)523 (E)4300
47. Quantos números de quatro algarismos
distintos podemos formar a partir dos
algarismos 1,2,3,4,5, e 6?
(A) 12 (B)21 (C)100 ( D) 360
(E)480
48. Quantos números ímpares com três
algarismos podemos formar a partir de
0,1,2,3,4,5 e 6?
(A) 21 (B) 32 (C)40 ( D)44
(E) 75
PERMUTAÇÃO SIMPLES
49. Quantos anagramas podemos formar a
partir da palavra LIVRES?
(A) 90 (B) 720 (C) 360 ( D)321
(E)125
50. Quantos anagramas, que começam com a
letra S, podemos formar a partir da palavra
LIVRES?
(A) 120 (B)320 (C) 330 (
D)329 (E)328
51. Quantos anagramas, que começam com a
letra S e terminam com a letra I, podemos
formar a partir da palavra LIVRES?
(A) 24 (B)25 (C)26 ( D) 27
(E)28
52. Quantos anagramas, que começam com
uma vogal, podemos formar a partir da palavra
LIVRES?
(A) 120 (B) 240 (C)480 (
D)720 (E)422
53. Quantos anagramas, que começam e
terminam com vogais, podemos formar a partir
da palavra LIVRES?
(A) 12 (B) 48 (C) 36 ( D)56
(E)120
54. Quantos anagramas, que começam e
terminam com consoantes, podemos formar a
partir da palavra TRAPO?
(A) 36 (B) 42 (C) 44 ( D)54
(E)58
55. Quantos anagramas, que começam mantém
as letras I e V juntas, podemos formar a partir
da palavra LIVRES?
(A) 440 (B) 360 (C) 240 (
D)120 (E)60
56. Quantos anagramas, que mantém as letras
IV juntas e nessa ordem, podemos formar a
partir da palavra LIVRES?
(A) 120 (B)32 (C)142 ( D)523
(E)520
57. Sem repetir algarismos, quantas senhas
diferentes podemos formar com seis dígitos,
0,1,2,3,4 e 5?
(A)889 (B)990 (C) 908 (
D)909 (E) 720
58. O número de anagramas da palavra
FUVEST que começam e terminam com
vogais é:
(A) 32 (B)43 (C)66 ( D)45
(E) 48
COMBINAÇAO SIMPLES

8. 8
59. Nove professores de matemática se
candidataram a quatro vagas de um congresso,
calcular quantos grupos serão possíveis.
(A) 54 (B)56 (C)66 ( D)45
(E)126
60. Quantos grupos diferentes de quatro
lâmpadas podem ficar acesos num galpão que
tem 10 lâmpadas?
(A)120 (B)345 (C)126 ( D)645
(E)210
61. Quantos subconjuntos de 4 elementos
possuem um conjunto de seis elementos?
(A)1 (B)12 (C)24 ( D)54
(E)15
62. O número de combinações de n objetos
distintos tomados 2 a 2 é 15. Determine n.
(A) 2 (B)4 (C)5 ( D)6
(E) 16
63. Quantas comissões de 5 membros
podemos formar numa assembléia de 12
participantes?
(A)324 (B)235 (C)643 ( D)865
(E)792
64. Quantos produtos de 2 fatores podemos
obter com os divisores naturais do número 12?
(A)1 (B)2 (C)4 ( D)8
(E)15
PERMUTAÇÃO COM REPETIÇÃO
65. Qual é o número de anagramas que
podemos formar com as letras da palavra
URUGUAI?
(A)840 (B)124 (C)543 ( D)235
(E)849
66. Qual é o número de anagramas que
podemos formar com as letras da palavra
URUGUAIANA?
(A)108870 (B)34990 (C)43000 (
D) 100.800 (E)54000
67. Qual é o número de anagramas que
podemos formar com as letras da palavra
PÁSSARO?
(A) 1230 (B)2309 (C)4890 (
D)100800 (E)1.260
68. Qual é o número de anagramas que
podemos formar com as letras da palavra
ARARA?
(A) 3 (B) 4 (C) 12 ( D) 42
(E)10
69. A partir da palavra AMADA, o número de
anagramas formado é:
(A) 20 (B)30 (C) 40 ( D) 50
(E)60
NÚMEROS BINOMIAIS
70. Dado o número binomial 





18
20
, temos:
a)190 b)180 c)380 d)220 e)n.d.a.
71. Dado o binômio
5
2
1
2 





x , determine o
polinômio que representa sua solução:
72. O termo dependente 5
x do polinômio
desenvolvido a partir de  7
2x é:
a) 64 b)84 c)104 d)114 e)124
73. O termo independente de  6
1x é:
a) 32 b) -32 c)1 d)-1 e)n.d.a.

9. 9
74. O quarto termo T(5) do polinômio que
resulta de  52
2x é:
a) 2
80x b) 2
80x c) 4
80x d) 4
80x
e)n.d.a.
75. O termo que representa x³ dado a partir do
binômio
6
2
1
2 





x
76. Calculando o coeficiente numérico do
termo 8
x do polinômio dado a partir da
resolução do binômio  92
2x , temos:
a) 2430 b)4032 c)4320 d)2340 e)n.d.a
77. Determine o coeficiente numérico de x²
dado na expressão que resulta de  4
2x :
A. 24
B. -24
C. 4
D. 14
E. n.d.a.
POLINÔMIOS
78. (UFGRS) O polinômio (m² - 4)x³+(m-2)x²
- (m+3) é de grau 2 se, e somente se,
(A) m= - 2
(B) m= 2
(C) m = ±2
(D) m≠2
(E) m≠ -2
79. (UFRGS) O valor de a para que
    xaxxaaxa  ²³2²1 42
seja um
polinômio do 2º grau na variável x é:
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
80. (UFRGS) Se P(x) = 3x²+12x-7, então P(-1)
vale:
(A) -16
(B) -7
(C) 0
(D) 3
(E) 24
81. (UFRGS) O polinomio P(x) do 1º grau tal
que P(1)=5 e P(-1)=1 é:
(A) x+4
(B) 2x+3
(C) 3x+2
(D) 3x+4
(E) 5x
82. Dado o polinômio
  1234
 xxxxxP , então P(-1); P(1) e
P(-2), respectivamente são:
(A) -1; 3 ; 9
(B) -1; -3 ; 9
(C) -1; 3 ; -9
(D) 1; 3 ; 9
(E) -1; -3 ; -9
83. A partir do polinômio
  1234
 xxxxxP ,então 





2
1
P é:
(A)
16
1

(B)
16
5

(C)
16
1
(D)
5
1
(E) N.d.a.
84. Dado o polinômio
124)( 23
 xxxxp , calculando )3(p ,
obteremos:

10. 10
144
233
333
122
N.d.a.
85. Calcule a e b de modo que os polinômios
sejam idênticos P(x) = (2a +6)x³ + (3b-4)x² e
Q(x)=2x³+5x².
Resp. -2 e 3.
86. Dados os polinômios 65²2)(  xxxA e
106³)(  xxxB , dê o que se pede:
a) )()( xBxA  . Resp. 4²2³  xxx
b) )()( xBxA  . Resp. 1611²2³  xxx
c) )()( xAxB  . Resp. 1611²2³  xxx
d) )()( xBxA  . Resp.
6086²10³1852 45
 xxxxx
87. Sendo os polinômios
32)( 234
 xxxxxP e
32)( 23
 xxxxQ , calcule o valor
numérico de P(2) – Q( - 1).
(A) 8
(B) 12
(C) 28
(D) 90
(E) n.d.a.
88. Considere os polinômios xxxP  ³)( ,
42²³63)( 4
 xxxxxQ e calcule:
a)  ²)(xP . Resp. ²2 46
xxx 
b) ).().( xQxP Resp.
xxxxxxx 4²234463 34567

89. Obtenha o quociente e o resto de cada
divisão abaixo:
90. 43²)(  xxxA por 1)(  xxB
91. 1011²³)(  xxxxA por 2)(  xxB
92. 62²9³3)(  xxxxA por
2²3)(  xxB
93. 8²7)(  xxA por 3)(  xxB
94. xxxxA  ²5)( 4
por 1²)(  xxB
95. Dê o quociente e o resto da divisão de
944)( 234
 xxxxp por
1)( 2
 xxxg .
96. Determine o valor do resto da divisão entre
124)( 23
 xxxxp e 2)(  xxg ,
usando o teorema do resto.
97. (UFRGS) A divisão de P(x) por x²+1 tem
quociente x-2 e resto 1. O polinômio P(x) é:
(A) x²+x-1
(B) x²-x-1
(C) x²+x
(D) x³-2x²+x-2
(E) x³-2x²+x-1
98. (UFRGS) Na divisão do polinômio
A(x)=x³+x²-10x+8 pelo binômio x-1, obteve-
se o quociente Q(x). As raízes da equação
Q(x)=0 são:
(A) 0 e1
(B) -1 e 0
(C) -2 e 4
(D) -4 e 2

11. 11
(E) -1 e 2
99. Encontre o quociente da divisão do
polinômio 6²64
 xxx pelo binômio x +
2. Este exercício pode ser resolvido pelo
dispositivo de Briot-Ruffini.
100. (UFRGS) O quociente da divisão de
x³+5x-1 por x-2 é:
(A) x²+2x-19
(B) x²+x+3
(C) x²-2x+1
(D) x²+2x-1
(E) x²+2x+9
101. Calcule através do dispositivo de Briot-
Ruffini o quociente e o resto da divisão de
6583)( 23
 xxxxp por 2)(  xxg .
102. Determinar o valor de k, de modo que a
divisão do polinômio 4²3)(  xxxA pelo
binômio x+k seja exata.
103. Determinar, usando o dispositivo Briot-
Ruffini, o quociente e o resto da divisão do
polinômio 8²3³4)(  xxxA por
1)(  xxB
104. (UFGRS) Uma das raízes do polinômio
0189²2³  xxx é -2. A soma das outras
raízes é:
(A) -2
(B) -1
(C) 0
(D) 1
(E) 2
105. O polinômio representado no gráfico
abaixo é:
(A) 2²2³  xxx
(B) 2²5³  xxx
(C) 2²³  xxx
(D) xxx  ²³
(E) N.d.a.
106. (UFGRGS) Considere o gráfico abaixo.
Esse gráfico pode representar a função
definida por:
(A) 20²5³  xx
(B) 204²5³  xxx
(C) 420³54
 xxx
(D) 2045 34
 xxx
(E) xxxx 20²45 34

107. (Unicruz) Uma equação algébrica possui
como raízes os valores 4, 3 e 2. Esta equação
é:
(A) 044²3³2  xxx
(B) 082²³  xxx
(C) 02²2³  xxx
(D) 024269 23
 xxx
(E) 02²34 3
 xxx
108. (UFRGS) O resto da divisão de x³+ax²-
x+a por x-1 é 4. O valor de a é;
(A) 0
(B) 1
(C) -1
(D) 2

12. 12
(E) -2
109. (UFRGS) Para que o polinômio P(x) =
x²+(a-b)x-2a seja divisível por x-2, a e b
devem satisfazer:
(A) a qualquer número real e b = 2.
(B) a=2 e b qualquer numero real
(C) somente para a=2 e b=2.
(D) somente para a=0 e b=2
(E) a e b qualquer valor real.
TRIGONOMETRIA.
110. Um papagaio é empinado por um
garoto através de um barbante de 50m, com o
sol a pino a sombra do papagaio é projetada a
uma distância de 30 m do garoto exatamente
abaixo dele, calculando a altura do papagaio,
teremos:
a)40m b) 30m c) 10m d)24m e) N.d.a.
111. Uma escada de 40m está encostada no
topo do prédio formando, com o chão, um
ângulo de 60°. A altura do prédio é
aproximadamente:
a)45m b)25m c)55m d)35m e)N.d.a.
112. Para que a caçamba de um caminhão
basculante com 3,5m de comprimento
incline-se formando um ângulo de 45°, é
necessário que o hidráulico erga o outro lado,
em m:
a)1,75 b) 3,0 c) 1,0 d)2,4 e)N.d.a.
113. Um navio se aproxima da costa e avista
uma torre luminosa através de um ângulo de
30°, o capitão sabe que a torre está a 200 m
do nível do mar, fazendo alguns cálculos é
possível afirmar que o navio está distante da
costa, aproximadamente:
a)450m b)125m c)350m d)395m
e)320m
114. Um homem postado à 10m de uma
torre avista seu topo com um ângulo de 60°.
Qual é a altura aproximada dessa torre a
partir da cabeça do observador?
a)40,5m b)25,3m c)18,9m d)17,3m
e)N.d.a.
115. (PUC) De acordo com a figura, x, em
cm, é igual a
(A) 25
(B) 30
(C) 35
(D) 40
(E) 50
116. Um observador vê a torre vertical CD
sob um ângulo 30º e caminhando ate B passa
a vê-la sob um ângulo de 60º.
Sendo AB=40m, a altura da torre e a
distancia entre a torre e o observador,
posicionado em B, devem ser,
respectivamente.
(A) h=45m e d=30m
(B) h= mdem 15320 
(C) mdemh 20320 
(D) h=40m e d=20m
(E) h=50m e d=10m
117. Associe as colunas contendo ângulos
correspondentes:
a) 45° ( ) rad
4
3
b) 72° ( ) rad
5
2
c) 36° ( ) rad
4


13. 13
d) 135° ( ) rad
5

e) 600° ( ) rad
3
10
f) 60° ( ) rad
3
2
g) 120° ( ) rad
3

118. O arco de 480° equivale a:
(A) 120°
(B) 240°
(C) 90°
(D) 100°
(E) 190º
119. O arco de 495°:
(A) Está situado no 1º quadrante e é
côngruo à 85°
(B) Está situado no 2º quadrante e é
côngruo à 130°
(C) Está situado no 3º quadrante e é
côngruo à 215°
(D) Está situado no 2º quadrante e é
côngruo à 135°
(E) N.d.a.
120. O arco -157º é côngruo à:
a) 203°
b) 200°
c) 103°
d) 78°
121. O arco de
3
7
:
a) Está situado no 2º quadrante.
b) Está situado no 1º quadrante e é côngruo a
30°
c) Está situado no 2º quadrante e é côngruo à
135°
d) Está situado no 1º quadrante e é côngruo à
60°
122. O arco de
4
9
:
a) Está situado no 2º quadrante.
b) Está situado no 1º quadrante e é côngruo a
45°
c) Está situado no 2º quadrante e é côngruo à
135°
d) Está situado no 1º quadrante e é côngruo à
60°
123. Do arco
3
2
, temos seno e cosseno:
a)
2
3
2
1
e
b)
2
3
2
1
e
c)
2
1
2
3
e
d)
2
1
2
3
e
124. Usando as primeiras relações
trigonométricas podemos afirmar que
4
9
sen
:
a)
4
cos

b)
4

tg
c)
4

sen
d)
2
cos

125. 30sen é igual a:
a) Cosseno de 30°
b) Cosseno de 60°
c) Tangente de 30°
d) Tangente de 60°
126. (PUC) O valor de sen 1200° é:

14. 14
A. 1/2
B. -1/2
C.
2
3
D. -2/3
E. N.d.a.
127. O valor numérico de
 4560cosº30 tgsen é:
a) 1
b) 2
c) 3
d) 4
128. O valor numérico de
)²30()²30(cos sen é:
a)1 b)2 c)3 d)4
129. O valor numérico de
)²60()²60(cos  sen é:
a)1 b)2 c)3 d)4
130. Qual o valor numérico de
   ²45cos²45 sen ?
A. 1
B. 2
C. 3
D. 4
E. 5
131. Qual o menor ângulo entre os ponteiros
do relógio quando marca 12h45min?
132. Um garoto tem como tema de aula
descobrir o menor ângulo entre os ponteiros no
relógio municipal exatamente as 17h25min. O
que o menino deve responder?
a. Que é maior de 10°.
b. Que é exatamente 10°
c. Que é exatamente 5°.
d. Que é maior que 5° e menor que 10°
e. Que é menor que 5°.
133. Qual a medida do maior ângulo entre os
ponteiros do relógio ao marcar 9h40min?
134. Qual o ângulo que equivale a
4
7
rad?
135. O ângulo rad
12

equivale a:
136. Qual o valor numérico da expressão : sen
360° + sen540° - 4sen 1710°.
A. 4
B. 3
C. 2
D. 1
E. 0
137. Qual o valor numérico da expressão :
cos180°- 4. Cos3780°-1/2cos1350°.
A. -2
B. -1
C. 0
D. -3
E. -4
138. Qual o valor da expressão:
3
cos.cos
3
cos
4
cos8cos



 
? Resposta: 23
139. O valor da expressão cos 150° + sen
300° - tg225° - cos 90° é: Resposta: 13 
140. Qual o valor numérico de













4
8cos.
4
4
5cos
4
3cos2cos



sen
?
141. O valor de (sen 480°)² + (cos 405°)² –
(tg 210°)² é:
FUNÇÕES TRIGONOMÉTRICAS

15. 15
142. A função que melhor representa o
gráfico
é:
a. senxy  2
b.  2/.3 xseny 
c. senxy 21
d. xseny 2.2
e. xseny 2
143. A função que melhor representa o
gráfico
é:
a.  2/.3 xseny 
b. xseny 2
c. senxy 21
d. xseny 2.2
e. senxy  2
144. A função que melhor representa o
gráfico
é:
a. xseny 2
b. senxy  2
c. senxy 21
d. xseny 2.2
e.  2/.3 xseny 
145. A função que melhor representa o
gráfico é:
a.  2/.3 xseny 
b. senxy 21
c. senxy  2
d. xseny 2.2
e. xy cos2

16. 16
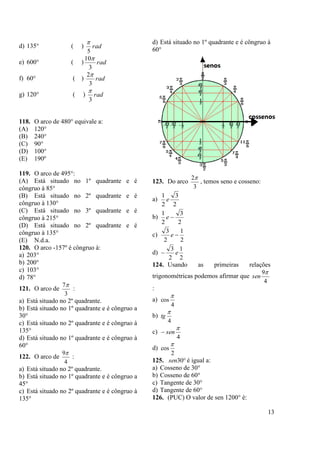
146. A função que melhor representa o
gráfico
é:
(A)  2/cos.3 xy 
(B) xy cos21
(C) xy cos2 
(D) xy 2cos.2
(E) xy cos2
213. A função que melhor representa o
gráfico
é:
a. xseny 2
b.  2/.3 xseny 
c. xseny 2.2
d. senxy  2
e. senxy 21
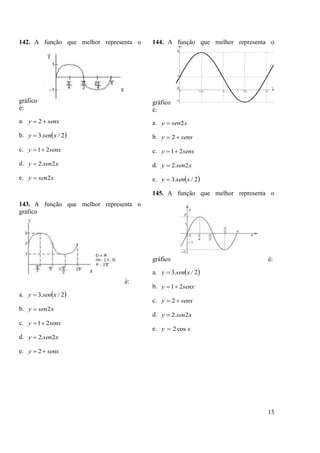
214. A função que melhor representa o
gráfico é:
(A)  2/cos.3 xy 
(B) xy cos21
(C) xy cos2 
(D) xy 2cos.2
(E) coxy 
215. A função xseny 2 tem como
característica:
a. Im=[-1;1] e p=2π
b. Im=[-1;3] e p=π
c. Im=[-1;2] e p=2π
d. Im=[-2;2] e p=π
e. Im=[-1;1] e p=π
216. A função senxy  2 tem como
característica:
a. Im=[1;3] e p=2π
b. Im=[-1;3] e p=π
c. Im=[-2;2] e p=2π
d. Im=[1;2] e p=π
e. Im=[1;3] e p=π
TRANSFORMAÇÕES
TRIGONOMÉTRICAS
absenbasenbasen cos.cos.)( 
absenbasenbasen cos.cos.)( 
bsenasenbaba .cos.cos)cos( 
bsenasenbaba .cos.cos)cos( 
btgatg
btgatg
batg
.1
)(



btgatg
btgatg
batg
.1
)(




17. 17
217. Exemplo – Determine o valor de
sen(75°): resp. sen(75°)=
4
26 
218. Calcule tg75°.
a. 32 
b.
4
32 
c.
4
26 
d.
2
26 
e.
6
36 
219. Calcule cos(15°).
a.
5
26 
b.
3
36 
c.
4
36 
d.
4
26 
e.
4
26 
220. Utilizando as fórmulas da adição,
determine sen 






3


a.
2
3

b.
2
3
c.
4
3

d.
2
2

e.
2
2
221. O valor de cos 






64

.
a.
2
3

b.
4
26 
c.
4
26 
d.
2
26 
e.
2
3
222. Qual o valor de sen(210°): Sugestão
(210°=180°+30°).
a. -1/2
b. 1/2
c. 3/5
d. -3/5
e. 1
223. )4( xsen  é o mesmo que:
a. Senx
b. –senx
c. Cosx
d. –cos x
e. tgx
224. )( xsen  é o mesmo que:
a. sen(x) b. –sen(x) c. cos(x) d. –cos(x)
e. n.d.a.
FÓRMULAS DA MULTIPLICAÇÃO.
aasenasen cos..2)2( 
asenaa ²²cos)2cos( 
atg
atg
atgatg
atgatg
aatgatg
²1
2
.1
)()2(





225. Sendo 2
0,
5
4
)(

 acomasen ,
calcule sen(2a):
a. 24/25.
b. 20/11
c. 23/54
d. 12/5
e. 211/35

18. 18
226. Sendo 2
0,
5
4
)(

 acomasen ,
calcule cos (2a):
a. 24/25.
b. -7/25
c. 23/54
d. -24/7
e. 17/25
227. Sendo 2
0,
5
4
)(

 acomasen ,
calcule tg(2a):
a. 24/25.
b. -7/25
c. 23/54
d. -24/7
e. 17/25
228. Sabendo que sen(a)=1/2, calcule sen(2a):
a.
2
3
b.
2
3

c.
2
3
d.
2
2
e.
2
1

229. Dado cos a =
2
3
, determine o valor de
cos(2a):
a.
2
3
b.
2
3

c.
2
3
d.
2
2
e.
2
1
230. Dado tg(x)=1/2, calcule tg(2x):
a. 1/2
b. 2/3
c. 3/4
d. 4/3
e. 1/3
231. Usando a afirmação anterior, tg(x)=1/2,
calcule cotg(2x):
a. 1/2
b. 2/3
c. 3/4
d. 4/3
e. 1/3
232. Sabe-se que cos(x) =4/5, com 0<x<90°.
Nessas condições calcule o valor numérico da
soma cos2x+sen2x:
(A) 23/25
(B) 31/24
(C) 31/25
(D) 12/15
(E) 13/25