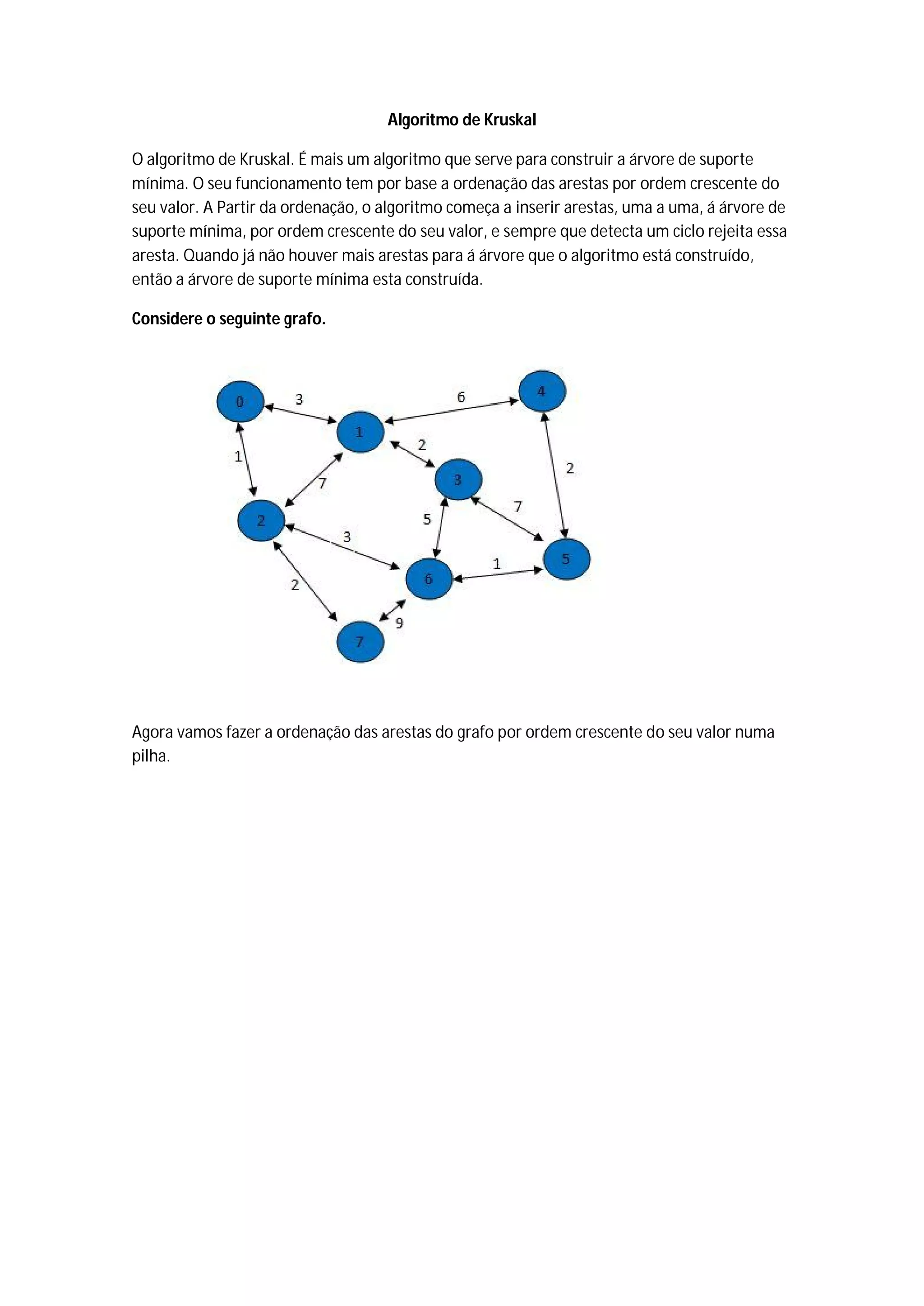
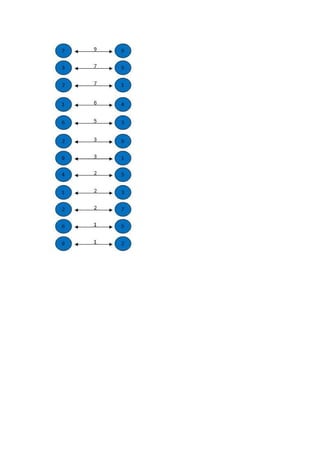
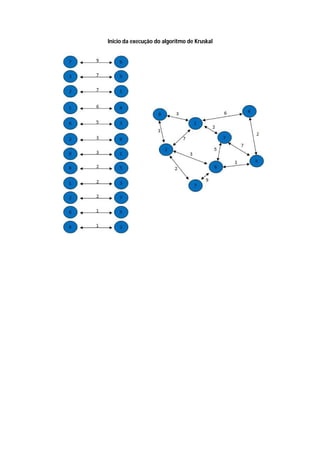
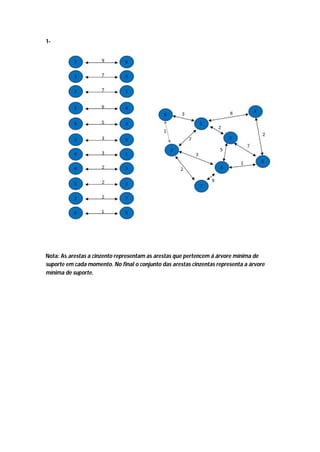
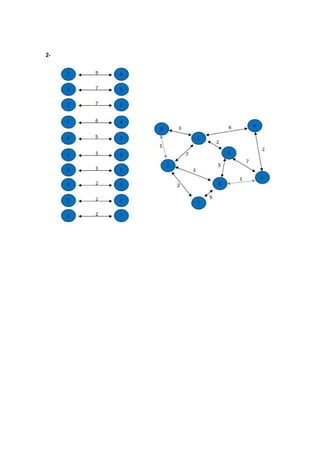
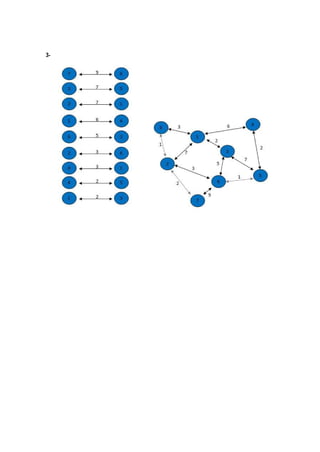
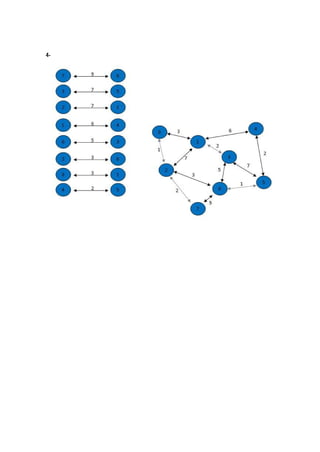
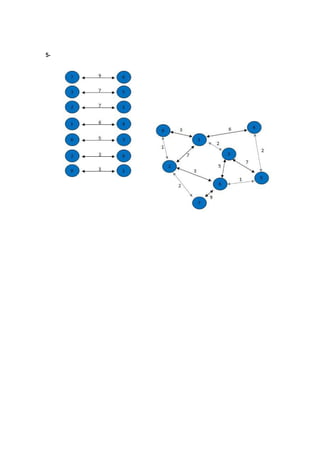
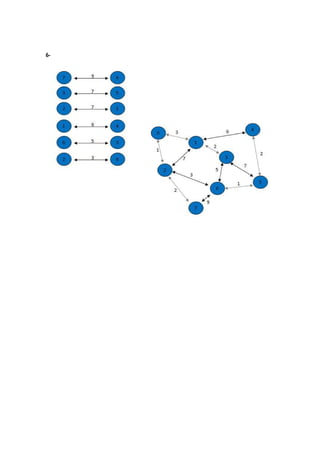
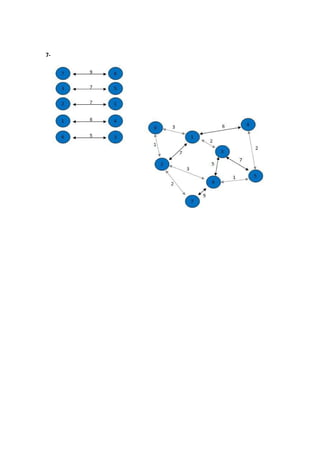
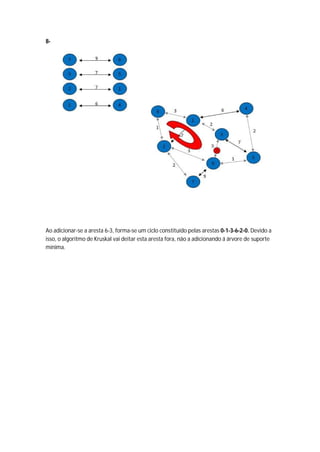
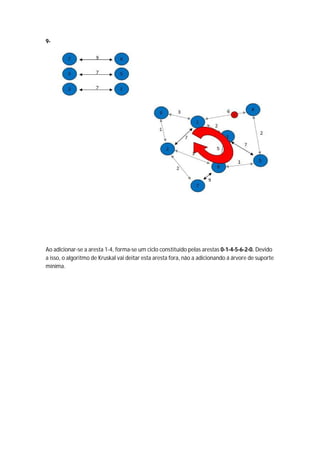
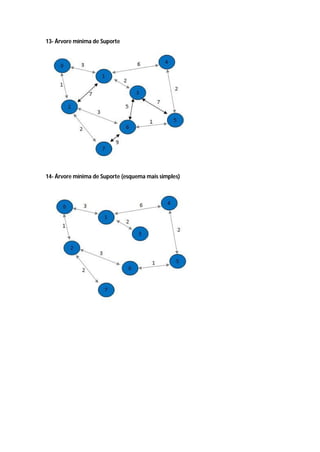
O algoritmo de Kruskal constrói a árvore geradora mínima ordenando as arestas por peso crescente e adicionando-as à árvore se não causarem ciclos, ignorando arestas que criem ciclos. Ele começa com vértices isolados e vai juntando os de menor custo até cobrir todos os vértices.

1. Algoritmo de Kruskal
O algoritmo de Kruskal. É mais um algoritmo que serve para construir a árvore de suporte
mínima. O seu funcionamento tem por base a ordenação das arestas por ordem crescente do
seu valor. A Partir da ordenação, o algoritmo começa a inserir arestas, uma a uma, á árvore de
suporte mínima, por ordem crescente do seu valor, e sempre que detecta um ciclo rejeita essa
aresta. Quando já não houver mais arestas para á árvore que o algoritmo está construído,
então a árvore de suporte mínima esta construída.
Considere o seguinte grafo.
Agora vamos fazer a ordenação das arestas do grafo por ordem crescente do seu valor numa
pilha.

3. Inicio da execução do algoritmo de Kruskal

4. 1-
Nota: As arestas a cinzento representam as arestas que pertencem á árvore mínima de
suporte em cada momento. No final o conjunto das arestas cinzentas representa a árvore
mínima de suporte.

5. 2-

6. 3-

7. 4-

8. 5-

9. 6-

10. 7-

11. 8-
Ao adicionar-se a aresta 6-3, forma-se um ciclo constituído pelas arestas 0-1-3-6-2-0. Devido a
isso, o algoritmo de Kruskal vai deitar esta aresta fora, não a adicionando á árvore de suporte
mínima.

12. 9-
Ao adicionar-se a aresta 1-4, forma-se um ciclo constituído pelas arestas 0-1-4-5-6-2-0. Devido
a isso, o algoritmo de Kruskal vai deitar esta aresta fora, não a adicionando á árvore de suporte
mínima.

13. 10-
Nota: Ao adicionar-se a aresta 2-1, forma-se um ciclo constituído pelas arestas 0-1-2-0. Devido
a isso, o algoritmo de Kruskal vai deitar esta aresta fora, não a adicionando á árvore de suporte
mínima.

14. 11-
Nota: Ao adicionar-se a aresta 3-7, formam-se dois ciclos constituídos pelas arestas 0-1-3-5-6-
2-0 e 1-4-5-3-1. Devido a isso, o algoritmo de Kruskal vai deitar esta aresta fora, não a
adicionando á árvore de suporte mínima.

15. 12-
Nota: Ao adicionar-se a aresta 7-6, forma-se um ciclo constituído pelas arestas 2-6-7-2. Devido
a isso, o algoritmo de Kruskal vai deitar esta aresta fora, não a adicionando á árvore de suporte
mínima.

16. 13- Árvore mínima de Suporte
14- Árvore mínima de Suporte (esquema mais simples)