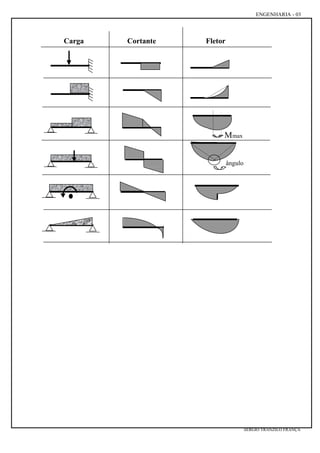
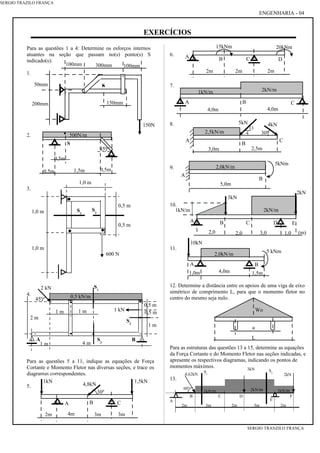
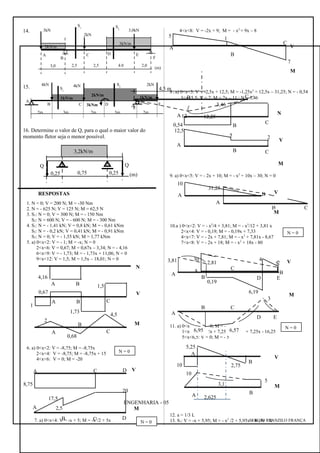
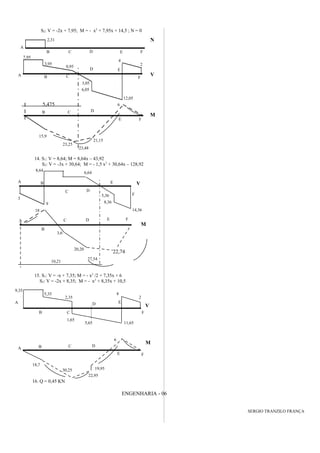
O documento apresenta resumos e exercícios sobre esforços internos em estruturas, abordando conceitos como força normal, força cortante, momento fletor e diagramas de esforços. São explicados os princípios do método das seções e apresentados exemplos de cálculo de esforços em vigas sob diversas condições de carregamento.

1. Ty
Tx
M
N
V
Força Normal
Força Cortante
Momento Fletor
B
B
AA
UNIVERSIDADE SALVADOR - UNIFACS
DEPARTAMENTO DE ENGENHARIA E ARQUITETURA
PROF.: SERGIO TRANZILLO FRANÇA
RESISTÊNCIA DOS MATERIAIS I - RESUMOS E EXERCÍCIOS COMPLEMENTARES
CURSO: ENGENHARIA
ESFORÇOS INTERNOS. Forças Internas: Força Normal; Força Cortante;
Momento Fletor; Diagramas.
Os esforços internos em uma peça serão calculados a partir do método das seções: Se a estrutura estava
em equilíbrio, cada uma das partes também estará
ESFORÇOS INTERNOS: Sistema R e MR
(em cada lado da seção)
PLANO:
Força Normal (N) – Efeito: Tração ou Compressão
Força Cortante (V) – Efeito: Deslizar as seções, perpendicularmente ao eixo.
Momento Fletor (M) – Fletir a peça (fibras tracionadas e fibras comprimidas)
BARRAS SUBMETIDAS A DUAS FORÇAS:
Força normal, igual em todas as seções.
ESTRUTURAS COM VARIAS BARRAS:
1. Calcula-se reações de apoio
2. Desmembra-se os elementos,
aplicando as forças correspondentes
nos pontos de ligação;
3. Calcula-se o equilíbrio da parte cortada,
determinando-se os esforços na seção.
VIGAS (BARRAS):
ENGENHARIA - 01
CBA
M
Resultante das
forças em AB M
V
V
N
N Resultante das
forças em BC
SERGIO TRANZILO FRANÇA
M
V
N
-F
B
F
ABA
F F-F -F
RAx
RAy
Q1
q1
M
V
N
M V
N
R
V - Cortante
N - Normal
Vy
Vz
M
M - Fletor
T - Torsor
My
Mz
Q1
Q2
RAy
RAx
q1
q2
RBy

2. ROTEIRO: 1. Calcular reações de apoio
2. Identificar pontos de transição: (carga concentrada; momento concentrada; carga
distribuída – inicio, mudança, final)
3. Cortar em cada trecho (substituir carga distribuída por resultantes parciais)
4. Indicar solicitações previstas (N, V, M)
5. Aplicar equações de equilíbrio
6. Definir as equações de variação dos esforços nos trechos
7. Representar os diagramas (convenções)
Sinais (convenções):
DIAGRAMAS DE MOMENTO FLETOR E FORÇA CORTANTE: variação de M e V em função de x.
Para cada trecho podemos determinar uma equação para a variação do Momento Fletor e da Força
Cortante.
Relação entre q, V e M:
Entre dois pontos:
CARACTERÍSTICA DOS DIAGRAMAS:
• Entre cargas concentradas: Diagrama de força cortante constante e de momento fletor reta
inclinada;
• Ponto de aplicação de carga concentrada: Diagrama de força cortante com descontinuidade e
mudança de inclinação do diagrama de momento fletor;
• Trecho com Carga distribuída: Diagrama de força cortante reta inclinada, e de momento fletor
função quadrática, com concavidade contrária a carga;
• Variação de carga distribuída: mudança de inclinação no diagrama de força cortante e
mudanção de direção da função quadrática (ângulo) no diagrama de momento fletor;
• Aplicação de Binário (momento concentrado):Descontinuidade no diagrama de momento fletor;
• Carga concentrada em trecho de carga distribuída: Descontinuidade na reta do diagrama de
força cortante, mantendo a inclinação e mudança de direção da função quadrática (ângulo) no
diagrama de momento fletor,
• Força Cortante – soma (ou subtração) da carga concentrada e da área da distribuição da carga;
• Momento Fletor: soma (ou subtração) do momento concentrado e da área do diagrama de força
cortante,
• Trecho com carga variável: diagrama de força cortante parábola quadrática e de momento fletor
parábola cúbica.
V + ∆V
M
∆x
q∆x
V
M + ∆M
M2
= M1
+ ∫ VdxV2
= V1
- ∫ qdx Para V = 0 ⇒ M máx
Inclinação de V: - q
Inclinação de M: V
= V
= -q
dV
dx
dM
dx
Carga
Força Cortante
Momento Fletor
reta horizontal
reta inclinada
parábola 2º grau
reta inclinada
parábola 2º grau
parábola 3º grau
Efeito das Forças Externas:
POSITIVO Momento FletorForça CortanteForça Normal
ENGENHARIA - 02

3. SERGIO TRANZILO FRANÇA

4. Carga Cortante Fletor
•
Mmax
ângulo
SERGIO TRANZILO FRANÇA
ENGENHARIA - 03

5. EXERCÍCIOS
Para as questões 1 a 4: Determine os esforços internos
atuantes na seção que passam no(s) ponto(s) S
indicado(s):
1.
2.
3.
4.
Para as questões 5 a 11, indique as equações de Força
Cortante e Momento Fletor nas diversas seções, e trace os
diagramas correspondentes.
5.
6.
7.
8.
9.
10.
11.
12. Determine a distância entre os apoios de uma viga de eixo
simétrico de comprimento L, para que o momento fletor no
centro do mesmo seja nulo.
Para as estruturas das questões 13 a 15, determine as equações
da Força Cortante e do Momento Fletor nas seções indicadas, e
apresente os respectivos diagramas, indicando os pontos de
momentos máximos.
13.
4,0m 4,0m
2kN/m1kN/m
A CB
5,0m
2,0kN/m
5kNm
A
B
SERGIO TRAZILO FRANÇA
4,0m
2,0kN/m
A B
1,0m 1,5m
10kN
5 kNm
2m2m
A
2m
15kNm 20kNm
B C D
2kN
(m)
3kN
1,03,02,0
2kN/m
DA B
2,0
1kN/m
C E
1,5kN1kN
4,8kN
3m3m4m2m
BA C
30º
2,5m3,0m
5kN 4kN
2,5kN/m
A
B
C
3
4 30º
2kN4,62kN
2m 3m3m 2m 2m
1kN/m 1kN/m2kN/m
3kN
S1
S2
B
A
C D
E
F
60º
ENGENHARIA - 04
L
a
Wo
SERGIO TRANZILO FRANÇA
150N
S
150mm
100mm300mm100mm
200mm
50mm
·
S
0,5m1,5m
0,5m
·
0,5m
500N/m
45º
0,5 m
0,5 m
4 m1 m
2 m
0,5 kN/m
S1
1 m
1 m
A B
1 m 1 kN
2 kN
45º
S3
S2
600 N
1,0 m
1,0 m
1,0 m
0,5 m
0,5 m
S2
S1

6. 4kN 2kN4kN
2m 3m3m 2m 2m
1kN/m
2kN/m
3kNm
S1
S2
1kN/m
A
B C D
E
F
3kN
2kN
3,0kN
3,0 2,5 4.02,5 2,0
(m)
B F
A C D E
S1 S2
2kN/m
3kN/m
14.
15.
16. Determine o valor de Q, para o qual o maior valor do
momento fletor seja o menor possível.
RESPOSTAS
1. N = 0; V = 200 N; M = -30 Nm
2. N = - 625 N; V = 125 N; M = 62,5 N
3. S1: N = 0; V = 300 N; M = - 150 Nm
S2: N = 600 N; V = - 600 N; M = - 300 Nm
4. S1: N = - 1,41 kN; V = 0,8 kN; M = - 0,61 kNm
S2: N = - 0,2 kN; V = 0,41 kN; M = - 0,91 kNm
S3: N = 0; V = - 1,55 kN; M = 1,77 kNm
5. a) 0<x<2: V = - 1; M = -x; N = 0
2<x<6: V = 0,67; M = 0,67x – 3,34; N = - 4,16
6<x<9: V = - 1,73; M = - 1,73x + 11,06; N = 0
9<x<12: V = 1,5; M = 1,5x – 18,01; N = 0
6. a) 0<x<2: V = -8,75; M = -8,75x
2<x<4: V = -8,75; M = -8,75x + 15
4<x<6: V = 0; M = -20
7. a) 0<x<4: V = -x + 5; M = -x2
/2 + 5x
4<x<8: V = -2x + 9; M = - x2
+ 9x – 8
8.a) 0<x<3: V = -2,5x + 12,5; M = -1,25x2
+ 12,5x – 31,25; N = - 0,54
3<x<5,5: V = 2; M = 2x – 11 ; N = 3,46
9. a) 0<x<5: V = - 2x + 10; M = - x2
+ 10x – 30; N = 0
10.a ) 0<x<2: V = - x2
/4 + 3,81; M = - x3
/12 + 3,81 x
2<x<4: V = - 0,19; M = - 0,19x + 7,33
4<x<7: V = - 2x + 7,81; M = - x2
+ 7,81x - 8,67
7<x<8: V = - 2x + 18; M = - x2
+ 18x - 80
11. a) 0<x<1: V = -10; M = - 10x
1<x<5: V = -2x + 7,25; M = - x2
+ 7,25x - 16,25
5<x<6,5: V = 0; M = - 5
12. a = 1/3 L
13. S1: V = -x + 5,95; M = - x2
/2 + 5,95x + 6 ; N = 0
(m)0,250,750,25
QQ
3,2kN/m
ENGENHARIA - 05
1,73
1,5
0,67
1
CA B
N
0,68
4,5
2
CA
B
V
M
N = 0
8,75
A C D
20
2,5
17,5
A
C DB
V
M
N = 0
A
C
B
5
7
1
V
M
N
0,54
A
B
C
3,46
V
M
12,5
A
B C
25
10
A B
31,25
A
B C
5V
M
N = 0
5
30
A B
V
6,19
0,19
3,81
D
A
B
2,81
C
E
2
4
M
N = 0
A
CB
12,2512
4,5 m
6,576,95
3
D
A
B C
E
SERGIO TRANZILO FRANÇA
4,16
A B
5,25
A
B
10 2,75
V
5
A B
10
M
2,625
3,1

7. FE
30,25
S2: V = -2x + 7,95; M = - x2
+ 7,95x + 14,5 ; N = 0
14. S1: V = 8,64; M = 8,64x – 43,92
S2: V = -3x + 30,64; M = - 1,5 x2
+ 30,64x – 128,92
15. S1: V = -x + 7,35; M = - x2
/2 + 7,35x + 6
S2: V = -2x + 8,35; M = - x2
+ 8,35x + 10,5
16. Q = 0,45 KN
22,74
27,54
18
20,20
3,6
B
A C D
10,21
M
V
5,35
1,65
2,35
5,65
9,35
A
B C
D E
F
11,65
4
2
V
M
ENGENHARIA - 06
SERGIO TRANZILO FRANÇA
22,95
6
18,7
A B C D
E F
19,95
2,31
M
3,95
3,05
7,95
0,95
B C
D E
F
6,05
12,05
2
4
V
N
F
B
A
C D E F
A
5,475
23,25
23,48
6
B C D
E
21,15
15,9
5,36
8,64
6,64
3
8,369
B
F
A
C D
E
14,36