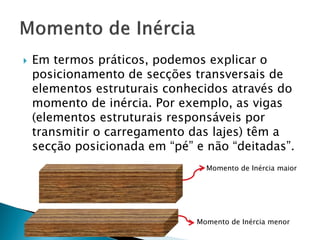
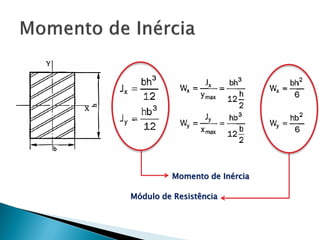
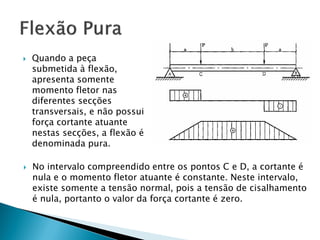
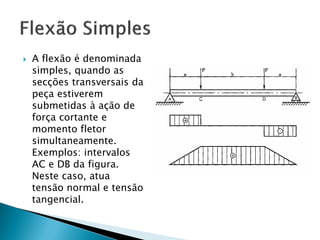
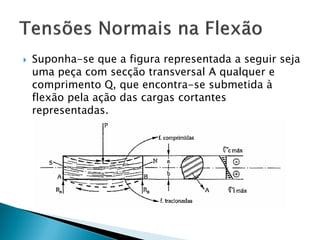
O documento discute conceitos importantes de resistência dos materiais relacionados à estabilidade de elementos estruturais, como: 1) momento de inércia, que fornece uma medida da resistência à flexão de uma seção; 2) como vigas são projetadas com seções na posição vertical para maximizar o momento de inércia; 3) os tipos de flexão em elementos estruturais.

1. Resistência dos Materiais - Estabilidade

2.  O momento de inércia é uma característica
geométrica importantíssima no
dimensionamento dos elementos de
construção, pois fornece através de valores
numéricos, uma noção de resistência da peça.
 Quanto maior for o momento de inércia da
secção transversal de uma peça, maior será a
resistência da peça.

3.  Em termos práticos, podemos explicar o
posicionamento de secções transversais de
elementos estruturais conhecidos através do
momento de inércia. Por exemplo, as vigas
(elementos estruturais responsáveis por
transmitir o carregamento das lajes) têm a
secção posicionada em “pé” e não “deitadas”.
Momento de Inércia maior
Momento de Inércia menor

4.  O momento de inércia da secção retangular
(comum em vigas) disposta em “pé” é muito
maior, o que diminui as tensões na flexão e a
deformação. Para melhor entender este
conceito, tente flexionar uma régua comum
com a secção deitada e depois em pé.
Percebe-se que é muito mais fácil dobrar ou
flexionar a régua quando e mesma está
deitada, isso por que o momento de inércia é
menor.

5. Momento de Inércia
Módulo de Resistência

6.  Quando a peça
submetida à flexão,
apresenta somente
momento fletor nas
diferentes secções
transversais, e não possui
força cortante atuante
nestas secções, a flexão é
denominada pura.
 No intervalo compreendido entre os pontos C e D, a cortante é
nula e o momento fletor atuante é constante. Neste intervalo,
existe somente a tensão normal, pois a tensão de cisalhamento
é nula, portanto o valor da força cortante é zero.

7.  A flexão é denominada
simples, quando as
secções transversais da
peça estiverem
submetidas à ação de
força cortante e
momento fletor
simultaneamente.
Exemplos: intervalos
AC e DB da figura.
Neste caso, atua
tensão normal e tensão
tangencial.

8.  Suponha-se que a figura representada a seguir seja
uma peça com secção transversal A qualquer e
comprimento Q, que encontra-se submetida à
flexão pela ação das cargas cortantes
representadas.

9.  As fibras inferiores da peça encontram-se
tracionadas, enquanto as fibras superiores se
encontram comprimidas.
 A tensão normal atuante máxima, também
denominada tensão de flexão, é determinada em
relação à fibra mais distante da seção transversal,
através da relação entre o produto do momento
fletor atuante e a distância entre a linha neutra e a
fibra, e o momento de inércia baricêntrico da
secção.

10.  Tem-se, então:
Onde:
 σc - tensão máxima nas fibras comprimidas. Como se convenciona o
momento fletor nas fibras comprimidas negativo, σc será sempre <
0 (negativo).
 σt - tensão máxima nas fibras tracionadas. Como, por convenção, o
momento fletor é positivo nas fibras tracionadas, σt será sempre > 0
(positivo).

11.  Para o dimensionamento das peças
submetidas a esforço de flexão, utiliza-se a
tensão admissível, que será a tensão atuante
máxima na fibra mais afastada, não
importando se a fibra estiver tracionada ou
comprimida.

12.  Tem-se então:
 Como
 Portanto