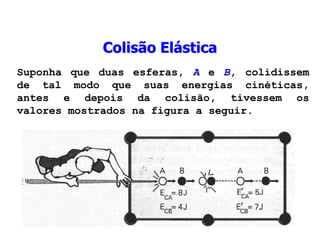
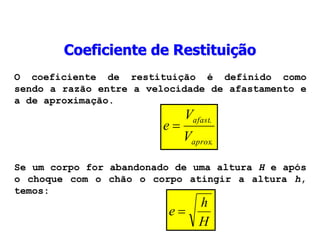
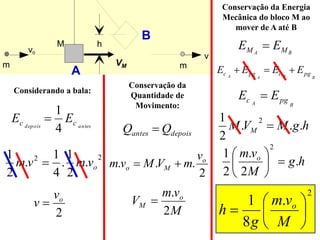
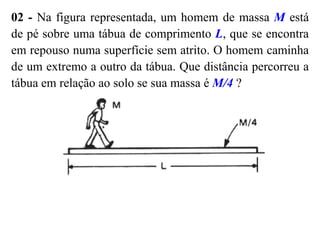
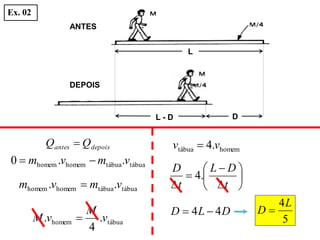
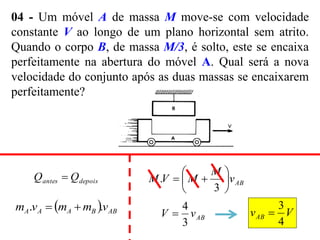
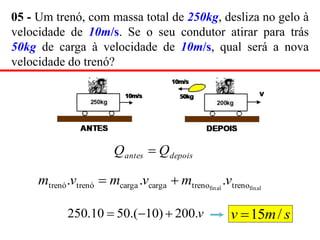
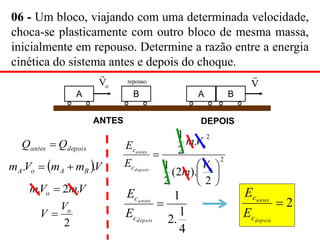
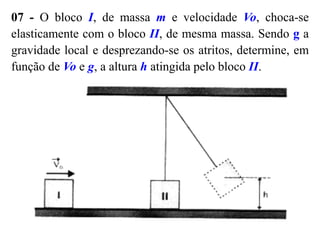
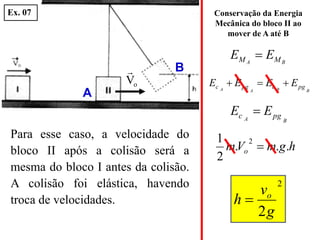
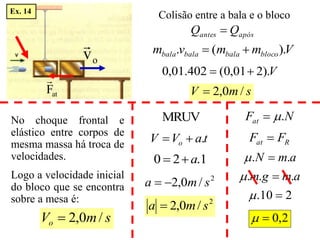
1) O documento aborda os conceitos de impulso, quantidade de movimento, teorema do impulso, sistemas isolados de forças, conservação da quantidade de movimento e tipos de colisões. 2) São apresentadas as definições matemáticas de impulso e quantidade de movimento e discutidos exemplos de sua aplicação. 3) São explicados os princípios da conservação da quantidade de movimento e da energia mecânica durante colisões elásticas e inelásticas.

1. FÍSICA A
Colisões

2.  Impulso
 Quantidade de Movimento
 Teorema do Impulso
 Sistema Isolado de Forças
 Princípio da Conservação da
Quantidade de Movimento
 Colisões
ASSUNTOS ABORDADOS

3. Impulso
É a grandeza física vetorial relacionada com a
força aplicada em um corpo durante um intervalo
de tempo.
O impulso é dado pela expressão:
t
F
I 
 .


I = impulso (N.s);
F = força (N);
t = tempo de atuação da força F (s).

4. v
O Impulso é uma grandeza vetorial que possui a
mesma direção e sentido da força aplicada.
Ao empurrarmos um carro, por exemplo, quanto
maior a intensidade da força e o tempo de atuação
dessa força, maior será o impulso aplicado no
carro.
t
F
I 
 .


Impulso

5. Canhões de longo alcance possuem canos compridos.
Quanto mais longo este for, maior a velocidade
emergente da bala.
Isso ocorre porque a força gerada pela explosão
da pólvora atua no cano longo do canhão por um
tempo mais prolongado. Isso aumenta o impulso
aplicado na bala do canhão.
O mesmo ocorre com os rifles em relação aos
revólveres.
Impulso

6. Quando a força aplicada não for constante ao
longo do tempo, a intensidade do impulso pode ser
calculada através da Área do gráfico F x t com o
eixo do tempo, conforme a seguir.
|F|
t
A
t1 t2
I = Área
Impulso

 dt
F
I .

7. Quantidade de Movimento
Todos nós sabemos que é muito mais
difícil parar um caminhão pesado do que
um carro que esteja se movendo com a
mesma rapidez.
Isso se deve ao fato do caminhão ter
mais inércia em movimento, ou seja,
quantidade de movimento.

8. Quantidade de Movimento
É a grandeza física vetorial relacionada com a
massa de um corpo e sua velocidade.
A quantidade de movimento, ou momento linear, é
dada pela expressão:
Q = quantidade de movimento (kg.m/s);
m = massa (kg);
v = velocidade (m/s).
v
m
Q


.


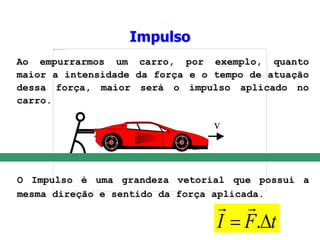
9. A quantidade de movimento é uma grandeza vetorial
que possui a mesma direção e sentido da
velocidade.
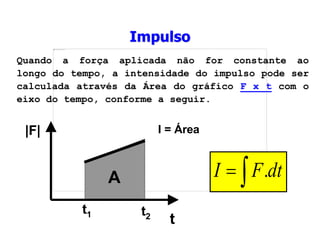
As unidades (dimensões) de Impulso e Quantidade
de Movimento são equivalentes:
Quantidade de Movimento
]
[
/
.
.
.
.
]
[ 2
Q
s
m
kg
s
s
m
kg
s
N
I 




10. Teorema do Impulso
Considere um corpo de massa m que se desloca em
uma superfície horizontal com uma velocidade vo. Em
um certo instante passa a atuar nele uma força
resultante de intensidade F, durante um intervalo
de tempo t.
O impulso produzido pela força F é igual a:
Q
I




t
F
I 
 .
o
V
m
V
m
I .
. 

a
m
F .
 t
a
m
I 
 .
.
t
V
V
a o


 t
t
V
V
m
I o









 .
.  
o
V
V
m
I 
 .
v
m
Q .


11. Para o mesmo intervalo de tempo, o
impulso da força resultante é igual à
variação da quantidade de movimento.
Q
I




Teorema do Impulso

12. Sistema Isolado de Forças
Considere um sistema formado por dois corpos A e
B que se colidem.
No sistema, as forças decorrentes de agentes
externos ao sistema são chamadas de forças
externas, como, por exemplo o peso P e a normal
N. No sistema, a resultante dessas forças
externas é nula.

13. Durante a interação, o corpo A exerce uma força F
no corpo B e este exerce no corpo B uma força -F,
de mesmo módulo e sentido oposto. As forças F e
-F correspondem ao par Ação e Reação.
Denomina-se sistema isolado de forças externas
o sistema cuja resultante dessas forças é nula,
atuando nele somente as forças internas.
Sistema Isolado de Forças

14. Princípio da Conservação da
Quantidade de Movimento
Pelo Teorema do Impulso
A quantidade de movimento de um sistema
de corpos, isolado de forças externas, é
constante.
Como
Considerando um sistema isolado de forças
externas:
0

R
F t
F
I R 
 . 0

I
I
F Q
Q
I 

0

I F
I Q
Q 
F
I Q
Q 

15. A quantidade de movimento pode permanecer
constante ainda que a energia mecânica
varie. Isto é, os princípios da conservação
de energia e da quantidade de movimento são
independentes.
A quantidade de movimento dos corpos que
constituem o sistema mecanicamente isolado
não é necessariamente constante. O que
permanece constante é a quantidade de
movimento total dos sistema.
Observações

16. Durante uma desfragmentação ou explosão o
centro de massa do sistema não altera o seu
comportamento.
Observações

17. As colisões podem ocorrer de duas maneiras
distintas, dependendo do que ocorre com a
energia cinética do sistema antes e depois da
colisão.
1 - Colisão Elástica
2 - Colisão Inelástica
Colisões

18. Colisão Elástica
Suponha que duas esferas, A e B, colidissem
de tal modo que suas energias cinéticas,
antes e depois da colisão, tivessem os
valores mostrados na figura a seguir.

19. Observe que, se calcularmos a energia cinética
total do sistema, encontraremos:
Antes da Colisão: EcA + EcB = 8+4 = 12j
Após a Colisão: EcA + EcB = 5+7 = 12j
Neste caso, a energia cinética total dos corpos
que colidiram se conservou. Esse tipo de colisão,
na qual, além da conservação de movimento (que
sempre ocorre), há também a conservação da
energia cinética, é denominada colisão elástica.
Colisão Elástica

20. Colisão Inelástica (ou Plástica)
É aquela onde a energia cinética não se
conserva. Isso ocorre porque parte da energia
cinética das partículas envolvidas no choque
se transforma em energia térmica, sonora etc.
Não se esqueça, mesmo a energia cinética não
se conservando, a quantidade de movimento do
sistema se conserva durante a colisão.
A maioria das colisões que ocorrem na
natureza é inelástica.

21. Colisão Perfeitamente Inelástica
É aquela que, após o choque, os corpos passam a
ter a mesma velocidade (movem-se juntos), tendo a
maior perda possível de energia cinética do
sistema.
A figura a seguir exemplifica um colisão
perfeitamente inelástica.
Obs.: na colisão perfeitamente inelástica não se
perde, necessariamente, toda a energia cinética.

22. O coeficiente de restituição é definido como
sendo a razão entre a velocidade de afastamento e
a de aproximação.
.
.
aprox
afast
V
V
e 
Se um corpo for abandonado de uma altura H e após
o choque com o chão o corpo atingir a altura h,
temos:
H
h
e 
Coeficiente de Restituição

23. O coeficiente de restituição é um número puro
(grandeza adimensional), extremamente útil na
classificação e equacionamento de uma colisão:
Colisão Elástica vafast. = vaprox. e = 1
Colisão Inelástica vafast. < vaprox 0 < e < 1
Colisão Perf. Inelástica vafast. = 0 e = 0
Coeficiente de Restituição

24. LEMBRE-SE QUE
 O impulso é uma grandeza vetorial relacionada
com uma força e o tempo de atuação da mesma.
 Quantidade de movimento é uma grandeza vetorial
que possui mesma direção e sentido do vetor
velocidade.
 O impulso corresponde à variação da quantidade
de movimento.
 Durante uma colisão (ou explosão) a quantidade
de movimento do sistema permanece constante.
 A quantidade de movimento pode permanecer
constante ainda que a energia mecânica varie.
 Após a colisão perfeitamente inelástica os
corpos saem juntos.

25. Exemplos

26. A figura mostra dois blocos, A e B, em repouso, encostados em
uma mola comprimida, de massa desprezível. Os blocos estão
apoiados em uma superfície sem atrito e sua massas são 5,0kg e
7,0kg, respectivamente. Supondo que o bloco B adquira uma
velocidade de 2,0m/s, qual a velocidade adquirida pelo bloco A?
depois
antes Q
Q 
B
B
A
A v
m
v
m .
.
0 

)
2
.(
7
.
5
0 

 A
v
s
m
vA /
8
,
2


27. Despreze todas as formas de atrito e considere que:
a - inicialmente, o conjunto se encontra em repouso;
b - m2 = 4 m1;
c - o corpo de massa m1 é lançado horizontalmente
para a esquerda, com velocidade de 12m/s.
Tendo em vista o que foi apresentado, qual será a velocidade
de lançamento do bloco m2?
depois
antes Q
Q 
2
2
1
1 .
.
0 v
m
v
m 

2
1
1 .
4
)
12
.(
0 v
m
m 


s
m
v /
0
,
3
2 

28. Um automóvel de 1,0 tonelada colidiu frontalmente com um
caminhão de 9,0 toneladas. A velocidade do automóvel era de
80km/h para a direita e a do caminhão, de 40km/h para a
esquerda. Após a colisão, os dois veículos permaneceram juntos.
1 - DETERMINE a velocidade do conjunto caminhão e
automóvel logo após a colisão.
2 - RESPONDA se, em módulo, a força devido à colisão que
atuou sobre o automóvel é maior, menor ou igual à aquela que
atuou sobre o caminhão. JUSTIFIQUE sua resposta.
V = 28 km/h, para a esquerda
IGUAL
Ação e Reação
depois
antes Q
Q 
2
2
1
1
2
2
1
1 ´
.
´
.
.
. v
m
v
m
v
m
v
m 


V
).
9
1
(
)
40
.(
9
80
.
1 



h
km
V /
28



29. Uma bala de massa m e velocidade Vo atravessa, quase
instantaneamente, um bloco de massa M, que se encontrava
em repouso, pendurado por um fio flexível, de massa
desprezível. Nessa colisão a bala perde ¾ de sua energia
cinética inicial. Determine a altura h, alcançada pelo
pêndulo.
h
vo
v
m
M
m

30. h
vo
v
m
M
m
2
.
.
. o
M
o
v
m
V
M
v
m 

depois
antes Q
Q 
B
A M
M E
E 
h
g
M
V
M M .
.
.
2
1 2

A
B
2
.
8
1







M
v
m
g
h o
antes
depois c
c E
E
4
1

2
2
.
2
1
.
4
1
.
2
1
o
v
m
v
m 
2
o
v
v 
M
v
m
V o
M
2
.

VM
B
B
A
A pg
c
pg
c E
E
E
E 


Considerando a bala:
Conservação da
Quantidade de
Movimento:
Conservação da Energia
Mecânica do bloco M ao
mover de A até B
h
g
M
v
m o
.
2
.
2
1
2







B
A pg
c E
E 

31. 01 - Um corpo de 80kg cai da altura de 80m e, após bater
no solo, retorna, atingindo a altura máxima de 20m. Qual o
valor do coeficiente de restituição entre o corpo e o solo?
H
h
e 
80
20

e
4
1

e 50
,
0

e
Exercícios

32. 02 - Na figura representada, um homem de massa M está
de pé sobre uma tábua de comprimento L, que se encontra
em repouso numa superfície sem atrito. O homem caminha
de um extremo a outro da tábua. Que distância percorreu a
tábua em relação ao solo se sua massa é M/4 ?

33. L
ANTES
DEPOIS
depois
antes Q
Q 
tábua
tábua
homem
homem
tábua
tábua
homem
homem
.
.
.
.
0
v
m
v
m
v
m
v
m



D
L
D 4
4 

D
L - D
tábua
homem .
4
. v
M
v
M 
homem
tábua .
4 v
v 









 t
D
L
t
D
.
4
5
4L
D 
Ex. 02

34. 03 - No esquema a seguir, mA=1,0kg e mB=2,0kg. Não há
atrito entre os corpos e o plano de apoio. A mola tem massa
desprezível. Estando a mola comprimida entre os blocos, o
sistema é abandonado em repouso. A mola distende-se e cai
por não estar presa a nenhum deles. O corpo B adquire
velocidade de 0,5m/s. Determine a energia potencial da
mola no instante em que o sistema é abandonado
livremente.
depois
antes Q
Q 
j
Ep 75
,
0

B
B
A
A v
m
v
m .
.
0 

5
,
0
.
2
.
1
0 
 A
v
s
m
vA 0
,
1


B
A c
c
p E
E
E 

2
2
.
2
1
.
2
1
B
B
A
A
p v
m
v
m
E 

2
2
5
,
0
.
2
2
1
)
1
.(
1
.
2
1



p
E

35. 04 - Um móvel A de massa M move-se com velocidade
constante V ao longo de um plano horizontal sem atrito.
Quando o corpo B, de massa M/3, é solto, este se encaixa
perfeitamente na abertura do móvel A. Qual será a nova
velocidade do conjunto após as duas massas se encaixarem
perfeitamente?
depois
antes Q
Q 
  AB
B
A
A
A v
m
m
v
m .
. 

AB
v
M
M
V
M 







3
.
AB
v
V
3
4
 V
vAB
4
3


36. 05 - Um trenó, com massa total de 250kg, desliza no gelo à
velocidade de 10m/s. Se o seu condutor atirar para trás
50kg de carga à velocidade de 10m/s, qual será a nova
velocidade do trenó?
depois
antes Q
Q 
final
final treno
treno
carga
carga
trenó
trenó .
.
. v
m
v
m
v
m 

v
.
200
)
10
.(
50
10
.
250 

 s
m
v /
15


37. 06 - Um bloco, viajando com uma determinada velocidade,
choca-se plasticamente com outro bloco de mesma massa,
inicialmente em repouso. Determine a razão entre a energia
cinética do sistema antes e depois do choque.
depois
antes Q
Q 
 V
m
m
V
m B
A
o
A .
. 

A
ANTES
o
V

B
repouso
DEPOIS
B
V

A
V
m
V
m o .
2
. 
2
o
V
V 
2
2
2
).
2
(
2
1
.
2
1







o
o
c
c
V
m
V
m
E
E
depois
antes
2

depois
antes
c
c
E
E
4
1
.
2
1

depois
antes
c
c
E
E

38. 07 - O bloco I, de massa m e velocidade Vo, choca-se
elasticamente com o bloco II, de mesma massa. Sendo g a
gravidade local e desprezando-se os atritos, determine, em
função de Vo e g, a altura h atingida pelo bloco II.

39. B
A M
M E
E 
h
g
m
V
m o .
.
.
2
1 2

2
2g
v
h o

B
B
A
A pg
c
pg
c E
E
E
E 


Conservação da Energia
Mecânica do bloco II ao
mover de A até B
B
A pg
c E
E 
o
V

Para esse caso, a velocidade do
bloco II após a colisão será a
mesma do bloco I antes da colisão.
A colisão foi elástica, havendo
troca de velocidades.
A
B
Ex. 07

40. 08 - Um pequeno vagão, de massa 90kg, rola à velocidade
de 10m/s, sobre um trilho horizontal. Num determinado
instante cai verticalmente, de uma correia transportadora,
sobre o vagão, um saco de areia de 60kg. Determine a
velocidade do vagão carregado.
depois
antes Q
Q  v
).
60
90
(
10
.
90 
 s
m
v /
0
,
6


41. 09 - A quantidade de movimento de uma partícula de massa
0,4kg tem módulo 1,2kg.m/s. Neste instante, qual a energia
cinética da partícula é, em joules?
2
.
2
1
v
m
Ec 
j
Ec 8
,
1

v
m
Q .

m
Q
v 
2
.
2
1







m
Q
m
Ec
m
Q
Ec
2
2

4
,
0
.
2
2
,
1 2

c
E

42. 10 - Um carro de corrida de massa 800kg entra numa curva
com velocidade 30m/s e sai com velocidade de igual
módulo, porém numa direção perpendicular à inicial, tendo
sua velocidade sofrido uma rotação de 90°. Determine a
intensidade do impulso recebido pelo carro.
Q
I



 v
m
I



 .
v

o
v


v


2
2
2
v
v
v o 


2
2
2
30
30 

v
s
m
v 2
30


v
m
I



 . 2
30
.
800

I s
N
I .
10
.
39
,
3 4


43. 11 - Uma esfera de massa m e velocidade v colidiu
frontalmente com um obstáculo fixo, retornando com a
mesma velocidade em módulo. Qual foi a variação da
quantidade de movimento da esfera?
v
m
Q




 .
))
(
.( v
v
m
Q 



v
m
Q .
2


v
m
Q


.

m
v

ANTES
m
v

DEPOIS

44. 12 - Uma bala de 0,20kg tem
velocidade horizontal de 300m/s;
bate e fica presa num bloco de
madeira de massa 1,0kg, que estão
em repouso num plano horizontal,
sem atrito. Determine a velocidade
com que o conjunto (bloco e bala)
começa a deslocar-se.
depois
antes Q
Q  v
.
2
,
1
300
.
2
,
0  s
m
v /
50


45. 13 - Em um plano horizontal sem atrito, duas partículas, A
e B, realizam uma colisão unidimensional. Não considere o
efeito do ar. A partícula A tem massa m e a partícula B tem
massa M. Antes da colisão a partícula B estava em repouso
e após a colisão a partícula A fica em repouso. Qual o
coeficiente de restituição nesta colisão?
após
antes Q
Q 
B
B
A
A v
m
v
m .
. 
M
m
e 
.
. .
. afast
aprox v
M
v
m 
.
.
aprox
afast
v
v
e 

46. 14 - Um pêndulo balístico de massa 2kg, atingido por um
projétil de massa 10g com velocidade 402m/s, colide
frontal e elasticamente com um bloco de massa 2,01kg.
Após a colisão, o bloco desliza, sobre uma mesa, parando
em 1,0s. Considerando g = 10m/s², determine o coeficiente
de atrito entre a mesa e o bloco. Considere que o projétil se
aloja no pêndulo.

47. após
antes Q
Q 
Colisão entre a bala e o bloco
V
m
m
v
m bloco
bala
bala
bala ).
(
. 

V
).
2
01
,
0
(
402
.
01
,
0 

s
m
V /
0
,
2

s
m
Vo /
0
,
2

No choque frontal e
elástico entre corpos de
mesma massa há troca de
velocidades.
Logo a velocidade inicial
do bloco que se encontra
sobre a mesa é:
t
a
V
V o .


1
.
2
0 a


2
/
0
,
2 s
m
a 

N
Fat .


R
at F
F 
a
m
N .
. 

a
m
g
m .
.
. 

2
10
. 

2
,
0


2
/
0
,
2 s
m
a 
o
v

MRUV
at
F

Ex. 14