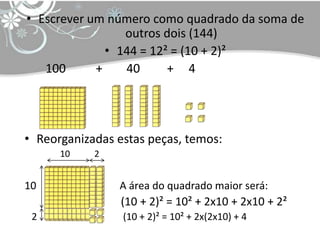
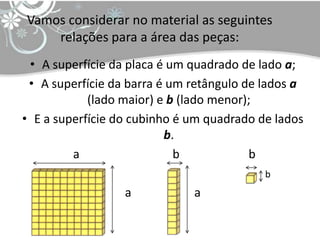
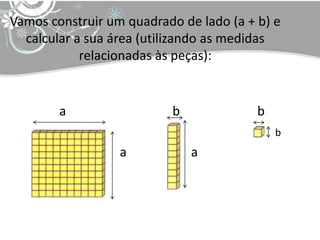
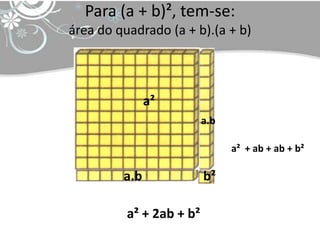
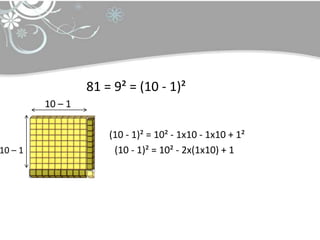
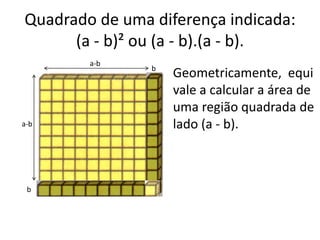
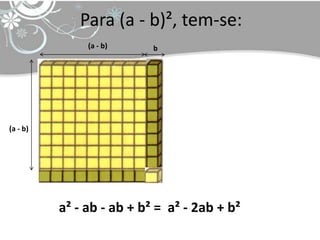
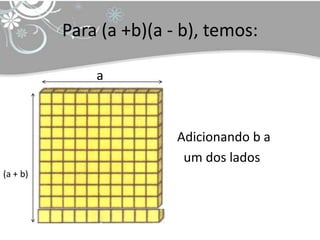
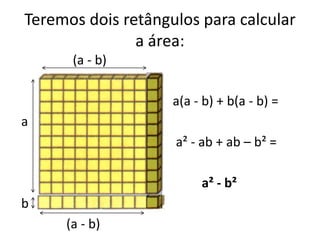
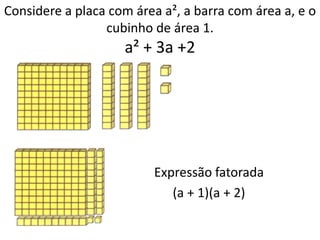
O documento discute tópicos em educação matemática como álgebra, desenvolvimento da capacidade operacional de acordo com Piaget e capacitação de professores. Apresenta exemplos de expressões algébricas como fatoração de números e cálculo de áreas de figuras geométricas. Finaliza citando referências bibliográficas sobre o tema.

1. UNIVERSIDADE ESTADUAL DO CENTRO-OESTE – UNICENTRO
Campus CEDETEG
Setor de Ciências Exatas e de Tecnologia
Tópicos em Educação Matemática
Guarapuava
Junho - 2012

3. • Álgebra e definições;
• Piaget: desenvolvimento da capacidade de
operacionalizar a partir de um objeto com
exemplares concretos;
• Capacitação do professor;

4. Operatório formal

6. • Escrever um número como quadrado da soma de
outros dois (144)
• 144 = 12² = (10 + 2)²
100 + 40 + 4
• Reorganizadas estas peças, temos:
10 2
10 A área do quadrado maior será:
(10 + 2)² = 10² + 2x10 + 2x10 + 2²
2 (10 + 2)² = 10² + 2x(2x10) + 4

7. Vamos considerar no material as seguintes
relações para a área das peças:
• A superfície da placa é um quadrado de lado a;
• A superfície da barra é um retângulo de lados a
(lado maior) e b (lado menor);
• E a superfície do cubinho é um quadrado de lados
b.
a b b
b
a a

8. Vamos construir um quadrado de lado (a + b) e
calcular a sua área (utilizando as medidas
relacionadas às peças):
a b b
b
a a

9. Para (a + b)², tem-se:
área do quadrado (a + b).(a + b)
a²
a.b
a² + ab + ab + b²
a.b b²
a² + 2ab + b²

11. 81 = 9² = (10 - 1)²
10 – 1
(10 - 1)² = 10² - 1x10 - 1x10 + 1²
10 – 1 (10 - 1)² = 10² - 2x(1x10) + 1

12.  Quadrado de uma diferença
indicada: (a - b)² ou (a - b).(a - b).
Geometricamente, equivale a calcular
a área de uma região quadrada de
lado (a - b).

13. Quadrado de uma diferença indicada:
(a - b)² ou (a - b).(a - b).
a-b
b
Geometricamente, equi
vale a calcular a área de
uma região quadrada de
a-b lado (a - b).
b

14. Para (a - b)², tem-se:
(a - b) b
(a - b)
a²
a² - ab - ab + b² = a² - 2ab + b²

15. Para (a +b)(a - b), temos:
a
Adicionando b a
um dos lados
(a + b)

16. Teremos dois retângulos para calcular
a área:
(a - b)
a(a - b) + b(a - b) =
a
a² - ab + ab – b² =
a² - b²
b
(a - b)

18. Considere a placa com área a², a barra com área a, e o
cubinho de área 1.
a² + 3a +2
Expressão fatorada
(a + 1)(a + 2)

19. • BRASIL, Secretaria de educação fundamental. Parâmetros
Curriculares Nacionais: matemática. Brasília: MEC/SEF, 1998;
• MODANEZ, Leila. Das sequências de padrões geométricos à
introdução ao pensamento algébrico. Dissertação
(Mestrado). São Paulo: PUC, 2003;
• PINTO, Antônio Henrique. As concepções de álgebra e
educação algébrica dos professores de atemática.
Dissertação (Mestrado). Vitória: UFES, 1999.