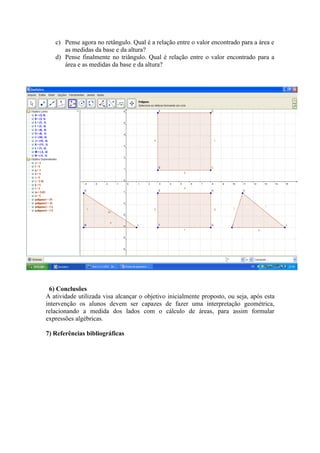
Este documento descreve uma atividade didática para ensinar áreas de polígonos para alunos de 5a a 7a série utilizando o software GeoGebra. Os alunos irão construir e medir áreas de quadrados, retângulos e triângulos para identificar as relações entre as medidas dos lados e o cálculo das áreas.

1. PUC Minas-Betim
Informática e Educação
Data: 25/11/2009
Ensino de geometria utilizando GeoGebra
Área de polígonos
Alunos: Jéssica Cristina
Joardson Junio
Luiz Fernando
Francisco Padilha
1) Tema: Área de polígonos.
2) Público alvo: Estudantes das 5ª, 6ª e 7ª séries (6º, 7º e 8º anos) do Ensino
Fundamental.
3) Objetivo: Fazer com que os alunos obtenham uma expressão algébrica para a área de
polígonos em função da medida de seus lados diante de uma interpretação geométrica.
4) Recursos didáticos utilizados
Uso do software educativo GeoGebra.
5) Metodologia
A aula será dada através dos seguintes passos, que serão feitos no GeoGebra:
1º passo:
Vá em exibir malha e construa um quadrado usando a opção polígonos regulares (de 5
unidades, por exemplo). Depois conte os quadradinhos e verifique o valor da área
fornecida na parte esquerda.
2º passo:
Construa agora, sem apagar o quadrado um retângulo usando a opção polígonos (de
base 5 unidades e altura 3 unidades, por exemplo). Depois conte os quadradinhos e
confira o valor da área.
3º passo:
Construa um triângulo que possua a mesma base e mesma altura do retângulo, sem
apagar as figuras anteriores (base 5 e altura 3 unidades, por exemplo). Conte os
quadradinhos.
4º passo:
Identifique a base e a altura dos polígonos desenhados.
Feito isto, responda:
a) A partir das medidas das bases e das alturas dos polígonos, é possível construir
uma relação numérica para essas áreas?
b) Pense inicialmente no quadrado. Qual é a relação entre o valor encontrado para a
área e a medida do lado?

2. c) Pense agora no retângulo. Qual é a relação entre o valor encontrado para a área e
as medidas da base e da altura?
d) Pense finalmente no triângulo. Qual é relação entre o valor encontrado para a
área e as medidas da base e da altura?
6) Conclusões
A atividade utilizada visa alcançar o objetivo inicialmente proposto, ou seja, após esta
intervenção os alunos devem ser capazes de fazer uma interpretação geométrica,
relacionando a medida dos lados com o cálculo de áreas, para assim formular
expressões algébricas.
7) Referências bibliográficas