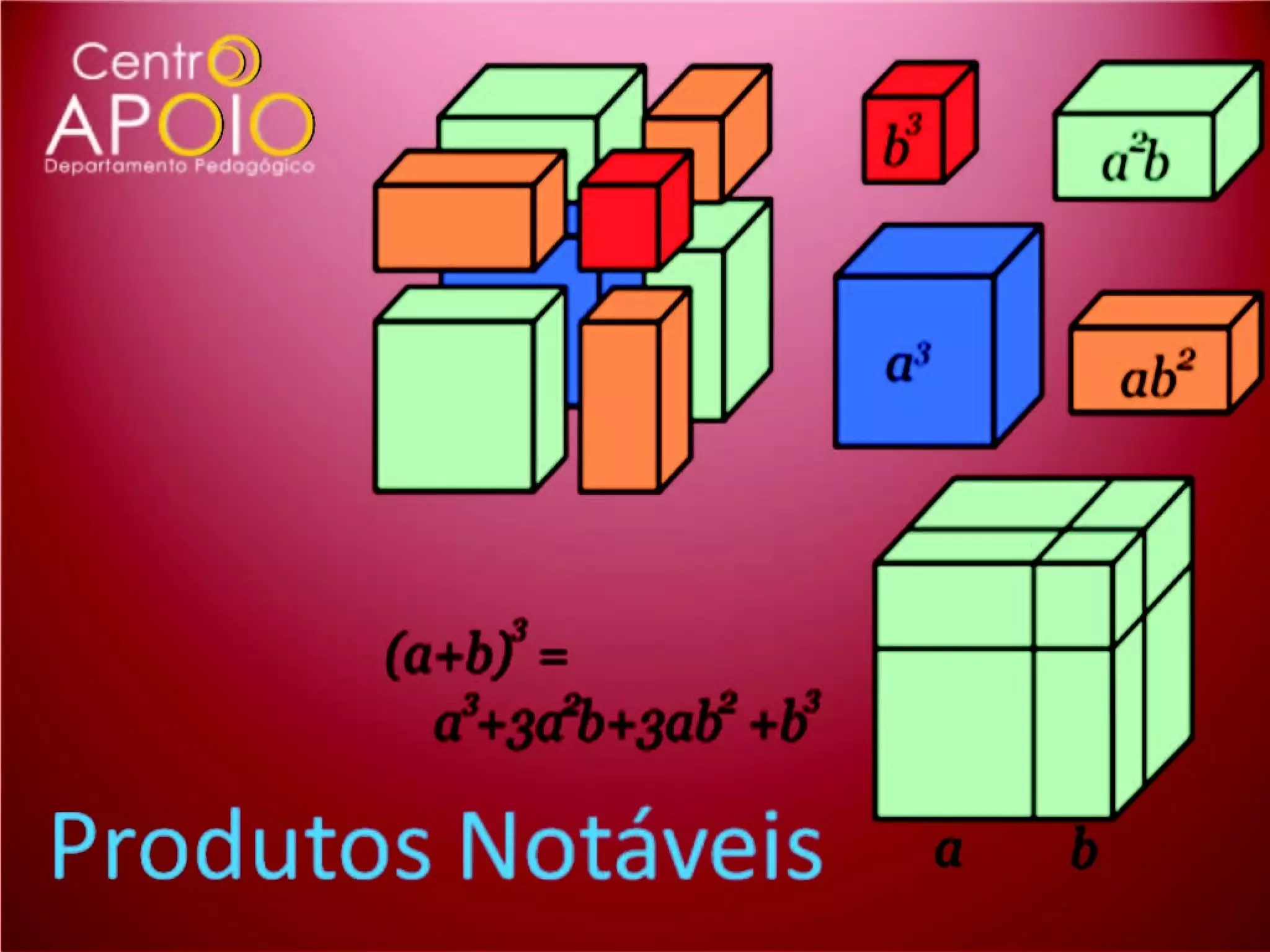
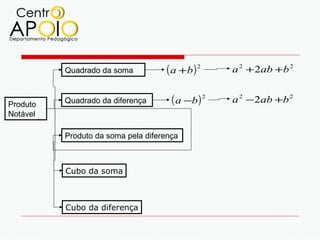
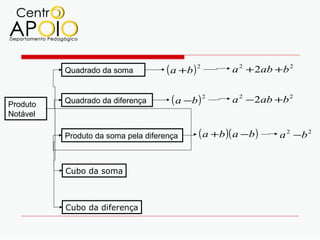
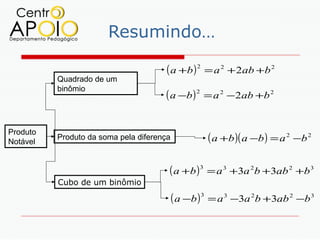
O documento explora o conceito de produtos notáveis, incluindo fórmulas como o quadrado da soma, quadrado da diferença e cubos de soma e diferença. Ele apresenta explicações e cálculos relacionados a esses produtos notáveis, ilustrando exemplos e suas aplicações. Os principais temas abordam a expansão e simplificação de expressões algébricas relacionadas a esses conceitos.