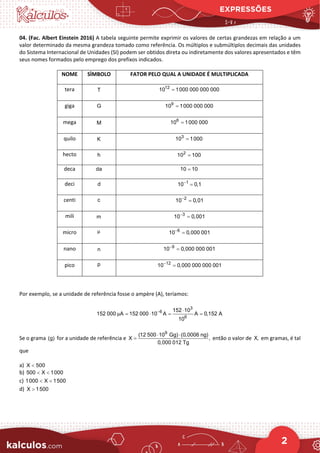
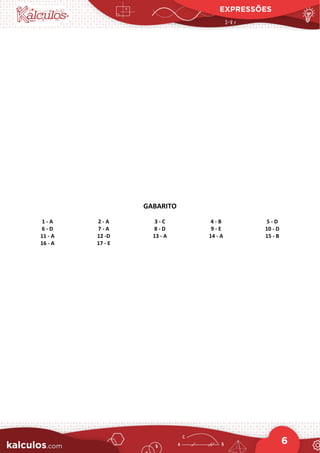
1. O documento apresenta uma lista de 17 questões de múltipla escolha sobre expressões matemáticas, potenciação, radiciação e operações com números reais. 2. As questões envolvem cálculos, simplificações, equivalências e propriedades de expressões algébricas e operações com prefixos do Sistema Internacional de Unidades. 3. Há um gabarito no final com as respostas corretas para cada uma das 17 questões.

1. LISTAS DE EXERCÍCIOS
EXPRESSÕES

2. EXPRESSÕES
1
01. (Famerp 2018) Um granjeiro tem estoque de ração para alimentar 420 galinhas por 80 dias. Depois de x dias de
uso desse estoque, o granjeiro vendeu 70 das 420 galinhas. Com a venda, o restante do estoque de ração durou 12
dias a mais do que esse restante de ração duraria se ele não tivesse vendido as galinhas. Supondo que o consumo
diário de ração de cada galinha seja sempre o mesmo, x é igual a
a) 20.
b) 16.
c) 18.
d) 22.
e) 24.
02. (Mackenzie 2018) Se x e y são números reais não nulos tais que
x
xy x y,
y
= = − então o valor de x y
+ é igual a
a)
3
2
−
b)
1
2
−
c) 0
d)
1
2
e)
3
2
03. (Ifsp 2017) Com relação à potenciação e radiciação, analise as assertivas abaixo.
I. O resultado da expressão 3
5 3 36 : 16 7
× + − igual a 137.
II. O resultado da expressão 4
16 2 : 4 225 27
− + × está entre 420 e 440.
III. A raiz quadrada de oitenta e um é igual a três elevado ao quadrado.
É correto o que se afirma em
a) III, apenas
b) I, apenas
c) I e III, apenas
d) II, apenas
e) I, II e III

3. EXPRESSÕES
2
04. (Fac. Albert Einstein 2016) A tabela seguinte permite exprimir os valores de certas grandezas em relação a um
valor determinado da mesma grandeza tomado como referência. Os múltiplos e submúltiplos decimais das unidades
do Sistema Internacional de Unidades (SI) podem ser obtidos direta ou indiretamente dos valores apresentados e têm
seus nomes formados pelo emprego dos prefixos indicados.
NOME SÌMBOLO FATOR PELO QUAL A UNIDADE É MULTIPLICADA
tera T
12
10 1000 000 000 000
=
giga G 9
10 1000 000 000
=
mega M
6
10 1000 000
=
quilo K
3
10 1000
=
hecto h 2
10 100
=
deca da 10 10
=
deci d 1
10 0,1
−
=
centi c 2
10 0,01
−
=
mili m 3
10 0,001
−
=
micro μ 6
10 0,000 001
−
=
nano n
9
10 0,000 000 001
−
=
pico p 12
10 0,000 000 000 001
−
=
Por exemplo, se a unidade de referência fosse o ampère (A), teríamos:
3
6
6
152 10
152 000 A 152 000 10 A A 0,152 A
10
μ − ⋅
= ⋅ = =
Se o grama (g) for a unidade de referência e
9
(12 500 10 Gg) (0,0006 ng)
X ,
0,000 012 Tg
⋅ ⋅
= então o valor de X, em gramas, é tal
que
a) X 500
<
b) 500 X 1000
< <
c) 1000 X 1500
< <
d) X 1500
>

4. EXPRESSÕES
3
05. (Fuvest 2016) De 1869 até hoje, ocorreram as seguintes mudanças de moeda no Brasil: (1) em 1942, foi criado o
cruzeiro, cada cruzeiro valendo mil réis; (2) em 1967, foi criado o cruzeiro novo, cada cruzeiro novo valendo mil
cruzeiros; em 1970, o cruzeiro novo voltou a se chamar apenas cruzeiro; (3) em 1986, foi criado o cruzado, cada
cruzado valendo mil cruzeiros; (4) em 1989, foi criado o cruzado novo, cada um valendo mil cruzados; em 1990, o
cruzado novo passou a se chamar novamente cruzeiro; (5) em 1993, foi criado o cruzeiro real, cada um valendo mil
cruzeiros; (6) em 1994, foi criado o real, cada um valendo 2.750 cruzeiros reais. Quando morreu, em 1869, Brás Cubas
possuía 300 contos. Se esse valor tivesse ficado até hoje em uma conta bancária, sem receber juros e sem pagar taxas,
e se, a cada mudança de moeda, o depósito tivesse sido normalmente convertido para a nova moeda, o saldo
hipotético dessa conta seria, aproximadamente, de um décimo de
Dados:
Um conto equivalia a um milhão de réis.
Um bilhão é igual a 9
10 e um trilhão é igual a 12
10 .
a) real.
b) milésimo de real.
c) milionésimo de real.
d) bilionésimo de real.
e) trilionésimo de real.
06. (Insper 2016) Se 2 2 2
x y z xy xz yz 6,
+ + = + + = então um possível valor para a soma x y z
+ + é
a) 6.
b) 2 2.
c) 2 3.
d) 3 2.
e) 3 3.
07. (Fac. Albert Einstein 2016) Dispõe-se de 900 frascos de um mesmo tipo de medicamento e pretende-se dividi-los
igualmente entre X setores de certo hospital. Sabendo que, se tais frascos fossem igualmente divididos entre 3
setores a menos, cada setor receberia 15 frascos a mais do que o previsto inicialmente, então X é um número
a) menor do que 20
b) maior do que 50
c) quadrado perfeito
d) primo
08. (Fac. Albert Einstein - 2016) Certo dia, a administração de um hospital designou duas de suas enfermeiras -
Antonieta e Bernardete - para atender os 18 pacientes de um ambulatório. Para executar tal incumbência, elas
dividiram o total de pacientes entre si, em quantidades que eram, ao mesmo tempo, inversamente proporcionais às
suas respectivas idades e diretamente proporcionais aos seus respectivos tempos de serviço no hospital. Sabendo que
Antonieta tem 40 anos de idade e trabalha no hospital há 12 anos, enquanto que Bernardete tem 25 anos e lá trabalha
há 6 anos, é correto afirmar que
a) Bernardete atendeu 10 pacientes.
b) Antonieta atendeu 12 pacientes.
c) Bernardete atendeu 2 pacientes a mais do que Antonieta.
d) Antonieta atendeu 2 pacientes a mais do que Bernardete.

5. EXPRESSÕES
4
09. (Fuvest 2016) A igualdade correta para quaisquer a e b, números reais maiores do que zero, é
a) 3 3 3
a b a b
+ = +
b)
2 2
1 1
b
a a b
= −
− +
c) 2
( a b) a b
− =
−
d)
1 1 1
a b a b
= +
+
e)
3 3
2 2
a b
a b
a ab b
−
= −
+ +
10. (Insper 2015) Considere dois números positivos x e y, com x y,
> tais que
2 2
x y x y 8
.
x y 15
 + + − =


 − =

Nessas condições, 2x é igual a
a) 31.
b) 32.
c) 33.
d) 34.
e) 35.
11. (Insper 2014) Sendo x e y dois números reais não nulos, a expressão 2 2 1
(x y )
− − −
+ é equivalente a
a)
2 2
2 2
x y
.
x y
+
b)
2
xy
.
x y
 
 
+
 
c)
2 2
x y
.
2
+
d) ( )2
x y .
+
e) 2 2
x y .
+
12. (Ifsp 2014) O valor da expressão
2 3
2
2 2
2
− −
−
é igual a
a)
5
4
1 2
.
2
−
b) 3
2 .
−
c) 5
2 .
−
−
d) 5
2 .
−
e)
5
4
2 1
.
2
−

6. EXPRESSÕES
5
13. (Insper 2009) O valor de
2
2
2009 4
2009 2009 2
−
+ −
é igual a
a)
2007
2008
b)
2008
2009
c)
2007
2009
d)
2009
2008
e)
2009
2007
14. (Unifesp 2008) Se 0 < a < b, racionalizando o denominador, tem-se que
1 b a
.
b a
a b
−
=
−
+
Assim o valor da soma
1 1 1 1
...
1 2 2 3 3 4 999 1000
+ + + +
+ + + +
é
a) 10 10 1.
−
b) 10 10.
c) 99.
d) 100.
e) 101.
15. (Fatec 2008) Seja k um número real positivo. Simplificando a expressão ( ) ( )
2
0,5 0,5 1
k k 3 k
− −
+ − + obtém-se
a) k.
b) k 1.
−
c) k 3.
−
d) 1
k k .
−
−
e) 1
k 2k 3.
−
+ −
16. (Fatec 2003) O valor da expressão y =
3
2
x 8
x 2x 4
−
+ +
, para x = 2 , é
a) 2 - 2
b) 2 + 2
c) 2
d) - 0,75
e) - 4
3
17. (Mackenzie 2001) Se k é um número real maior que zero, então
2
1
k 1 k
+ −
a) diminui quando k aumenta.
b) é menor que 0.
c) está entre 0 e k.
d) está entre k e 2k.
e) é maior que 2k.

7. EXPRESSÕES
6
GABARITO
1 - A 2 - A 3 - C 4 - B 5 - D
6 - D 7 - A 8 - D 9 - E 10 - D
11 - A 12 -D 13 - A 14 - A 15 - B
16 - A 17 - E