Exercicios de geometria_reg_4etapa

Interbits – SuperPro ® Web
EXERCÍCIOS DE GEOMETRIA
1. Uma construtora, para construir o novo prédio da biblioteca de uma universidade, cobra um
valor fixo para iniciar as obras e mais um valor, que aumenta de acordo com o passar dos
meses da obra. O gráfico abaixo descreve o custo da obra, em milhões de reais, em função do
número de meses utilizados para a construção da obra.
a) Obtenha a lei y = f ( x) , para x ³ 0, que determina o gráfico.
b) Determine o valor inicial cobrado pela construtora para a construção do prédio da biblioteca.
c) Qual será o custo total da obra, sabendo que a construção demorou 10 meses para ser
finalizada?
Resposta:
a) Como o gráfico de f é uma reta, segue que f(x) = ax + b. Logo, sabendo que b é a
ordenada do ponto de interseção do gráfico de f com o eixo y, temos que b = 2. Além
disso, como o gráfico passa pelo ponto (12, 8), segue que a taxa de variação de f é tal que
8 a 12 2 a 1.
2
= ´ + Û =
Portanto, f(x) 1 x 2,
= + com x ³ 0.
2
b) De (a), temos que o valor inicial, cobrado pela construtora para a construção do prédio da
biblioteca, é igual a 2 milhões.
c) Se a construção demorou 10 meses para ser finalizada, então o custo total da obra foi de
f(10) 1 10 2 7
= ´ + = milhões de reais.
2
2. Os gráficos abaixo representam as funções receita mensal R(x) e custo mensal C(x) de
um produto fabricado por uma empresa, em que x é a quantidade produzida e vendida. Qual o
lucro obtido ao se produzir e vender 1350 unidades por mês?
Página 1 de 24

a) 1740
b) 1750
c) 1760
d) 1770
e) 1780
Resposta:
[B]
C( x) = 15000 - 5000 Custo: ´ x + 5000 = 10x +
5000
1000
15000 - 0 Receita: R( x) = ´ x =
15x
1000
Lucro:
( ) ( ) ( )
( ) ( )
( )
( ) ( )
( )
L x R x – C x
L x 15x – 10x 5000
L x 5x – 5000
L 1350 5. 1350 – 5000
L 1350 1750
==
+
=
==
3. Uma pesquisa mostra como a transformação demográfica do país, com o aumento da
expectativa de vida, vai aumentar o gasto público na área social em centenas de bilhões de
reais. Considere que os gráficos dos aumentos com aposentadoria e pensões, educação e
saúde sejam, aproximadamente, linhas retas de 2010 a 2050.
a) Faça uma estimativa de qual será o gasto com aposentadorias e pensões em 2050.
b) Calcule o gasto público com educação em 2050.
Página 2 de 24

c) Considerando que os gráficos dos aumentos com aposentadoria e pensões, educação e
saúde continuem crescendo mediante linhas retas, existirá algum momento, depois de 2010,
em que os gráficos se interceptarão?
Resposta:
Aumento anual do item Aposentadoria e pensões:
5,6 - 2,2 =
0,17.
30 -
10
Aumento anual do item Educação:
4 - 2 =
0,1.
30 -
10
Aumento anual Saúde:
3,6 - 1,8 =
0,09.
30 -
10
a) Aposentadorias e pensões em 2050: 5,6 + 20 ´0,17 = 9 centenas de bilhões de reais.
b) Gastos com educação em 2050: 4 + 0,1 ´20 = 6 centenas de bilhões de reais.
c) Não se interceptarão, pois 0,17 > 0,1 > 0,09.
4. Conforme divulgado pela ONU (Organização das Nações Unidas), a população mundial
atingiu, em outubro ultimo, 7 bilhões de pessoas.
Suponha que o modelo matemático que permita obter uma estimativa dessa população, no
mês de outubro, daqui a t anos, seja a equação da reta do gráfico abaixo. Assinale a alternativa
em que constam, respectivamente, essa equação e o ano em que, de acordo com ela, a
população mundial atingiria 10 bilhões de seres humanos.
EQUAÇÃO ANO
a)
p 1 t 7
= + 2050
8
b) p 1 t 8
= + 2039
7
c)
p 1 t 7
= + 2050
13
d)
p 1 t 7
= + 2100
13
e)
p 1 t 7
= + 2013
8
Resposta:
Página 3 de 24

[C]
Seja p(t) = at + b a lei da função p.
Como p(0) = 7, segue que b = 7. Além disso, temos que a taxa de variação da função p é
8 - 7 1 dada por
a = =
.
13 -
0 13
Desse modo, a população mundial será igual a 10 bilhões quando p(t) = 10, ou seja,
10 = 1 t + 7 Û t =
39.
13
Supondo que “outubro último” corresponda a outubro de 2011, segue que a população mundial
atingirá 10 bilhões em 2011+ 39 = 2050.
5. Qual dos gráficos abaixo representa a reta de equação y = 2x + 3?
a)
b)
c)
d)
Página 4 de 24

e)
Resposta:
[A]
x = 0Þ y = 3 e y = 0 Þ x = -1,5
Considerando os pontos (0,3) e (-1,5; 0), temos o gráfico:
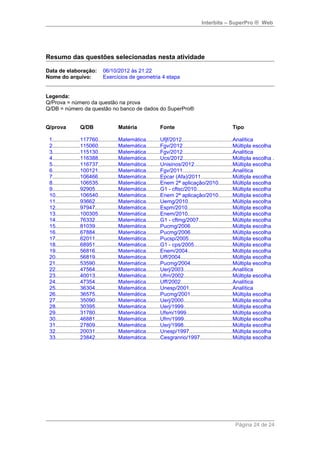
6. Nos últimos anos, o salário mínimo tem crescido mais rapidamente que o valor da cesta
básica, contribuindo para o aumento do poder aquisitivo da população. O gráfico abaixo ilustra
o crescimento do salário mínimo e do valor da cesta básica na região Nordeste, a partir de
2005.
Suponha que, a partir de 2005, as evoluções anuais dos valores do salário mínimo e dos
preços da cesta básica, na região Nordeste, possam ser aproximados mediante funções
polinomiais do 1º grau, f (x) = ax + b, em que x representa o número de anos transcorridos
após 2005.
a) Determine as funções que expressam os crescimentos anuais dos valores do salário mínimo
e dos preços da cesta básica, na região Nordeste.
b) Em que ano, aproximadamente, um salário mínimo poderá adquirir cerca de três cestas
básicas, na região Nordeste? Dê a resposta aproximando o número de anos, após 2005, ao
inteiro mais próximo.
Página 5 de 24

Resposta:
a) Seja S: ¡ ® ¡ , definida por S(x) = ax + b, com S(x) sendo o salário mínimo x anos após
2005. Logo,
a = 510 - 300 =
42
5 -
0
e b = S(0) = 300.
Portanto,
S(x) = 42x + 300.
Seja C: ¡ ® ¡ , definida por C(x) = a' x + b', com C(x) sendo o valor da cesta básica x
anos após 2005. Assim,
a' = 184 - 154 =
6
5 -
0
e b' = C(0) = 154.
Por conseguinte,
C(x) = 6x +154.
b) Queremos calcular o menor inteiro x para o qual S(x) ³ 3 ´C(x).
42x + 300 ³ 3 ´(6x +154)Þ8x ³ 54Þ x ³ 6,75.
Portanto, o menor inteiro x para o qual S(x) ³ 3 ´C(x) é 7 e, assim, em 2012 um salário
mínimo poderá adquirir três cestas básicas.
7. Luiza possui uma pequena confecção artesanal de bolsas. No gráfico abaixo, a reta c
representa o custo total mensal com a confecção de x bolsas e a reta f representa o
faturamento mensal de Luiza com a confecção de x bolsas.
Com base nos dados acima, é correto afirmar que Luiza obtém lucro se, e somente se, vender
Página 6 de 24

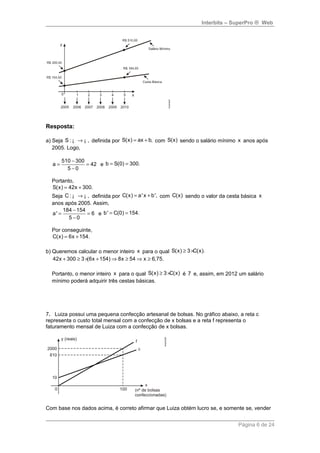
a) no mínimo 2 bolsas.
b) pelo menos 1 bolsa.
c) exatamente 3 bolsas.
d) no mínimo 4 bolsas.
Resposta:
[B]
c(x) = 10 + 8x e f(x) = 20x.
Fazendo f(x) > c(x), temos:
20x > 10 + 8x
12x > 10
x > 10/12
Logo, deverá ser vendida pelo menos uma bolsa.
8. Uma torneira gotejando diariamente é responsável por grandes desperdícios de água.
Observe o gráfico que indica o desperdício de uma torneira:
Se y representa o desperdício de água, em litros, e x representa o tempo, em dias, a relação
entre x e y é
a) y = 2 x
b)
y 1 x
2
=
c) y = 60 x
d) y = 60 x +1
e) y = 80 x + 50
Resposta:
[C]
Seja f : ¡ ®¡ a função linear definida por f(x) = ax, em que f(x) representa o desperdício de
água, em litros, após x dias.
a 600 0 60.
A taxa de variação da função f é dada por = - =
10 -
0
Página 7 de 24

Portanto, segue que f(x) = y = 60x.
9. O volume de água de um reservatório aumenta em função do tempo, de acordo com o
gráfico abaixo:
Para encher este reservatório de água com 2500 litros, uma torneira é aberta. Qual o tempo
necessário para que o reservatório fique completamente cheio?
a) 7h
b) 6h50min
c) 6h30min
d) 7h30min
e) 7h50min
Resposta:
[D]
Temos o gráfico de uma função linear do tipo V = k.t
Fazendo t = 3 temos V = 1
1= k.3 Û k =
1
3
logo
V 1.k
3
=
Se V = 2500 L = 2,5 m3 temos:
2,5 =
1.t t 7,5h
3
Û = , ou seja, 7 horas e 30 minutos.
10. As sacolas plásticas sujam florestas, rios e oceanos e quase sempre acabam matando por
asfixia peixes, baleias e outros animais aquáticos. No Brasil, em 2007, foram consumidas 18
bilhões de sacolas plásticas. Os supermercados brasileiros se preparam para acabar com as
sacolas plásticas até 2016. Observe o gráfico a seguir, em que se considera a origem como o
ano de 2007.
Página 8 de 24

De acordo com as informações, quantos bilhões de sacolas plásticas serão consumidos em
2011?
a) 4,0
b) 6,5
c) 7,0
d) 8,0
e) 10,0
Resposta:
[E]
Seja a função N: ¡ ® ¡ , definida por N(n) = an + b, em que N(n) é o número de sacolas
consumidas, em bilhões, n anos após 2007.
Do gráfico, temos que o valor inicial de N é b = 18.
a 0 18 2.
A taxa de variação da função N é dada por = - = -
9 -
0
Desse modo, segue que N(n) = -2n +18. Queremos calcular o número de sacolas consumidas
em 2011, ou seja, N(4).
Portanto,N(4) = -2´4 +18 = 10.
11. “Em janeiro de 2008, o Brasil tinha 14 milhões de usuários residenciais na rede
mundial de computadores. Em fevereiro de 2008, esses internautas somavam 22 milhões de
pessoas - 8 milhões, ou 57% a mais. Deste total de usuários, 42% ainda não usam banda larga
(internet mais rápida e estável). Só são atendidos pela rede discada”.
Atualidade e Vestibular 2009, 1º semestre, ed Abril
Baseando-se nessa informação, observe o gráfico, a seguir:
Página 9 de 24

Se mantida, pelos próximos meses, a tendência de crescimento linear, mostrada no gráfico
acima, o número de usuários residenciais de computadores, em dezembro de 2009, será igual
a
a) 178 x 106.
b) 174 x 105.
c) 182 x 107.
d) 198 x 106.
Resposta:
[D]
Número de usuários em dezembro de 2009 será 14 milhões(dezembro de 2008) + 23. 8
milhões, ou seja 198 milhões.
Resposta 198.106 habitantes.
12. O gráfico abaixo mostra o número de pessoas comprovadamente infectadas pelo vírus
H1N1 numa certa cidade do Brasil, entre os meses de maio e setembro de 2009. Na hipótese
de um crescimento linear desse surto, representado pela reta r, pode-se prever que o número
de pessoas infectadas em dezembro de 2009 será igual a:
a) 30
b) 36
c) 40
d) 44
e) 48
Página 10 de 24

Resposta:
[B]
Maio: x = 5 e y = 8
Junho: x = 6 e y = 12
Como a função é linear, temos: y = ax + b
a = 12 -
8 =
4
6 -
5
Y = 4x + b
12 = 4.6 + b
b = -12
Logo, y = 4x – 12
No mês de dezembro, temos:
y = 4.12 – 12 = 36
13. O gráfico mostra o número de favelas no município do Rio de Janeiro entre 1980 e 2004,
considerando que a variação nesse número entre os anos considerados é linear.
Se o padrão na variação do período 2004/2010 se mantiver nos próximos 6 anos, e sabendo
que o número de favelas em 2010 e 968, então o número de favelas em 2016 será
a) menor que 1150.
b) 218 unidades maior que em 2004.
c) maior que 1150 e menor que 1200.
d) 177 unidades maior que em 2010.
e) maior que 1200.
Resposta:
[C]
Variação entre 2004 e 2010 = 968 – 750 = 218
Logo, em 2016 teremos: 968 + 218 = 1186 favelas.
Página 11 de 24

14. Uma empresa de táxi E1 cobra R$ 2,00 a "bandeirada", que é o valor inicial da corrida, e
R$ 2,00 por km rodado. Outra empresa E2 fixa em R$ 3,00 o km rodado e não cobra a
bandeirada. As duas tarifas estão melhor representadas, graficamente, em
Resposta:
[B]
15. Acompanhando o desenvolvimento de uma população de vírus, certo biólogo montou a
seguinte tabela, que apresenta o número de vírus ao final de cada um dos 5 primeiros minutos:
Supondo-se que o ritmo de crescimento dessa população tenha continuado a obedecer a essa
mesma lei, o número de vírus, ao final de 50 minutos, era:
a) 87
b) 90
c) 197
d) 200
Resposta:
[C]
Página 12 de 24

16. O gráfico representa a variação da temperatura T, medida em graus Celsius, de uma barra
de ferro em função do tempo t, medido em minutos.
Com base nas informações do gráfico, pode-se estimar que a temperatura dessa barra atingiu
0°C no instante t igual a:
a) 1 min 15 s
b) 1 min 20 s
c) 1 min 25 s
d) 1 min 30 s
Resposta:
[A]
17. Um grupo de amigos "criou" uma nova unidade de medida para temperaturas: o grau
Patota. Estabeleceram, então, uma correspondência entre as medidas de temperaturas em
graus Celsius (°C), já conhecida, e em graus Patota (°P), mostrada na tabela a seguir.
Lembrando que a água ferve a 100°C, então, na unidade Patota ela ferverá a
a) 96°
b) 88°
c) 78°
d) 64°
e) 56°
Página 13 de 24

Resposta:
[E]
18. Todos os anos, no mundo, milhões de bebês morrem de causas diversas. É um número
escandaloso, mas que vem caindo. O caminho para se atingir o objetivo dependerá de muitos e
variados meios, recursos, políticas e programas - dirigidos não só às crianças mas às suas
famílias e comunidades.
Admitindo-se que os pontos do gráfico acima pertencem a uma reta, a mortalidade infantil em
2015, em milhões, será igual a
a) 9
b) 8
c) 7
d) 6
e) 5
Resposta:
[B]
19.
Na seleção para as vagas deste anúncio, feita por telefone ou correio eletrônico, propunha-se
aos candidatos uma questão a ser resolvida na hora. Deveriam calcular seu salário no primeiro
mês, se vendessem 500 m de tecido com largura de 1,40 m, e no segundo mês, se
vendessem o dobro. Foram bem sucedidos os jovens que responderam, respectivamente,
a) R$ 300,00 e R$ 500,00.
Página 14 de 24

b) R$ 550,00 e R$ 850,00.
c) R$ 650,00 e R$ 1000,00.
d) R$ 650,00 e R$ 1300,00.
e) R$ 950,00 e R$ 1900,00.
Resposta:
[C]
O salário no primeiro mês é dado por
300 + 0,5 ´500 ´1,4 = R$ 650,00.
No segundo mês, vendendo o dobro de metros quadrados de tecido, o salário será de
300 + 2 ´0,5 ´500 ´1,4 = R$ 1.000,00.
20. Um grande poluente produzido pela queima de combustíveis fósseis é o SO2 (dióxido de
enxofre).
Uma pesquisa realizada na Noruega e publicada na revista "Science" em 1972 concluiu que o
número (N) de mortes por semana, causadas pela inalação de SO2, estava relacionado com a
concentração média (C), em mg/m3, do SO2 conforme o gráfico a seguir: os pontos (C, N)
dessa relação estão sobre o segmento de reta da figura.
Com base nos dados apresentados, a relação entre N e C (100 ≤ C ≤ 700) pode ser dada por:
a) N = 100 - 700 C
b) N = 94 + 0,03 C
c) N = 97 + 0,03 C
d) N = 115 - 94 C
e) N = 97 + 600 C
Resposta:
[B]
Página 15 de 24

21. A tabela mostra a expectativa de vida ao nascer de pessoas de um certo país:
Supondo-se que a expectativa de vida aumente de forma linear, pode-se afirmar que uma
pessoa nascida nesse país, no ano de 2010, deverá viver:
Considere 1 ano como tendo 365 dias.
a) 77 anos e 6 meses.
b) 79 anos e 8 meses.
c) 77 anos, 7 meses e 9 dias.
d) 79 anos, 9 meses e 21 dias.
Resposta:
[C]
22. O gráfico adiante representa, em bilhões de dólares, a queda das reservas internacionais
de um determinado país no período de julho de 2000 a abril de 2002.
Admita que, nos dois intervalos do período considerado, a queda de reservas tenha sido linear.
Determine o total de reservas desse país, em bilhões de dólares, em maio de 2001.
Resposta:
Página 16 de 24

total de reservas = 24,26 bilhões de dólares
23. Um comerciante decidiu fabricar camisetas de malha para vendê-las na praia, ao preço de
R$ 8,00 a unidade. Investiu no negócio R$ 320,00. Sabendo que o lucro(y) obtido é função da
quantidade de unidades vendidas(x), o gráfico que mais se aproxima da representação dessa
função é:
Resposta:
[B]
24. A Cerâmica Marajó concede uma gratificação mensal a seus funcionários em função da
produtividade de cada um convertida em pontos; a relação entre a gratificação e o número de
pontos está representada no gráfico a seguir.
Observando que, entre 30 e 90 pontos, a variação da gratificação é proporcional à variação do
número de pontos, determine a gratificação que um funcionário receberá no mês em que
obtiver 100 pontos.
Página 17 de 24

Resposta:
R$ 710,00.
25. Apresentamos a seguir o gráfico do volume do álcool em função de sua massa, a uma
temperatura fixa de 0°C.
Baseado nos dados do gráfico, determine:
a) a lei da função apresentada no gráfico;
b) qual é a massa (em gramas) de 30 cm3 de álcool.
Resposta:
a) v = 5
4
m, com m ≥ 0
b) 24 g
26. O gráfico da função f(x) = ax + b está representado na figura.
Página 18 de 24

O valor de a + b é:
a) -1
b) 2
5
c)
3
2
d) 2
Resposta:
[C]
27. Observe o gráfico a seguir:
Crepúsculo da garrafa azul
Os brasileiros estão trocando o vinho branco alemão por produto de melhor qualidade (em
milhões de litros).
("Veja", 10./09/1999)
Se o consumo de vinho branco alemão, entre 1994 e 1998, sofreu um decréscimo linear, o
volume total desse consumo em 1995, em milhões de litros, corresponde a:
a) 6,585
b) 6,955
Página 19 de 24

c) 7,575
d) 7,875
Resposta:
[D]
28. Em uma partida, Vasco e Flamengo levaram ao Maracanã 90.000 torcedores. Três
portões foram abertos às 12 horas e até as 15 horas entrou um número constante de pessoas
por minuto. A partir desse horário, abriram-se mais 3 portões e o fluxo constante de pessoas
aumentou.
Os pontos que definem o número de pessoas dentro do estádio em função do horário de
entrada estão contidos no gráfico a seguir:
Quando o número de torcedores atingiu 45.000, o relógio estava marcando 15 horas e:
a) 20 min
b) 30 min
c) 40 min
d) 50 min
Resposta:
[B]
29. A figura representa o gráfico de uma função do 10. Grau que passa pelos pontos A e B,
onde a ≠ 2.
Página 20 de 24

O ponto de interseção da reta AB com eixo x tem abscissa igual a
a) 1 - a
b) a - 2
c)
( 3a -
12
)
( a -
2
)
d) 4 - a
e) 12 - 3a
Resposta:
[D]
30. Na figura a seguir, tem-se o gráfico de uma reta que representa a quantidade, medida em
mL, de um medicamento que uma pessoa deve tomar em função de seu peso, dado em kgf,
para tratamento de determinada infecção.
O medicamento deverá ser aplicado em seis doses.
Assim, uma pessoa que pesa 85kgf receberá em cada dose:
a) 7 mL
b) 9 mL
c) 8 mL
d) 10 mL
Resposta:
Página 21 de 24

[B]
31. A promoção de uma mercadoria em um supermercado está representada, no gráfico a
seguir, por 6 pontos de uma mesma reta.
Quem comprar 20 unidades dessa mercadoria, na promoção, pagará por unidade, em reais, o
equivalente a:
a) 4,50
b) 5,00
c) 5,50
d) 6,00
Resposta:
[A]
32. O gráfico mostra o resultado de uma experiência relativa à absorção de potássio pelo
tecido da folha de um certo vegetal, em função do tempo e em condições diferentes de
luminosidade.
Nos dois casos, a função linear y = mx ajustou-se razoavelmente bem aos dados, daí a
referência a "m" como taxa de absorção (geralmente medida em ì moles por unidade de peso
Página 22 de 24

por hora). Com base no gráfico, se m1 é a taxa de absorção no claro e m2 a taxa de absorção
no escuro, a relação entre essas duas taxas é:
a) m1 = m2.
b) m2 = 2m1.
c) m1 . m2 = 1.
d) m1 . m2 = -1.
e) m1 = 2m2.
Resposta:
[E]
33. Uma barra de ferro com temperatura inicial de -10°C foi aquecida até 30°C. O gráfico
anterior representa a variação da temperatura da barra em função do tempo gasto nessa
experiência. Calcule em quanto tempo, após o início da experiência, a temperatura da barra
atingiu 0°C.
a) 1 min
b) 1 min 5 seg
c) 1 min e 10 seg
d) 1 min e 15 seg
e) 1 min e 20 seg
Resposta:
[D]
Página 23 de 24

Resumo das questões selecionadas nesta atividade
Data de elaboração: 06/10/2012 às 21:22
Nome do arquivo: Exercícios de geometria 4 etapa
Legenda:
Q/Prova = número da questão na prova
Q/DB = número da questão no banco de dados do SuperPro®
Q/prova Q/DB Matéria Fonte Tipo
1..................117760.............Matemática.........Ufjf/2012.................................Analítica
2..................115060.............Matemática.........Fgv/2012.................................Múltipla escolha
3..................115130.............Matemática.........Fgv/2012.................................Analítica
4..................116388.............Matemática.........Ucs/2012.................................Múltipla escolha .
5..................116737.............Matemática.........Unisinos/2012.........................Múltipla escolha
6..................100121.............Matemática.........Fgv/2011.................................Analítica
7..................106466.............Matemática.........Epcar (Afa)/2011.....................Múltipla escolha
8..................106535.............Matemática.........Enem 2ª aplicação/2010.........Múltipla escolha
9..................92905...............Matemática.........G1 - cftsc/2010.......................Múltipla escolha
10................106540.............Matemática.........Enem 2ª aplicação/2010.........Múltipla escolha
11................93662...............Matemática.........Uemg/2010.............................Múltipla escolha
12................97947...............Matemática.........Espm/2010..............................Múltipla escolha
13................100305.............Matemática.........Enem/2010.............................Múltipla escolha
14................76332...............Matemática.........G1 - cftmg/2007......................Múltipla escolha
15................81039...............Matemática.........Pucmg/2006............................Múltipla escolha
17................62011...............Matemática.........Pucsp/2005.............................Múltipla escolha
18................68951...............Matemática.........G1 - cps/2005.........................Múltipla escolha
19................56816...............Matemática.........Enem/2004.............................Múltipla escolha
20................56819...............Matemática.........Uff/2004..................................Múltipla escolha
22................47564...............Matemática.........Uerj/2003................................Analítica
23................40013...............Matemática.........Ufrn/2002................................Múltipla escolha
24................47354...............Matemática.........Uff/2002..................................Analítica
25................36304...............Matemática.........Unesp/2001............................Analítica
27................35090...............Matemática.........Uerj/2000................................Múltipla escolha
29................31780...............Matemática.........Ufsm/1999..............................Múltipla escolha
30................46881...............Matemática.........Ufrn/1999................................Múltipla escolha
32................20031...............Matemática.........Unesp/1997............................Múltipla escolha
33................23842...............Matemática.........Cesgranrio/1997.....................Múltipla escolha
Página 24 de 24

Exercicios de geometria_reg_4etapa

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Exercicios de geometria_reg_4etapa

Exercicios de geometria_reg_4etapa