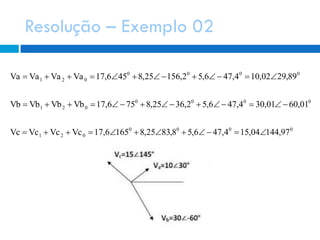
1) As componentes simétricas são ferramentas para analisar circuitos polifásicos desequilibrados, decompondo-os em sistemas equilibrados.
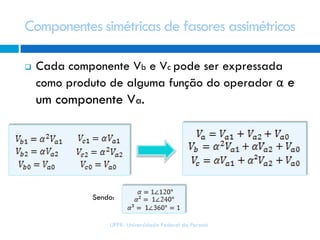
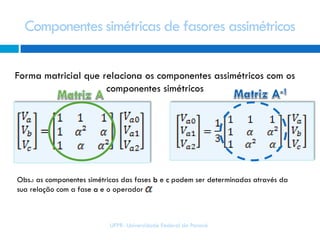
2) Elas simplificam cálculos de falta, representando condições assimétricas usando cálculo monofásico.
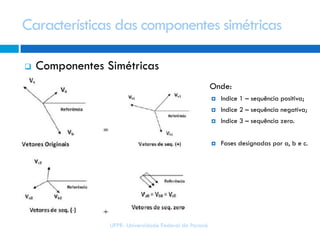
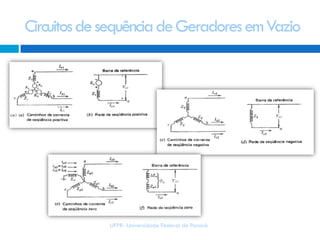
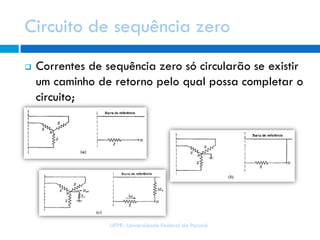
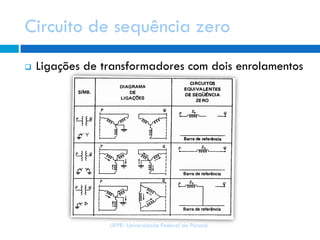
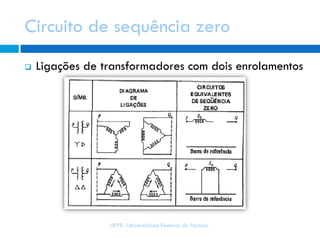
3) Existem componentes de sequência positiva, negativa e zero, associadas a sistemas trifásicos equilibrados ou envolvendo a terra.