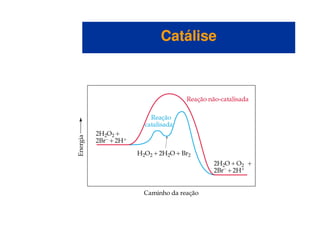
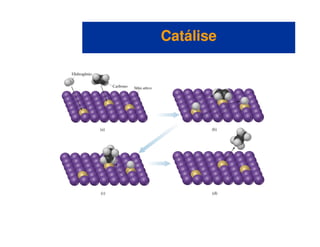
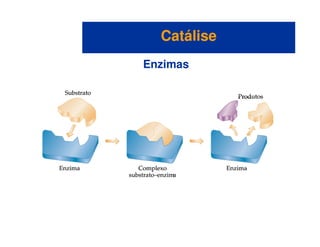
O documento discute os conceitos fundamentais de cinética química. A cinética química estuda a velocidade das reações químicas e como fatores como concentração, temperatura e catalisadores afetam essa velocidade. Existem diferentes maneiras de medir a velocidade de reação e ela depende da ordem da reação. O modelo de colisão explica como a velocidade aumenta com a concentração e temperatura à medida que mais moléculas colidem com a orientação correta e energia necessária para reagir.




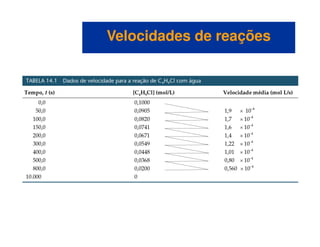
![Variação da concentração com o tempo
– Podemos calcular a velocidade média em termos do
desaparecimento do C4H9Cl.
– A unidade para a velocidade média é mol/L s.
– A velocidade média diminui com o tempo.
Velocidades de reaçõesVelocidades de reações
– A velocidade média diminui com o tempo.
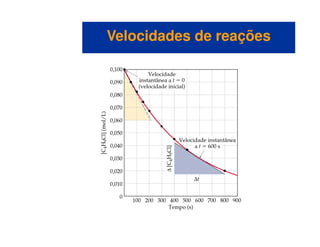
– Representamos graficamente [C4H9Cl] versus tempo.
– A velocidade a qualquer instante de tempo (velocidade
instantânea) é a inclinação da tangente da curva.
– A velocidade instantânea é diferente da velocidade média.
– Geralmente chamamos a velocidade instantânea de velocidade.](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-6-320.jpg)

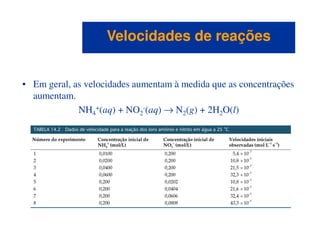
![• Para a reação
NH4
+(aq) + NO2
-(aq) → N2(g) + 2H2O(l)
observamos que
– à medida que a [NH4
+] duplica com a [NO2
-] constante, a
velocidade dobra,
Concentração e velocidadeConcentração e velocidade
velocidade dobra,
– à medida que a [NO2
-] duplica com a [NH4
+] constante, a
velocidade dobra,
– concluímos que a velocidade ∝ [NH4
+][NO2
-].
• A constante k é a constante de velocidade.](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-10-320.jpg)


![Exercício:
A velocidade inicial de uma reação A + B C foi medida para várias
concentrações iniciais diferentes de A e B, e os resultados são como
seguem:
Número do
Experimento
[A] (mol/L) [B] (mol/L) Veloc. inicial
(mol L-1 s-1)
1 0,100 0,100 4,0 x 10-5
2 0,100 0,200 4,0 x 10-52 0,100 0,200 4,0 x 10-5
3 0,200 0,100 16,0 x 10-5
Usando esses dados, determine (a) a lei de velocidade para a reação; (b)
a magnitude da constante de reação; (c)a velocidade de reação quando
[A] = 0,050 mol/L e [B] = 0,100 mol/L](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-13-320.jpg)
![Pratique:
Os seguintes dados foram medidos para a reação do óxido nítrico com
hidrogênio:
2NO (g) + 2 H2 (g) N2 (g) + 2H2O (g)
Número do
Experimento
[NO] (mol/L) [H2] (mol/L) Veloc. inicial
(mol L-1 s-1)
1 0,10 0,10 1,23 x 10-3
2 0,10 0,20 2,46 x 10-32 0,10 0,20 2,46 x 10-3
3 0,20 0,10 4,92 x 10-3
(a) Determine a lei da velocidade para essa reação.
(b) Calcule a constante de velocidade.
(c) Calcule a velocidade quando [NO] = 0,050 mol/L e [H2] = 0,150
mol/L](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-14-320.jpg)

![Reações de primeira ordem
• Uma representação gráfica de ln[A]t versus t é uma linha reta com
inclinação -k e intercepta em ln[A]0.
• No caso acima utilizamos o logaritmo natural, ln, que é o log na
base e.
Variação da concentraçãoVariação da concentração
com o tempocom o tempo
base e.](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-16-320.jpg)
![Reações de primeira ordem
[ ] [ ]0AlnAln +−= ktt
Variação da concentraçãoVariação da concentração
com o tempocom o tempo](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-17-320.jpg)
![Reações de segunda ordem
• Para uma reação de segunda ordem com apenas um reagente
[ ] [ ]0A
1
A
1
+= kt
t
Variação da concentraçãoVariação da concentração
com o tempocom o tempo
• Um gráfico de 1/[A]t versus t é uma linha reta com inclinação k e
intercepta 1/[A]0
• Para uma reação de segunda ordem, um gráfico de ln[A]t versus t
não é linear.](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-18-320.jpg)
![Reações de segunda ordem
[ ] [ ]0A
1
A
1
+= kt
t
Variação da concentraçãoVariação da concentração
com o tempocom o tempo](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-19-320.jpg)
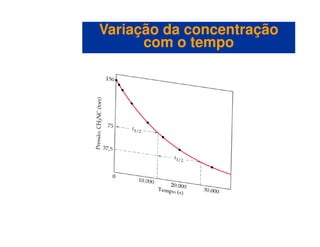
![Meia-vida
• Meia-vida é o tempo que a concentração de um reagente leva para
diminuir para a metade do seu valor inicial.
• Para um processo de primeira ordem, t½ é o tempo gasto para [A]0
alcançar ½[A] .
Variação da concentraçãoVariação da concentração
com o tempocom o tempo
alcançar ½[A]0.
• Matematicamente,
( )
kk
t
693.0ln
2
1
2
1 =−=](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-20-320.jpg)
![Meia-vida
• Para uma reação de segunda ordem, a meia-vida depende da
concentração inicial:
Variação da concentraçãoVariação da concentração
com o tempocom o tempo
concentração inicial:
[ ]0A
1
2
1
k
t −=](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-22-320.jpg)





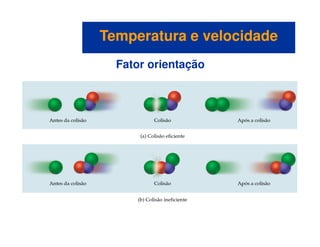


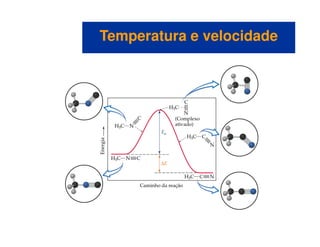


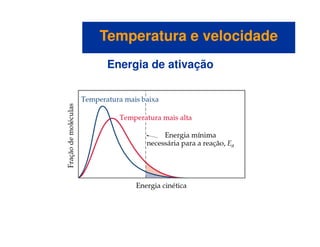


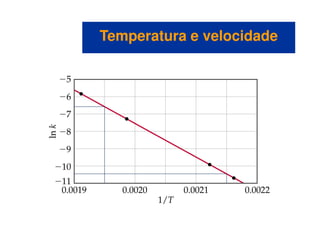






![Mecanismos com uma etapa inicial rápida
2NO(g) + Br2(g) → 2NOBr(g)
• A lei de velocidade determinada experimentalmente é
Velocidade = k[NO]2[Br2]
• Considere o seguinte mecanismo
Mecanismos de reaçãoMecanismos de reação
• Considere o seguinte mecanismo](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-46-320.jpg)
![Mecanismos com uma etapa inicial rápida
• A lei de velocidade é (baseada na Etapa 2):
Velocidade = k2[NOBr2][NO]
• A lei de velocidade não deve depender da concentração de um
intermediário (os intermediários geralmente são instáveis).
• Suponha que NOBr seja instável, então, expressamos a
Mecanismos de reaçãoMecanismos de reação
• Suponha que NOBr2 seja instável, então, expressamos a
concentração de NOBr2 em termos de NOBr e Br2, supondo que
haja um equilíbrio na etapa 1, temos
]NO][Br[]NOBr[ 2
1
1
2
−
=
k
k](https://image.slidesharecdn.com/113373026-cinetica-quimica-130923194629-phpapp01/85/Cinetica-Quimica-47-320.jpg)