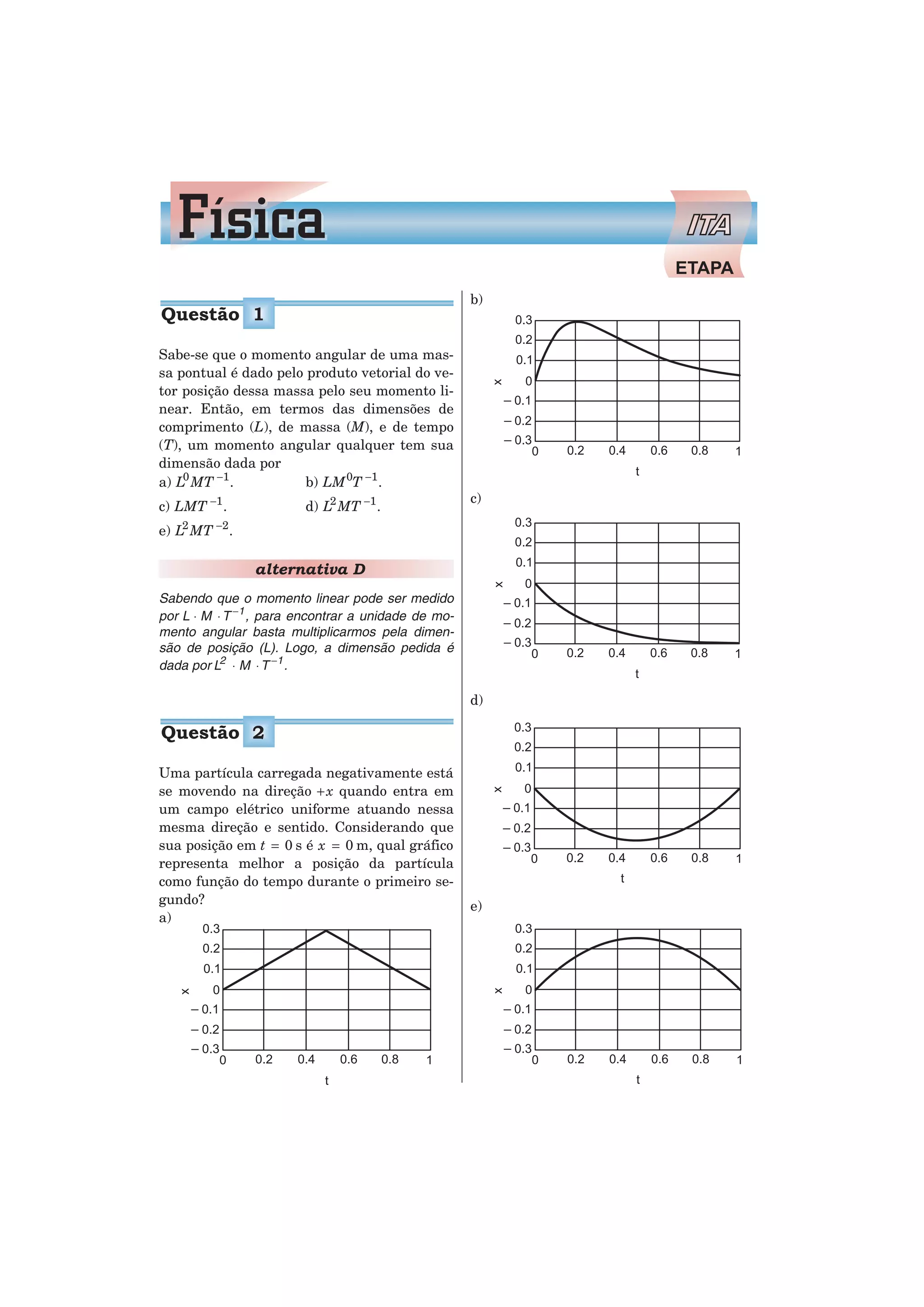
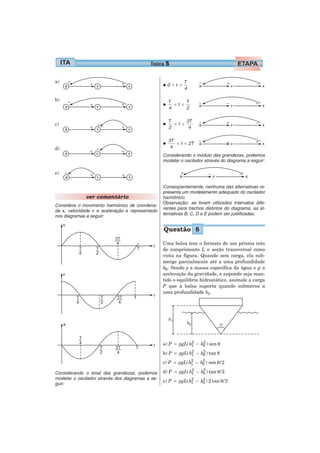
1) Um momento angular tem dimensão L2MT-1. 2) A posição de uma partícula sob ação de um campo elétrico uniforme é representada por uma parábola com concavidade para baixo. 3) O tempo para um barco descer um trecho de rio com os motores desligados é 13h20min.

1. b)
Questão 1
Sabe-se que o momento angular de uma mas-
sa pontual é dado pelo produto vetorial do ve-
tor posição dessa massa pelo seu momento li-
near. Então, em termos das dimensões de
comprimento (L), de massa (M), e de tempo
(T), um momento angular qualquer tem sua
dimensão dada por
a) L0 MT −1 . b) LM 0T −1 .
c)
c) LMT −1 . d) L2 MT −1 .
e) L2 MT −2 .
alternativa D
Sabendo que o momento linear pode ser medido
por L ⋅ M ⋅ T −1 , para encontrar a unidade de mo-
mento angular basta multiplicarmos pela dimen-
são de posição (L). Logo, a dimensão pedida é
dada por L2 ⋅ M ⋅ T −1 .
d)
Questão 2
Uma partícula carregada negativamente está
se movendo na direção + x quando entra em
um campo elétrico uniforme atuando nessa
mesma direção e sentido. Considerando que
sua posição em t = 0 s é x = 0 m, qual gráfico
representa melhor a posição da partícula
como função do tempo durante o primeiro se-
gundo? e)
a)

2. física 3
alternativa E são. No retorno, ao passar em B, verifica ser
de 20,0 km/h sua velocidade escalar média no
Como o campo elétrico é uniforme e atua na mes-
ma direção e sentido da velocidade inicial da partí- percurso então percorrido, ABCB. Finalmen-
cula negativa, a aceleração é constante e tem sen- te, ele chega em A perfazendo todo o percurso
tido oposto ao do campo elétrico, portanto o gráfico de ida e volta em 1,00 h, com velocidade esca-
deve ser uma parábola com a concavidade para lar média de 24,0 km/h. Assinale o módulo v
baixo, o que é representado na alternativa E. do vetor velocidade média referente ao per-
curso ABCB.
Questão 3
Um barco leva 10 horas para subir e 4 horas
para descer um mesmo trecho do rio Amazo-
nas, mantendo constante o módulo de sua ve-
locidade em relação à água. Quanto tempo o
barco leva para descer esse trecho com os mo- a) v = 12,0 km/h b) v = 12,00 km/h
tores desligados? c) v = 20,0 km/h d) v = 20,00 km/h
a) 14 horas e 30 minutos e) v = 36,0 km/h
b) 13 horas e 20 minutos
c) 7 horas e 20 minutos alternativa A
d) 10 horas Admitindo que, perfazendo todo o percurso de ida
e) Não é possível resolver porque não foi dada e volta, a velocidade média seja 24,0 km/h, te-
a distância percorrida pelo barco. mos:
d AB + 3,00 + 3,00 + AB
alternativa B vm = ⇒ 24,0 = ⇒
Δt 1,00
Sendo v B a velocidade do barco em relação à ⇒ AB = 9,00 km
água e v A a velocidade da água em relação à
O intervalo de tempo Δt’ para o ciclista percorrer o
Terra, temos:
trecho ABCB é dado por:
ΔS
vB − v A = AB + 6,00 9,00 + 6,00
10 3 ⋅ ΔS Δt’ = = ⇒ Δt’ = 0,750 h
⇒ vA = v m’ 20,0
ΔS 40
vB + v A = Assim, o módulo v do vetor velocidade média re-
4
ferente ao percurso ABCB é dado por:
Quando o barco descer esse trecho do rio com os
motores desligados, sua velocidade (v B ’) em rela- AB 9,00
v = = ⇒ v = 12,0 km/h
ção à Terra será a própria velocidade da água em Δt’ 0,750
relação à Terra. Assim, temos:
vB ’ = v A
ΔS ΔS 3 ⋅ ΔS 40 Questão 5
vB ’ = ⇒ = ⇒ Δt = h ⇒
Δt Δt 40 3
3 ⋅ ΔS A partir do repouso, um carrinho de monta-
vA =
40 nha russa desliza de uma altura
H = 20 3 m sobre uma rampa de 60o de in-
⇒ Δt = 13h20min
clinação e corre 20 m num trecho horizontal
antes de chegar em um loop circular, de pis-
ta sem atrito. Sabendo que o coeficiente de
Questão 4 atrito da rampa e do plano horizontal é 1/2,
assinale o valor do raio máximo que pode
Na figura, um ciclista percorre o trecho AB ter esse loop para que o carrinho faça todo o
com velocidade escalar média de 22,5 km/h e, percurso sem perder o contato com a sua
em seguida, o trecho BC de 3,00 km de exten- pista.

3. física 4
matéria escura de massa específica ρ > 0, que
se encontra uniformemente distribuída. Su-
ponha também que no centro dessa galáxia
haja um buraco negro de massa M, em volta
do qual uma estrela de massa m descreve
uma órbita circular. Considerando órbitas de
mesmo raio na presença e na ausência de ma-
téria escura, a respeito da força gravitacional
a) R = 8 3 m b) R = 4( 3 − 1) m
resultante F exercida sobre a estrela e seu
c) R = 8( 3 − 1) m d) R = 4(2 3 − 1) m
efeito sobre o movimento desta, pode-se afir-
e) R = 40( 3 − 1)/ 3 m mar que
a) F é atrativa e a velocidade orbital de m
alternativa C não se altera na presença da matéria escura.
Pelo teorema da energia cinética (TEC), a energia b) F é atrativa e a velocidade orbital de m é
cinética (Ec ’ ) do carrinho ao chegar ao loop é menor na presença da matéria escura.
dada por:
0 0
c) F é atrativa e a velocidade orbital de m é
R τ = ΔEc ⇒ P τ + f at. τ + N τ = E’c − Ec ⇒ maior na presença da matéria escura.
⎛ ⎞ d) F é repulsiva e a velocidade orbital de m é
H
⇒ mgH − ⎜ μmg cos 60o ⋅
⎜ o
+ μmgd ⎟ = E’c ⇒
⎟ maior na presença da matéria escura.
⎝ sen 60 ⎠
e) F é repulsiva e a velocidade orbital de m é
⎛1 1 2 menor na presença da matéria escura.
⇒ mg ⋅ 20 3 − ⎜ mg ⋅ ⋅ 20 3 ⋅ +
⎝2 2 3
1 ⎞ alternativa C
+ mg ⋅ 20 ⎟ = E’c ⇒ E’c = 20mg( 3 − 1)
2 ⎠
Sendo r o raio da órbita e M total a massa total que
Para situação de raio máximo, o peso deve atuar
atrai a estrela, a velocidade de órbita da estrela
como resultante centrípeta. Assim, temos:
GM total
m ⋅v2 vale v = . Dessa forma, na presença da
Rcp = P ⇒ = mg ⇒ v = Rg r
R
matéria escura, temos M total > M e, portanto, a
Assim, como no loop não há atrito, por conserva-
velocidade orbital v é maior do que na ausência
ção de energia entre o ponto mais baixo (1) e o
da matéria escura.
mais alto (2), com referência no solo, temos:
E1 = E 2 ⇒ E’c = E g + E” c ⇒
m 2
⇒ 20mg( 3 − 1) = mg(2R) + v ⇒
2 Questão 7
m
⇒ 20mg( 3 − 1) = mg(2R) + ( Rg ) 2 ⇒
2
Diagramas causais servem para represen-
⇒ R = 8( 3 − 1) m tar relações qualitativas de causa e efeito
entre duas grandezas de um sistema. Na
sua construção, utilizamos figuras como
Questão 6 para indicar que o aumento
da grandeza r implica aumento da grandeza s
Desde os idos de 1930, observações astronô-
micas indicam a existência da chamada ma- e para indicar que o aumen-
téria escura. Tal matéria não emite luz, mas to da grandeza r implica diminuição da gran-
a sua presença é inferida pela influência gra- deza s. Sendo a a aceleração, v a velocidade e
vitacional que ela exerce sobre o movimento x a posição, qual dos diagramas a seguir me-
de estrelas no interior de galáxias. Suponha lhor representa o modelamento do oscilador
que, numa galáxia, possa ser removida sua harmônico?

4. física 5
a) T
•0 <t <
4
b) T T
• 4
<t <
2
T 3T
c) • 2
<t <
4
3T
• 4
< t < 2T
d)
Considerando o módulo das grandezas, podemos
modelar o oscilador através do diagrama a seguir:
e)
Conseqüentemente, nenhuma das alternativas re-
presenta um modelamento adequado do oscilador
ver comentário harmônico.
Observação: se forem utilizados intervalos dife-
Considere o movimento harmônico de coordena-
rentes para trechos distintos do diagrama, as al-
da x, velocidade v e aceleração a representado
nos diagramas a seguir: ternativas B, C, D e E podem ser justificadas.
Questão 8
Uma balsa tem o formato de um prisma reto
de comprimento L e seção transversal como
vista na figura. Quando sem carga, ela sub-
merge parcialmente até a uma profundidade
h0 . Sendo ρ a massa específica da água e g a
aceleração da gravidade, e supondo seja man-
tido o equilíbrio hidrostático, assinale a carga
P que a balsa suporta quando submersa a
uma profundidade h1 .
2 2
a) P = ρgL( h1 − h0 ) sen θ
2 2
b) P = ρgL( h1 − h0 ) tan θ
2 2
c) P = ρgL( h1 − h0 ) sen θ / 2
2 2
Considerando o sinal das grandezas, podemos d) P = ρgL( h1 − h0 ) tan θ / 2
modelar o oscilador através dos diagramas a se- 2 2
e) P = ρgL( h1 − h0 ) 2 tan θ / 2
guir:

5. física 6
alternativa D
O volume da balsa, de comprimento L, imerso
quando está sem carga, é dado por:
Do movimento da bola 1, vem:
2x0 ⋅ h0
V0 = A0 ⋅ L ⇒ V0 = ⋅L ⇒ ’
v1 = v1 − gt 0 = 30 − 10t
2 ⇒ ⇒
2 θ ’2
v1 = 2
v1 − 2gy1 0 2 = 30 2 − 2 ⋅ 10y1
⇒ V0 = h0 ⋅ tg ⋅L
2
t = 3s
Então, o peso da balsa será dado por: ⇒
y1 = 45 m
2 θ
Pbalsa = E0 ⇒ Pbalsa = ρ ⋅ g ⋅ h0 ⋅ tg ⋅L
2 Analisando o movimento da bola 2, temos:
Logo, a carga P que a balsa suporta é: gt 2
y 2 = v 2 sen 30o t −
2 ⇒
P + Pbalsa = E ⇒ P = E − Pbalsa ⇒
x 2 = v 2 cos 30o t
2 θ 2 θ
⇒ P = ρ ⋅ g ⋅ h1 ⋅ tg ⋅ L − ρ ⋅ g ⋅ h0 ⋅ tg ⋅L ⇒
2 2 1 10 ⋅ 3 2
y 2 = 50 ⋅ ⋅3 − y 2 = 30 m
⇒
2 2 ⇒
2 2 θ
⇒ P = ρ ⋅ g ⋅ L(h1 − h0 ) tg 3 x 2 = 75 3 m
2 x2 = 50 ⋅ ⋅3
2
Da figura, a distância pedida é dada por:
d 2 = x 2 + (y1 − y 2 ) 2 ⇒
2
Questão 9 ⇒ d 2 = (75 3 ) 2 + (45 − 30) 2 ⇒
Considere hipoteticamente duas bolas lança- ⇒ d 2 = 16 875 + 225 ⇒ d = 17 100 m
das de um mesmo lugar ao mesmo tempo: a
bola 1, com velocidade para cima de 30 m/s, e
a bola 2, com velocidade de 50 m/s formando Questão 10
um ângulo de 30o com a horizontal. Conside-
rando g = 10 m/s2 , assinale a distância entre Considere uma bola de basquete de 600 g a
as bolas no instante em que a primeira alcan- 5 m de altura e, logo acima dela, uma de tênis
ça sua máxima altura. de 60 g. A seguir, num dado instante, ambas as
a) d = 6250 m bolas são deixadas cair. Supondo choques per-
feitamente elásticos e ausência de eventuais
b) d = 7217 m resistências, e considerando g = 10 m/s2 , assi-
c) d = 17100 m nale o valor que mais se aproxima da altura
máxima alcançada pela bola de tênis em sua
d) d = 19375 m ascensão após o choque.
e) d = 26875 m a) 5 m
b) 10 m
c) 15 m
alternativa C d) 25 m
Esquematizando as trajetórias das bolas, temos: e) 35 m

6. física 7
alternativa E 2ª situação:
p ’ 1
Por Torricelli, a velocidade da bola de tênis ao − 2 =
cair 5 m é dada por: p2 4 1 3
⇒ =− (II)
2
= 2
+ 2gΔy ⇒ v 2
=0 2
+ 2 ⋅ 10 ⋅ 5 ⇒ 1 1 1 f p2
v v0 = +
f p2 p2 ’
⇒ v = 10 m/s
Como as duas bolas percorrem a mesma distân- Igualando I e II, vem:
cia, suas velocidades são iguais. No entanto, as- 1 3
sim que a bola de basquete rebate elasticamente − =− ⇒ p 2 = 9p1
3p1 p2
no chão, o sentido de sua velocidade inverte, e
podemos considerar que as duas bolas sofrem
colisão elástica e direta. Adotando referencial Questão 12
para cima, do coeficiente de restituição, temos:
(v’ − V’) (v’ − V’)
e =− ⇒1 = − ⇒ Uma lâmina de vidro com índice de refração
(v − V) ( −10 − 10)
n em forma de cunha é iluminada perpendi-
⇒ V’ = v’ − 20 cularmente por uma luz monocromática de
Por conservação da quantidade de movimento, a comprimento de onda λ. Os raios refletidos
velocidade da bola de tênis após a colisão é dada pela superfície superior e pela inferior apre-
por:
sentam uma série de franjas escuras com es-
Q = Q’ ⇒ MV + mv = MV’ + mv’ ⇒
paçamento e entre elas, sendo que a m-ésima
⇒ 600 ⋅ 10 + 60 ⋅ ( −10) = 600 ⋅ (v’ − 20) + 60v’ ⇒
encontra-se a uma distância x do vértice.
⇒ v’ = 26,4 m/s
Assinale o ângulo θ, em radianos, que as su-
A altura máxima alcançada pela bola de tênis na
perfícies da cunha formam entre si.
ascensão após o choque é dada por:
v” 2 = v’ 2 − 2gh ⇒ 0 = 26,4 2 − 2 ⋅ 10 ⋅ h ⇒
⇒ h = 35 m
Questão 11
Um espelho esférico convexo reflete uma
a) θ = λ/2ne b) θ = λ/4ne
imagem equivalente a 3/4 da altura de um
c) θ = (m + 1)λ/2nme d) θ = (2m + 1)λ/4nme
objeto dele situado a uma distância p1 .
e) θ = (2m − 1)λ/4nme
Então, para que essa imagem seja refletida
com apenas 1/4 da sua altura, o objeto deve-
alternativa A
rá se situar a uma distância p2 do espelho,
dada por Do enunciado, podemos montar o esquema a se-
a) p2 = 9 p1 . b) p2 = 9 p1 / 4. guir:
c) p2 = 9 p1 / 7. d) p2 = 15 p1 / 7.
e) p2 = −15 p1 / 7.
alternativa A
Da equação de Gauss e da equação do aumento
linear, temos:
1ª situação:
p’ 3
− 1 = Supondo que o ângulo θ seja bem pequeno, po-
p1 4 1 1
⇒ =− (I) demos admitir que a diferença de caminhos per-
1 1 1 f 3p1
= + corridos pela luz que reflete na superfície superior
f p1 p1’ e inferior é dada por 2h.

7. física 8
Assim, temos: ras de apoio têm resistência e atrito desprezí-
h veis. Considerando que após deslizar durante
tg θ = ⇒ h = x tg θ ⇒ 2h = 2x tg θ
x um certo tempo a velocidade da haste perma-
Como a luz sofre inversão de fase na primeira re- nece constante em 2,0 m/s, assinale o valor
flexão e não sofre inversão de fase na segunda do campo magnético.
reflexão, para que ocorra franja escura (interfe- a) 25,0 T
λ
rência destrutiva), devemos ter 2h = m , com m b) 20,0 T
n
inteiro. c) 15,0 T
Das relações anteriores e da figura, vem: d) 10,0 T
x = me e) 5,0 T
2h = 2x tg θ
λ λ
λ ⇒ 2 me θ = m ⇒ θ =
2h = m n 2ne
n
θ = tg θ
alternativa E
Questão 13 Como o fluxo magnético é crescente, surge uma
corrente elétrica induzida no sentido horário de in-
Uma carga q distribui-se uniformemente na tensidade dada por:
superfície de uma esfera condutora, isolada, ε = B ⋅v ⋅ l
de raio R. Assinale a opção que apresenta a i =
R R
magnitude do campo elétrico e o potencial
Na situação de equilíbrio, a força magnética
elétrico num ponto situado a uma distância
(Fmag.) tem a mesma intensidade da componente
r = R/3 do centro da esfera.
P ⋅ sen 30o . Logo:
a) E = 0 V/m e U = 0 V 1
1 q Fmag. = P ⋅ sen 30o ⇒ B ⋅ i ⋅ l ⋅ sen 90o =
b) E = 0 V/m e U =
4 πε 0 R 1/2
1 3q = m ⋅ g ⋅ sen 30o
c) E = 0 V/m e U =
4 πε 0 R Substituindo a intensidade da corrente elétrica na
1 qr expressão anterior, vem:
d) E = 0 V/m e U = B ⋅v ⋅ l 2 ⋅1 ⋅1
4 πε 0 R2 B ⋅ ⋅l =m⋅g ⋅
1
⇒ B2 ⋅ =
1 rq R 2 2
e) E = eU=0V 1
4 πε 0 R3 = 5 ⋅ 10 ⋅ ⇒ B = 5,0 T
2
alternativa B
O campo elétrico dentro de uma esfera condutora Questão 15
em equilíbrio eletrostático é nulo e seu potencial
1 q A figura representa o campo magnético de
elétrico (U) é constante e dado por ⋅ .
4 πε0 R dois fios paralelos que conduzem correntes
elétricas. A respeito da força magnética re-
Questão 14 sultante no fio da esquerda, podemos afirmar
que ela
Uma haste metálica com 5,0 kg de massa e
resistência de 2,0 Ω desliza sem atrito sobre
duas barras paralelas separadas de 1,0 m, in-
terligadas por um condutor de resistência
nula e apoiadas em um plano de 30o com a
horizontal, conforme a figura. Tudo encon-
tra-se imerso num campo magnético B, per-
pendicular ao plano do movimento, e as bar-

8. física 9
a) atua para a direita e tem magnitude maior q = Q − Q0 ⇒ q =
ε ⋅ S ⋅V −
ε0 ⋅ S ⋅V
⇒
que a da força no fio da direita. d d
b) atua para a direita e tem magnitude igual
(ε − ε0 ) ⋅ S ⋅ V
à da força no fio da direita. ⇒ q =
d
c) atua para a esquerda e tem magnitude
maior que a da força no fio da direita.
d) atua para a esquerda e tem magnitude
igual à da força no fio da direita. Questão 17
e) atua para a esquerda e tem magnitude me-
nor que a da força no fio da direita. Luz monocromática, com 500 nm de compri-
mento de onda, incide numa fenda retangu-
alternativa D lar em uma placa, ocasionando a dada figura
de difração sobre um anteparo a 10 cm de
Da figura, é possível notar que existe um ponto à
distância.
esquerda dos fios onde o campo magnético resul-
tante é zero. Portanto as correntes têm sentidos
opostos. Sendo assim, os fios se repelem com a
mesma intensidade, obedecendo ao princípio da
ação e reação.
Questão 16
Na figura, o circuito consiste de uma bateria Então, a largura da fenda é
de tensão V conectada a um capacitor de pla- a) 1,25 μm. b) 2,50 μm. c) 5,00 μm.
cas paralelas, de área S e distância d entre si, d) 12,50 μm. e) 25,00 μm.
dispondo de um dielétrico de permissividade
elétrica ε que preenche completamente o es- alternativa C
paço entre elas. Assinale a magnitude da car-
Os mínimos de ordem m para uma difração de
ga q induzida sobre a superfície do dielétrico. mλ
fenda única são dados pela expressão y = D,
a
em que D é a distância da fenda ao anteparo e a
é a largura da fenda.
Da figura de difração, temos que o primeiro míni-
mo (m = 1) ocorre para | y | = 1 cm. Substituindo os
valores do enunciado, vem:
1 ⋅ 500
1= ⋅ 10 ⇒ a = 5 000 nm ⇒ a = 5,00 μm
a
a) q = εVd b) q = εSV / d
Questão 18
c) q = ( ε − ε0 )Vd d) q = ( ε − ε0 )SV / d
e) q = ( ε + ε0 )SV / d Dentro de um elevador em queda livre num
campo gravitacional g, uma bola é jogada
alternativa D para baixo com velocidade v de uma altura h.
Assinale o tempo previsto para a bola atingir
Com a inserção do dielétrico, a carga armazena-
o piso do elevador.
da nas placas do capacitor aumenta, e a carga q
induzida sobre a superfície do dielétrico pode ser a) t = v / g
encontrada pela diferença da carga final (Q) e a b) t = h / v
carga inicial (Q 0 ) nas placas do capacitor. c) t = 2h / g
Sabendo que em um capacitor plano de
placas paralelas a carga pode ser dada por d) t = ( v2 + 2 gh − v)/ g
ε ⋅ S ⋅ V , temos:
Q =
d e) t = ( v2 − 2 gh − v)/ g

9. física 10
alternativa B Da conservação da energia mecânica, adotando o
Em relação ao elevador, a bola realiza um MU. ponto mais baixo da trajetória como altura zero,
Admitindo que v seja a velocidade com que a bola temos a velocidade da massa m neste ponto
foi lançada em relação ao elevador, temos: como:
mv 2
h h mgL = ⇒ v = 2gL (II)
v = ⇒ t = 2
t v
De I e II, vem:
m ⋅ 2gL
Questão 19 T = + mg ⇒ T = 3mg
L
Um cubo de 81,0 kg e 1,00 m de lado flutua na
água cuja massa específica é ρ = 1000 kg/ m3 .
As questões dissertativas, numeradas
O cubo é então calcado ligeiramente para baixo de 21 a 30, devem ser resolvidas no
e, quando liberado, oscila em um movimento
caderno de soluções
harmônico simples com uma certa freqüência
angular. Desprezando-se as forças de atrito e
tomando g = 10 m/ s2 , essa freqüência angular
é igual a Questão 21
a) 100/9 rad/s. b) 1000/81 rad/s.
c) 1/9 rad/s. d) 9/100 rad/s. Um feixe de laser com energia E incide sobre
e) 81/1000 rad/s. um espelho de massa m dependurado por um
fio. Sabendo que o momentum do feixe de luz
alternativa A laser é E/c, em que c é a velocidade da luz,
A aceleração do sistema vem da variação do em- calcule a que altura h o espelho subirá.
puxo. O valor máximo da aceleração ocorre quan-
do o cubo estiver com o maior volume imerso na
água, então:
Rmáx. = ρ ⋅ g ⋅ hmáx. ⋅ l2
Rmáx. = m ⋅ γ máx. ⇒
2
γ máx. = hmáx. ⋅ ω
⇒ ρ ⋅ g ⋅ hmáx. ⋅ l2 = m ⋅ hmáx. ⋅ ω 2 ⇒
100 rad
⇒ 10 3 ⋅ 10 ⋅ 12 = 81 ⋅ ω 2 ⇒ ω=
9 s
Resposta
Questão 20
Do princípio da conservação da quantidade de
movimento, temos:
Considere um pêndulo simples de compri-
mento L e massa m abandonado da horizon- E ⎛ E’ ⎞
Qantes = Qdepois ⇒ = m ⋅ v + ⎜− ⎟ ⇒
c ⎝ c ⎠
tal. Então, para que não arrebente, o fio do
pêndulo deve ter uma resistência à tração ⇒ E’ = mvc − E
pelo menos igual a Do Princípio da Conservação da Energia Mecâni-
a) mg .b) 2mg. c) 3mg. d) 4mg. e) 5mg. ca logo após a incidência, vem:
mv 2 mv 2
alternativa C E = E’ + ⇒ E = mvc − E + ⇒
2 2
No ponto mais baixo da trajetória, a tração no fio 4E
⇒v2 + 2vc − =0
será máxima e expressa por: m
mv 2 mv 2 Como o sentido da velocidade do espelho coinci-
T −P = ⇒T = + mg (I)
L L de com a do feixe inicial, devemos ter v > 0.

10. física 11
Assim, temos: Na iminência de tombamento, o centro de massa
da chapa 1 deve coincidir com a extremidade di-
4E
v = c2 + −c reita da chapa 2.
m O centro de massa (C 2 ) das duas primeiras cha-
Conservando a energia mecânica do espelho, pas está a uma distância z da extremidade es-
vem: querda da segunda chapa dada por:
L
mv 2 v2 m⋅ +m⋅L
Ec = E g ⇒ = mgh ⇒ h = ⇒ z = 2 =
3L
2 2g 2m 4
3L L
2 Assim C 2 está a uma distância L − = da
⎛ 2 4E ⎞ 4 4
⎜ c + − c⎟ extremidade direita da chapa 2.
⇒ ⎝ m ⎠
h = Para três chapas, temos:
2g
Questão 22
Chapas retangulares rígidas, iguais e homo-
gêneas, são sobrepostas e deslocadas entre si,
formando um conjunto que se apóia parcial-
mente na borda de uma calçada. A figura Sendo C 3 o centro de massa das três primeiras
ilustra esse conjunto com n chapas, bem chapas e tomando esse ponto como pólo, o mo-
como a distância D alcançada pela sua parte mento das normais é nulo. Assim, do equilíbrio
suspensa. Desenvolva uma fórmula geral da dos momentos, vem:
máxima distância D possível de modo que o ⎛L ⎞ L
P ⎜ − x ⎟ = 2P ⋅ x ⇒ x =
⎝2 ⎠ 6
conjunto ainda se mantenha em equilíbrio. A
seguir, calcule essa distância D em função do Se fizermos o mesmo raciocínio para as quatro
comprimento L de cada chapa, para n = 6 uni- L
primeiras chapas, teremos x = .
dades. 8
Assim, a distância D4 para as quatro primeiras
chapas é dada por:
L L L L
D4 = + + +
2 4 6 8
Podemos montar, com base nessa expressão,
uma fórmula geral para n chapas:
L ⎛ 1 1 1 ⎞
Dn = ⎜1 + + + + ...⎟ ⇒
2 ⎝ 2 3 4 ⎠
Resposta L n
1
Para que o conjunto de chapas fique na iminência ⇒ Dn =
2
⋅ ∑n
1
de tombamento, o centro de massa das chapas
deve coincidir com a extremidade da calçada. Para n = 6 chapas, vem:
Para duas chapas, temos: 6
L 1
D6 =
2
⋅ ∑n ⇒
1
L ⎛ 1 1 1 1 1⎞
⇒ D6 = ⎜1 + + + + + ⎟ ⇒
2 ⎝ 2 3 4 5 6⎠
147L
⇒ D6 = = 1,225L
120

11. física 12
uma mola de comprimento L e constante k.
Questão 23 Calcule a deformação máxima sofrida pela
mola durante o acoplamento sabendo-se que
Em 1998, a hidrelétrica de Itaipu forneceu o foguete alcançou a mesma velocidade da es-
aproximadamente 87600 GWh de energia tação quando dela se aproximou de uma certa
elétrica. Imagine então um painel fotovoltai- distância d > L, por hipótese em sua mesma
co gigante que possa converter em energia órbita.
elétrica, com rendimento de 20%, a energia
solar incidente na superficie da Terra, aqui Resposta
considerada com valor médio diurno (24 h) Esquematizando a situação, sendo E a estação
aproximado de 170 W/m2 . Calcule: espacial e f o foguete, temos:
a) a área horizontal (em km2 ) ocupada pelos
coletores solares para que o painel possa ge-
rar, durante um ano, energia equivalente
àquela de Itaipu, e,
b) o percentual médio com que a usina operou
em 1998 em relação à sua potência instalada
de 14000 MW.
Vamos admitir que a massa da estação é muito
Resposta maior que a do foguete. Considerando que a acele-
a) Em um ano (8 760 h), a energia gerada pelos ração dele é constante e aponta para a estação es-
pacial, já que os dois corpos devem continuar se
coletores solares para cada m 2 pode ser dada
aproximando e que a força que produz a aceleração
por:
a atua até a máxima deformação da mola, ou seja,
ΔE = 0,2 ⋅ P ⋅ Δt = 0,2 ⋅ 170 ⋅ 8 760 = 297 840 Wh h = [d − (L − x)] , pelo teorema da energia cinética
Logo, a área (A) horizontal é encontrada por: (TEC), em relação à estação espacial, temos:
Energia (Wh) Área (m 2 ) 0
R τ = ΔEc ⇒Fτ + F τ = 0 ⇒
e
297 840 ⇒
1
87 600 ⋅ 109 kx 2
A ⇒F ⋅h − =0 ⇒
2
kx 2
⇒ ma[d − (L − x)] − =0 ⇒
⇒ A ≅ 3 ⋅ 10 8 m 2 ⇒ A ≅ 3 ⋅ 10 2 km 2 2
ΔE kx 2
b) A potência fornecida é dada por P = = ⇒ − max − ma(d − L) = 0 ⇒
Δt 2
87 600 GWh
= = 10 4 MW . ma ± m 2 a2 + 4 ⋅
k
⋅ ma(d − L)
8 760 h 2
⇒x =
O percentual médio ( η ) pode ser encontrado pela 2 ⋅
k
razão entre a potência fornecida e a potência ins- 2
talada, logo:
Como x deve ser positivo, vem:
104 MW
η= ⇒ η ≅ 71,43%
14 000 MW ma + m2 a2 + 2kma(d − L)
x =
k
Questão 24 Caso a força que produz a aceleração a cesse as-
sim que o foguete tocar a mola, teríamos
Num filme de ficção, um foguete de massa m h = d − L. Assim, vem:
segue uma estação espacial, dela aproximan-
do-se com aceleração relativa a. Para reduzir kx 2 2ma(d − L)
ma(d − L) − =0 ⇒ x =
o impacto do acoplamento, na estação existe 2 k

12. física 13
⎛ ⎞
Questão 25 ⎜ ⎟
GMm ⎜
− 1⎟ ⇒ f1z − f0z =
1
⇒ f1z − f0z =
R2 ⎜ ⎛ r ⎞
2 ⎟
Lua e Sol são os principais responsáveis pe- ⎜ ⎜1 + ⎟ ⎟
⎝⎝ R⎠ ⎠
las forças de maré. Estas são produzidas de-
vido às diferenças na aceleração gravitacio-
nal sofrida por massas distribuídas na Terra GMm ⎛ 2r ⎞ 2GMmr
= ⎜1 − − 1⎟ ⇒ f1z − f0z = −
em razão das respectivas diferenças de suas R2 ⎝ R ⎠ R3
distâncias em relação a esses astros. A figura
mostra duas massas iguais, m1 = m2 = m, Analogamente, para f2z − f0z , temos:
dispostas sobre a superfície da Terra em posi- GMm GMm
ções diametralmente opostas e alinhadas em f2z − f0z = − ⇒
(R − r) 2 R2
relação à Lua, bem como uma massa m0 = m
situada no centro da Terra. Considere G a ⎛ ⎞
⎜ ⎟
constante de gravitação universal, M a massa ⇒ f 2z − f0z =
GMm ⎜ 1
− 1⎟ ⇒ f2z − f0z =
da Lua, r o raio da Terra e R a distância en- R2 ⎜ ⎛ 2 ⎟
⎜ ⎜1 − r ⎞
⎟ ⎟
tre os centros da Terra e da Lua. Considere, ⎝⎝ R⎠ ⎠
também, f0 z , f1 z e f2 z as forças produzidas
pela Lua respectivamente sobre as massas GMm ⎛ 2r ⎞ 2GMmr
= ⎜1 + − 1⎟ ⇒ f2z − f0z =
m0 , m1 e m2 . Determine as diferenças R2 ⎝ R ⎠ R3
( f1 z − f0 z ) e ( f2 z − f0 z ) sabendo que deverá
1
usar a aproximação = 1 − αx, quan-
(1 + x )α Questão 26
do x << 1.
Para ilustrar os princípios de Arquimedes e
de Pascal, Descartes emborcou na água um
tubo de ensaio de massa m, comprimento L e
área da seção transversal A. Sendo g a acele-
ração da gravidade, ρ a massa específica da
água, e desprezando variações de temperatu-
ra no processo, calcule:
a) o comprimento da coluna de ar no tubo, es-
tando o tanque aberto sob pressão atmosféri-
ca Pa , e
Resposta b) o comprimento da coluna de ar no tubo, de
As forças gravitacionais que agem nas massas modo que a pressão no interior do tanque fe-
m0 = m1 = m2 = m devido à influência da Lua chado possibilite uma posição de equilíbrio
são dadas por: em que o topo do tubo se situe no nível da
água (ver figura).
GMm
f0z =
R2
GMm GMm
F = ⇒ f1z =
R2 (R + r) 2
GMm
f2z =
(R − r) 2
r
Considerando << 1 e usando a aproximação
R Resposta
fornecida, a diferença f1z − f0z é dada por:
a) A altura da coluna de ar l equivalente à altura
GMm GMm do tubo imerso na água é dada por:
f1z − f0z = − ⇒
(R + r) 2 R2 E = P ⇒ ρ ⋅ g ⋅ VLD = mg ⇒

13. física 14
m Resposta
⇒ρ⋅g ⋅A ⋅l =m⋅g ⇒ l =
ρ⋅A O trabalho realizado no processo AB é dado por:
Nessa condição, a pressão do ar no interior do 0
tubo será: τAB + τBC + τCA = τciclo ⇒ τAB − 40 = 30 ⇒
m
p = Pa + ρgl ⇒ p = Pa + ρ ⋅ g ⋅
ρA
⇒ ⇒ τ AB = 70 J
mg Como o processo AB é isotérmico, a variação da
⇒ p = Pa +
A energia interna é igual a zero. Do primeiro princí-
pio da termodinâmica, temos:
Da Lei de Boyle-Mariotte, vem:
0
⎛
p0V0 = p ⋅V ⇒ Pa ⋅ A ⋅ L = ⎜ Pa +
mg ⎞
⎟ ⋅ A ⋅ L’ ⇒
QAB = τAB + ΔU AB ⇒ QAB = 70 J
⎝ A ⎠
Pa ⋅ L
⇒
L’ =
mg Questão 28
Pa +
A
Três esferas condutoras, de raio a e carga
b) O comprimento da coluna de ar l’ no tubo para Q, ocupam os vértices de um triângulo eqüi-
que o mesmo fique em equilíbrio com o topo do látero de lado b >> a, conforme mostra a fi-
tubo no nível da água é: gura (1). Considere as figuras (2), (3) e (4),
em que, respectivamente, cada uma das esfe-
m
E = P ⇒ ρ ⋅ g ⋅ A ⋅ l’ = m ⋅ g ⇒ l’ = ras se liga e desliga da Terra, uma de cada
ρ⋅A
vez. Determine, nas situações (2), (3) e (4), a
carga das esferas Q1 , Q2 e Q3 , respectivamen-
te, em função de a, b e Q.
Questão 27
Três processos compõem o ciclo termodinâmi-
co ABCA mostrado no diagrama P × V da fi-
gura. O processo AB ocorre a temperatura
constante. O processo BC ocorre a volume
constante com decréscimo de 40 J de energia
interna e, no processo CA, adiabático, um
trabalho de 40 J é efetuado sobre o sistema.
Sabendo-se também que em um ciclo comple-
to o trabalho total realizado pelo sistema é de
30 J, calcule a quantidade de calor trocado
durante o processo AB.
Resposta
Como a carga Q1 está aterrada, o potencial elétri-
co resultante sobre ela é nulo, logo:
kQ kQ kQ1 2Qa
+ + = 0 ⇒ Q1 = −
b b a b

14. física 15
Para Q2 , temos: Esboçando o gráfico da expressão anterior, te-
kQ kQ1 kQ2 mos:
+ + =0 ⇒
b b a
Q 2Qa Q 2
⇒ − 2 + 2 = 0 ⇒ Q2 = 2Qa − Qa
b b a b 2 b
Para Q3 , vem:
kQ1 kQ2 kQ3
+ + =0 ⇒
b b a
Q3 2Qa 2Qa2 Qa
⇒ = 2 − + 2 ⇒
a b b3 b
3Qa2 2Qa3
⇒ Q3 = −
2
b b3
Questão 30
a2 a3
Observação: se considerarmos e despre-
b2 b3
Qa Considere um circuito constituído por um ge-
zíveis, teríamos Q2 = − e Q 3 = 0. rador de tensão E = 122,4 V, pelo qual passa
b
uma corrente I = 12 A, ligado a uma linha de
transmissão com condutores de resistência
Questão 29 r = 0,1Ω. Nessa linha encontram-se um mo-
tor e uma carga de 5 lâmpadas idênticas,
Um longo solenóide de comprimento L, raio
cada qual com resistência R = 99Ω, ligadas
a e com n espiras por unidade de comprimen-
em paralelo, de acordo com a figura. Determi-
to, possui ao seu redor um anel de resistência
nar a potência absorvida pelo motor, PM , pe-
R. O solenóide está ligado a uma fonte de cor-
las lâmpadas, PL , e a dissipada na rede, Pr .
rente I, de acordo com a figura. Se a fonte va-
riar conforme mostra o gráfico, calcule a ex-
pressão da corrente que flui pelo anel duran-
te esse mesmo intervalo de tempo e apresen-
te esse resultado em um novo gráfico.
Resposta
De acordo com a figura do enunciado, temos:
Resposta
A intensidade do campo de indução magnético
produzido pelo solenóide varia com o tempo se-
gundo a expressão B(t) = μ ⋅ I(t) ⋅ n. Assim, a Chamando a f.c.e.m. do motor de E’ e a resistên-
f.e.m. induzida é dada por: RL
cia equivalente às lâmpadas de R eq. = , pode-
n
ε = − d φ = −μ ⋅ n ⋅ π ⋅ a 2 ⋅ dI mos aplicar as leis de Kirchhoff como segue:
dt dt
I = i1 + i 2
Logo, a expressão da corrente que flui pelo anel é
dada por: −E + r ⋅ I + E’ + r ⋅ I = 0 ⇒
μ ⋅ n ⋅ π ⋅ a 2 dI r ⋅ i 1 + R eq. ⋅ i 1 + r ⋅ i1 − E’ = 0
i(t) = − ⋅
R dt

15. física 16
12 = i 1 + i 2 E’ = 120 V
⇒ −122,4 + 0,1 ⋅ 12 + E’ + 0,1 ⋅ 12 = 0 ⇒ i 1 = 6 A
0,1 ⋅ i 1 +
99
⋅ i 1 + 0,1 ⋅ i 1 − E ’ = 0 i2 = 6 A
5
Calculando as potências, temos:
PM = E’ ⋅ i 2 = 120 ⋅ 6 ⇒ PM = 720 W
2 99
PL = R eq. ⋅ i1 = ⋅ 6 2 ⇒ PL = 712,8 W
5
Pr = 2 ⋅ r ⋅ I 2 + 2 ⋅ r ⋅ i1 ⇒ Pr = 2 ⋅ 0,1 ⋅ 12 2 + 2 ⋅ 0,1 ⋅ 6 2 ⇒ Pr = 36 W
2
Física – domínio de Mecânica e Eletricidade
Com 80% das questões distribuídas entre Mecânica e Eletricidade, o
exame apresentou uma distribuição de assuntos com pouco equilíbrio.
Apesar disso, a tradição de prova exigente foi mantida. Infelizmente a
questão 7 não apresentou alternativa correta.