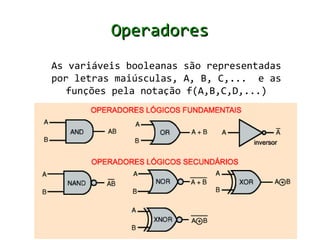
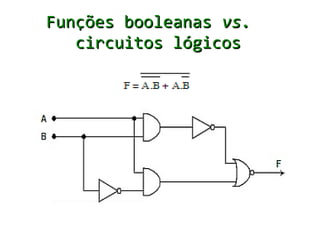
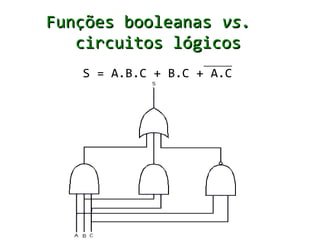
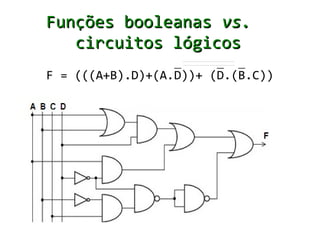
A álgebra de Boole estabeleceu um conjunto de símbolos matemáticos para representar a lógica formal e é aplicável ao projeto de circuitos lógicos digitais. Ela usa variáveis que podem assumir apenas os valores 0 ou 1 e operadores lógicos como AND, OR e NOT.