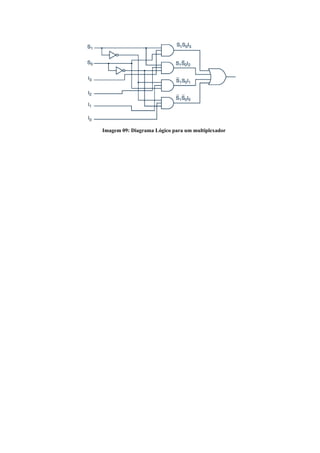
O documento discute os fundamentos da álgebra booleana e sua relação com portas lógicas e circuitos digitais. Apresenta os operadores lógicos básicos AND, OR e NOT e como eles são representados em tabelas-verdade. Explica como portas lógicas como NAND e NOR podem ser usadas para implementar esses operadores. Fornece exemplos de circuitos combinacionais como somadores, decodificadores e multiplexadores construídos a partir de portas lógicas.

1. ÁLGEBRA BOOLEANA E LÓGICA DIGITAL
AULA 04 – Arquitetura de Computadores
Gil Eduardo de Andrade
O conteúdo deste documento é baseado no livro “Princípios Básicos de Arquitetura e
Organização de Computadores” – Linda Null e Julia Labur.
1. Introdução
George Boole publicou em 1985 sua monografia com título “As Leis do Pensamento”
que criou um ramo da matemática chamado lógica simbólica ou álgebra booleana.
Nos itens a seguir será vista uma breve introdução sobre fundamentos de projeto lógico,
fornencendo uma cobertura mínima sobre álgebra booleana e seu relacionamento com portas
lógicas e circuitos digitais.
2. Álgebra Booleana
A Álgebra Booleana é uma álgebra para manipulação de objetos que podem assumir
apenas dois valores, normalmente “verdadeiro” ou “falso” ou “0” e “1” respectivamente.
Considerando o fato de que computadores são construídos como coleções de chaves que estão
“ligadas” ou “desligadas”, a álgebra booleana é uma maneira muito eficiente de representar
informação digital.
Os circuitos digitais utilizam tensões baixas e altas, essas tensões representam, para
nossa melhor compreensão, 0 e 1 respectivamente. Normalmente representamos o valor digital 0
como falso e o valor digital 1 como verdadeiro.
2.1. Expressões Booleanas
Além dos objetos binários, a álgebra booleana também possui operações que podem ser
realizadas sobre estes objetos, ou variáveis. Combinar variáveis e operadores dá origem a
expressões booleanas. Uma função booleana normalmente possui um ou mais valores de entrada
e fornece um resultado, baseado nesses valores de entrada, no conjunto {0, 1}.
Existem 3 operadores booleanos mais comuns, são eles AND, OR e NOT. Para
possibilitar o entendimento deles, é preciso um mecanismo que permita-nos examinar seus
comportamentos. Um operador booleano pode ser completamente descrito usando-se uma tabela
que relaciona suas entradas, todos os possíveis valores delas e os valores resultantes da operação
para as combinações destas entradas. Esta tabela é denominada tabela-verdade.
Sendo assim vamos examinar os operadores booleanos AND, OR e NOT para observar
como cada um é representado usando álgebra booleana e tabelas-verdade.
2.2. Operador Lógico AND
O operador lógico AND é, geralmente, representado por um ponto ou simplesmente por
nenhum símbolo. Como exemplo podemos utilizar a expressão booleana xy que é equivalente à
expressão x · y que é lida como “x e y”. O comportamento deste operador é representado pelas
linhas da tabela-verdade abaixo.
Tabela 01: Tabela-verdade do operador lógico AND

2. O resultado de uma expressão xy é 1, somente quando as suas entradas são 1, e 0, caso
contrário. Cada linha da tabela representa uma expressão booleana diferente, e todas as possíveis
combinações de valores para x e y são apresentadas pelas linhas da tabela.
2.3. Operador Lógico OR
O operador lógico OR é, geralmente, representado por um sinal de mais. Sendo assim, a
expressão x + y é lida como “x ou y”. O comportamento deste operador é representado pelas
linhas da tabela-verdade abaixo.
Tabela 02: Tabela-verdade do operador lógico OR
O resultado de x + y é 0 somente quando ambos os valores de entrada são 0. A expressão
x + y é frequentemente referida como uma soma booleana.
2.4. Operador Lógico NOT
O operador lógico NOT é, geralemente, representado por um traço superior ou uma
apóstrofe. Sendo assim, tanto quanto 'x são lidos como “NOT x”. O comportamento deste
operador é representado pelas linhas da tabela-verdade abaixo.
Tabela 03: Tabela-verdade do operador lógico NOT
Após essa visão geral sobre os operadores AND, OR e NOT é possível entender que a
álgebra booleana lida com variáveis binárias e operações lógicas sobre estas variáveis.
Combinando esses dois conceitos, podemos examinar expressões booleanas compostas de
variáveis booleanas e vários operadores lógicos. Como por exemplo, a função booleana:
que é representada por uma expressão booleana envolvendo as três variáveis booleanas x, y, z e
os operadores lógicos OR, NOT e AND. Lembrando que as regras de precedência (indica qual
operador aplicar primeiro) dão ao NOT a prioridade mais alta, seguido pelo AND e só depois
OR.
Resolvendo a nossa função anterior F(x,y,z), teríamos primeiramente que negar y, depois
efetuar o operador AND da negação de y com z e, por último, efetuar o OR deste resultado com
x. A tabela-verdade para função F(x,y,z) é apresentado abaixo.

3. Tabela 04: Tabela-verdade para função F(x,y,z)
3. Portas Lógicas
Os operadores lógicos AND, OR e NOT, discutidos até o momento, estão sendo
representados de forma abstrata, pelo uso de tabelas-verdade e expressões booleanas. Contudo os
componentes físicos reais, ou circuitos digitais, tais como aqueles que realizam operações
aritméticas ou fazem escolhas em um computador, são construídos a partir de diversos elementos
primitivos denominados portas. Estas portas implementam cada uma das funções lógicas básicas
que foram discutidas.
3.1. Símbolo para as portas lógicas
Inicialmente serão analisadas as três portas mais simples, correspondentes aos operadores
lógicos AND, OR e NOT. O comportamento funcional de cada um destes operadores já foi
discutido então agora teremos foco nas suas representações que são apresentadas logo abaixo.
Imagem 01: Representação das três portas básicas
Outra porta comum é a porta denominada OR-exclusivo (XOR), representada pela
expressão booleana:
O XOR é falso quando ambos os valores de entrada são iguais e verdadeiro caso
contrário. A figura abaixo apresentada a tabela-verdade do XOR, especificando seu
comportamento, bem como a representação desta porta lógica.

4. Imagem 02: (a) Tabela-verdade XOR – (b) Representação lógica XOR
3.2. Portas Universais
Existem também outras portas comuns, são elas a porta NAND e NOR, que produzem
saídas complementares as portas AND E OR, respectivamente. Cada porta possui dois símbolos
lógicos distintos que podem ser usados para a representação da porta. As tabelas-verdade e
representção lógica são apresentados logo abaixo.
Imagem 03: Tabela-verdade NAND – Representação lógica NAND
Imagem 04: Tabela-verdade NOR – Representação lógica NOR
Possivelmente, você pode estar se perguntando por que utilizar portas como NAND ou
NOR, a reposta é simples, existem dois motivos para isso: o primeiro é que o custo para
fabricação de uma porta NAND/NOR é mais barato em relação a outras portas, e o segundo é
que pode-se construir qualquer circuito usando apenas portas NAND/NOR.
3.3. Portas com múltiplas entradas
Até o momento haviamos utilizado apenas portas com duas entradas, contudo, portas não
são limitadas a apenas esses dois valores, existem muitas variações no número e nos tipos de
entradas e saídas permitidas para diversas portas. Por exemplo podemos implementas as portas
AND, OR e NOT com a combinação de portas NAND, como é apresentado logo abaixo.
Imagem 05: Implementando portas AND, OR e NOT apenas com portas NAND

5. 4. Componentes Digitais
Observando um computador por dentro é possível constatar que existe muitos
componentes digitais que constituem o sistema, e pouco sabemos sobre eles. Porém, na verdade,
o um computador é constituído por uma coleção de portas que são conectadas por fios (trilhas)
que atuam como caminhos de sinais. Essas coleções ou blocos de construção são,
surpreendentemente, inteiramente construídos usando as operações básicas AND, OR e NOT.
4.1. Circuitos Integrados
Computadores são compostos por diversos componentes digitais conectados por fios
(“trilhas”). Como um bom programa, o hardware real de um coputador usa coleções de portas
para criar módulos maiores, os quais são utilizado para implementar diversas funções.
Geralmente portas não são vendidas individualmente, mas sim em unidades denominadas
circuitos integrados (CIs). Um chip (cristal de silício semicondutor) é um pequeno dispositivos
eletrônico que consiste de um conjunto de outros componentes eletrônicos necessários
(transistores, resistores e capacitores) para implementar diversas portas.
Abaixo é apresentado o circuito integrado de uma porta lógica NAND.
Imagem 06: Arquitetura – Circuito Integrado (CI) da porta NAND
5. Exemplos de circuitos combinacionais
→ Semi-Somador
Imagem 07: Diagrama Lógico para um semi-somador

6. → Somador Completo
Imagem 08: Diagrama Lógico para um somador completo
→ Decodificador
Quando um computador reecebe um endereço, ele primeiro deve saber determinar qual
chip deve usar; então ele deve encontrar o endereço real nesse chip específico. Considerando a
utilização de 16 bits e que os 2 bits mais a esquerda são usados para selecionar o chip e os outros
14 para encontrar o enderelo no chip usado. Esses 2 bits de mais alta ordem são na verdade
usados como entradas em um decodificador, de modo a determinar qual chip deve ser ativado
para leitura ou escrita.
Se considerarmos como exemplo que os 2 bits são 00, o chip 0 deve ser ativado, caso os 2
sejam 11, o chip 3 deve ser ativado. Sendo assim a saída do decodificador é usada para ativar um
e apenas um chip.
Imagem 09: Diagrama Lógico para um decodificador
→ Multiplexador
Outro circuito combinacional comum é o multiplexador. Este circuito seleciona
informação binária de uma das várias linhas de entrada e direciona para uma única linha de
saída. A seleção de uma linha de entrada particular é controlada por um conjunto de variáveis de
seleção, ou linhas de controle.
Um exemplo da utilização de multiplexação é a transmissão do sinal de internet ADSL,
que utiliza uma faixa de freqüências (entrada dados) não utilizadas pela voz (entrada de voz) nas
linhas telefônicas para transmitir dados.

7. Imagem 09: Diagrama Lógico para um multiplexador