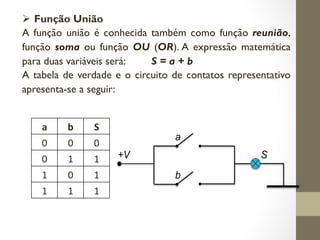
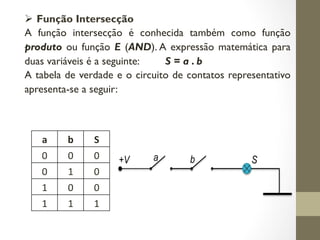
O documento aborda a álgebra booleana e sua aplicação em circuitos digitais, explicando operações lógicas básicas como AND, OR, e NOT. São introduzidos conceitos de funções e expressões booleanas, além de tabelas-verdade que relacionam variáveis e resultados. O texto também discute postulados, propriedades e teoremas essenciais para entender a lógica matemática subjacente à eletrônica digital.

1. Disciplina: Electrónica Digital
Docente: Prof. Doutor Manuel Zunguze

2. 1. Equações Booleanas e Circuitos lógicos básicos
A álgebra booleana foi criada pelo matemático inglês George
Boole (1815-1864).
A álgebra booleana é uma forma de utilizar técnicas algébricas
para lidar com expressões cujas variáveis trabalham somente
com dois valores: falso (0) ou verdadeiro (1). Atualmente,
todos os sistemas digitais são baseados nela, relacionando os
níveis lógicos 0 (falso) e 1 (verdadeiro) com a passagem ou
ausência de corrente eléctrica.
Os seus elementos da álgebra de Boole, a princípio, não tem
significado numérico.
1.1. A álgebra de Boole e os Circuitos Digitais

3. Se x é uma variável boleana então:
Se x ≠ 0 ⇒ x = 1
Se x ≠ 1 ⇒ x = 0
Operações
Postulados
São definidas algumas operações elementares na álgebra boleana:
Operação “Não” (NOT)
Operação “E” (AND)
Operação “Ou” (OR)
Operação “Ou-Exclusivo” (Exclusive-Or ou XOR)
ØOperação “Não” (NOT)
• operador barra –
• 0 = 1
• 1 = 0

4. Ø Operação “E” (AND)
— operador ponto .
— 0 . 0 = 0
— 0 . 1 = 0
— 1 . 0 = 0
— 1 . 1 = 1
ØOperação “Ou” (OR)
— operador +
— 0 + 0 = 0
— 0 + 1 = 1
— 1 + 0 = 1
— 1 + 1 = 1
ØOperação “Ou-Exclusivo” (XOR)
— operador ⊕
— 0 ⊕ 0 = 0
— 0 ⊕ 1 = 1
— 1 ⊕ 0 = 1
— 1 ⊕ 1 = 0

5. 1.2NoçãodeFunçõesLógicasOuBooleanas
Os termos função e expressão são muitas vezes considerados
sinónimos, entretanto, matematicamente eles representam
entidades diferentes.
ØUma expressão é uma combinação de números, operadores e
variáveis, compondo somente um objecto.
ØUma função é uma generalização da noção comum de fórmula
matemática. Funções descrevem as relações matemáticas entre
dois objetos, x e y = f(x), onde o objeto x é chamado de
argumento da função f, o objeto y que depende de x é chamado
imagem de x por f e a função f é uma expressão contendo o
argumento x como variável.

6. Para a álgebra booleana estes conceitos também são válidos, e
portanto, podemos ter funções e expressões booleanas.
As funções e expressões booleanas são formadas somente pelos
números 0 e 1, pelos operadores lógicos descritos
anteriormente e por variáveis booleanas. Uma ou mais variáveis
e operadores podem ser combinados formando uma função
lógica.
A Tabela 1 mostra alguns exemplos de expressões e funções
booleanas.

7. 1.3Tabela-Verdade
Os resultados de uma função lógica podem ser expressos numa
tabela relacionando todas as combinações possíveis dos valores
que suas variáveis podem assumir e seus resultados
correspondentes: a Tabela-Verdade.
A B Z = f (A,B)
0 0 0
0 1 1
1 0 1
1 1 1
Lista das
combinações
possíveis dos
estados das
variáveis de
entrada
Variáveis Função Lógica
Resultados da
função lógica para
cada combinação
dos estados de
entrada
Na Tabela-Verdade acima a função lógica Z possui duas variáveis
A e B, sendo Z = f(A, B) = A + B

8. 1.4FunçõesBooleanasBásicas
As funções booleanas ou logicas básicas elementares são:
• Função Igualdade
• Função União
• Função Intersecção
• Função Negação
Ø Função Igualdade
A função igualdade é a mais elementar e intervém
somente uma variável. A expressão matemática é a
seguinte: S = a
A tabela de verdade, assim como a sua materialização
mediante contatos, apresenta-se a seguir:
a S
0 0
1 1
a=0
a=1
S=0
S=1

9. Ø Função União
A função união é conhecida também como função reunião,
função soma ou função OU (OR). A expressão matemática
para duas variáveis será: S = a + b
A tabela de verdade e o circuito de contatos representativo
apresenta-se a seguir:
a b S
0 0 0
0 1 1
1 0 1
1 1 1

10. Ø Função Intersecção
A função intersecção é conhecida também como função
produto ou função E (AND). A expressão matemática para
duas variáveis é a seguinte: S = a . b
A tabela de verdade e o circuito de contatos representativo
apresenta-se a seguir:
a b S
0 0 0
0 1 0
1 0 0
1 1 1

11. 1.5OutrasFunçõesBásicasImportantes
Ø Função Negação
A função negação é também conhecida como complemento
ou função NAO (NOT). A sua expressão matemática é: S = a
A tabela de verdade apresenta-se na figura a seguir:
a S
0 1
1 0
Outras funções básicas importantes são:
• Função NAND: que é a função AND negada
• Função NOR: que e a função OR negada
• Função exclusive OR.

12. Denominação Tabela Função
NAND
S = a . b
NOR
S = a + b
Exclusive OR
S = a . b + a . B
S = a ⊕ b
a b S
0 0 1
0 1 1
1 0 1
1 1 0
a b S
0 0 1
0 1 0
1 0 0
1 1 0
a b S
0 0 0
0 1 1
1 0 1
1 1 0

13. • Postulado 1
A soma logica de uma variável mais um 1 logico equivale a
um 1 logico.
a + 1 = 1
1.6 Postulados, Propriedades e Teoremas da Álgebra de Boole
Postulados
• Postulado 2
A soma logica de uma variável mais um 0 logico equivale ao
valor da variável.
a + 0 = a
• Postulado 3
O produto logico de uma variável por um 1 logico e igual ao
valor da variável.
a . 1 = a

14. • Postulado 4
O produto logico de uma variável por um 0 logico e igual a 0.
a . 0 = 0
• Postulado 5
A soma logica de duas variáveis iguais equivale ao valor dessa
variável.
a + a = a
• Postulado 6
O produto logico de duas variáveis iguais equivale ao valor
dessa variável.
a . a = a
• Postulado 7
A soma logica de uma variável mais a mesma variável negada
equivale a um 1 logico.
a + a = 1

15. Sendo A, B e C variáveis boleanas
ØPropriedade Comutativa
• A . B = B .A
• A + B = B + A
• A ⊕ B = B ⊕ A
ØPropriedade Associativa
• ( A . B ) . C = A . ( B . C ) = A . B . C
• ( A + B ) + C = A + ( B + C ) = A + B + C
• ( A ⊕ B ) ⊕ C = A ⊕ ( B ⊕ C ) = A ⊕ B ⊕ C
Propriedades
• Postulado 8
O produto logico de uma variável pela mesma variável negada
equivale a um 0 logico.
a . a = 0
• Postulado 9
Se uma variável e negada duas vezes, esta nao varia.
a = a

16. ØPropriedade Distributiva
• A . (B + C ) = A . B + A . C
• A + B . C = (A + B) . (A + C)
ØTeorema 1. Leis de Absorção
• A + A.B = A
Ø Teorema 2
• A + A . B = A + B
• (A + B) . B = A . B
Ø Teorema 3. Leis de De Morgan
• A+B=A . B
• A.B=A+B
Teoremas

17. ØIdentidades importantes
1.7 Identidades
a.b+ a.b = a
a + b
( ). a + b
( )= a
a. a + b
( )= a
a. a + b
( )= a.b
a.b+ a.c = a +c
( ). a + b
( )
0 =1
1 = 0
a = a
ØNOT
a.1= a
a.0 = 0
a.a = a
a.a = 0
ØAND
ØOR
a +1=1
a + 0 = a
a + a = a
a + a =1

18. Exercícios
1. Levante as tabela-verdade das expressões:
f X ,Y ,Z
( )= X +Y
( ) XY + Z
( )
f A,B,C
( )= A + B
( ) A + AB
( ) A + B + ABC
( )
f A,B,C ,D
( )= A + B +C
( ) B +C + D
( )