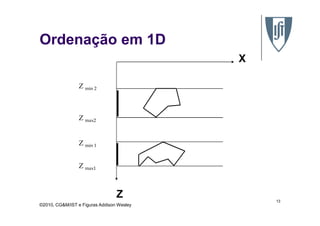
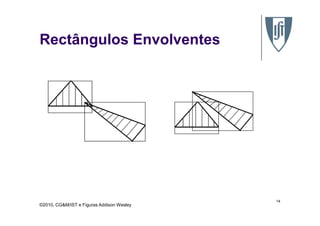
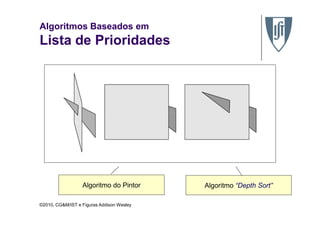
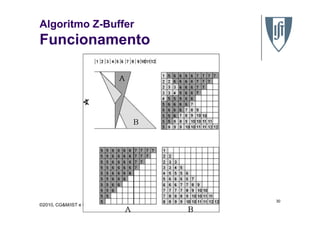
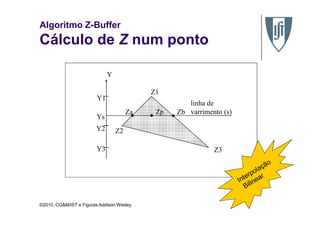
O documento discute algoritmos de remoção de superfícies ocultas em computação gráfica, comparando abordagens baseadas em lista de prioridades e algoritmos de varredura de linha. Especificamente, descreve o algoritmo de ordenação em profundidade, o algoritmo do pintor e o algoritmo Z-buffer, explicando como cada um determina a ordem de desenho dos objetos para assegurar a remoção correta de superfícies ocultas.


































![Exemplo
B
C
D
E
F
Y
β
ϕ
ϕ + 1
ϕ + 2
©2010, CG&M/IST e Figuras Addison Wesley
43
A
F
X
α
PT: AET:
( ABC )
( DEF )
ET:
[A,B]
[F,D]
[A,C]
[D,E]
[F,E]
[C,B]
.........
scan-line β :
scan-line α:
scan-lines ϕ, ϕ+1:
scan-line ϕ+2:
[A,B] [A,C]
[A,B] [A,C] [F,D] [F,E]
[A,B] [D,E] [C,B] [F,E]
[A,B] [C,B] [D,E] [F,E]](https://image.slidesharecdn.com/aula19-visibilidade-150722212208-lva1-app6891/85/Aula19-visibilidade-42-320.jpg)


![Exemplo
B
C
D
EY
β
ϕ
ϕ + 1
ϕ + 2
©2010, CG&M/IST e Figuras Addison Wesley
47
A
F
X
α
β
PT: AET:
( ABC )
( DEF )
ET:
[A,B]
[F,D]
[A,C]
[D,E]
[F,E]
[C,B]
.........
scan-line β :
scan-line α:
scan-lines ϕ,
ϕ+1:
scan-line
ϕ+2:
[A,B] [A,C]
[A,B] [A,C] [F,D] [F,E]
[A,B] [D,E] [C,B] [F,E]
[A,B] [C,B] [D,E] [F,E]](https://image.slidesharecdn.com/aula19-visibilidade-150722212208-lva1-app6891/85/Aula19-visibilidade-46-320.jpg)