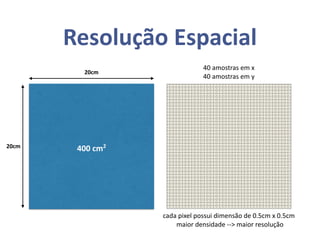
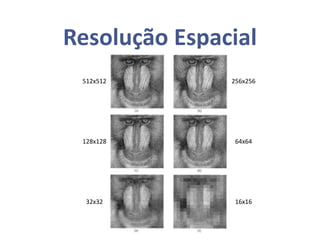
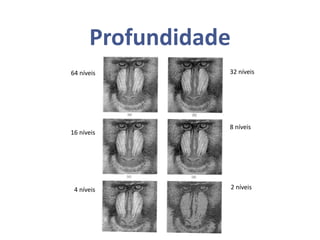
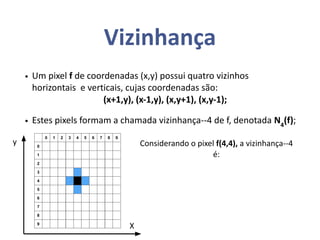
O documento aborda o processamento de imagens, explorando conceitos como resolução espacial e profundidade de pixels, que impactam na qualidade da imagem. Também discute a conectividade entre elementos, a definição de bordas e interiores, além de operações aritméticas e lógicas aplicadas em imagens. Exemplos e definições matemáticas são fornecidos para ilustrar as relações entre pixels e suas aplicações práticas.

1. Processamento de Imagens
de Computação Gráfica
Elementos das
Imagens Digitais
Profª. Ma. Layse Souza

2. Resolução Espacial
• O processo de resolução espacial está
associada à densidade de pixels da imagem,
ou seja, quanto maior a densidade de pixels
em uma imagem, maior será a resolução dela;
• A resolução de uma imagem deve ser
escolhida de modo a atender ao grau de
detalhes que devem ser discerníveis na
imagem;

3. Resolução Espacial
400 cm2
20cm
20cm
20 amostras em x
20 amostras em y
cada pixel possui dimensão de 1cm x 1cm

4. Resolução Espacial
400 cm2
20cm
20cm
40 amostras em x
40 amostras em y
cada pixel possui dimensão de 0.5cm x 0.5cm
maior densidade --> maior resolução

5. Resolução Espacial
400 cm2
20cm
20cm
10 amostras em x
10 amostras em y
cada pixel possui dimensão de 2cm x 2cm
menor densidade --> menor resolução

6. Resolução Espacial
512x512 256x256
128x128 64x64
32x32 16x16

7. Profundidade
• O número de níveis de cinza de quantização da imagem
f(x,y) é normalmente representado em potência de 2, ou
seja, L = 2b
, onde L é o número de níveis de cinza da
imagem e b é chamado de profundidade da imagem;
• Exemplo:
Se L = 256 (níveis de 0 a 255), isto significa que são
necessários 8 bits (256 = 28
) por pixel para armazenar uma
imagem;

8. Profundidade
64 níveis 32 níveis
16 níveis
8 níveis
4 níveis 2 níveis

9. Profundidade
• Com a informação da profundidade de uma
imagem é possível saber quantos bytes são
necessários para armazenar uma imagem;

10. Profundidade
• Considere umaimagem digital f(x, y),
com M = 640, N = 400 e L = 32. Qual o
espaço (em bytes) necessários para
armazená--la?

11. Profundidade
• Considere umaimagem digital f(x,y), com
M = 1024,N = 720 e L = 512. Qual o
espaço (em bytes) necessário para
armazená--la?

12. Relacionamentos entre
elementos de uma imagem

13. Vizinhança
0 1 2 3 4 5 6 7 8 9
0
1
2
3
4
5
6
7
8
9
• Um pixel f de coordenadas (x,y) possui quatro vizinhos
horizontais e verticais, cujas coordenadas são:
(x+1,y), (x-1,y), (x,y+1), (x,y-1);
• Estes pixels formam a chamada vizinhança--4 de f, denotada N4
(f);
Considerando o pixel f(4,4), a vizinhança--4
é:
X
y

14. Vizinhança
0 1 2 3 4 5 6 7 8 9
0
1
2
3
4
5
6
7
8
9
• Os quatro vizinhos diagonais de f são os pixels de coordenadas:
(x - 1, y - 1), (x - 1, y + 1), (x + 1, y - 1) e (x + 1, y + 1)
que constituem o conjunto Nd
(f)
• Os pixels vermelhos representam o Nd
(f) do pixel (4,4)
Sendo assim, os vizinhos diagonais de f(4,4)
são:

15. Conectividade
• A conectividade entre os elementos de uma imagem tem
importante aplicação quando queremos estabelecer limites
de objetos e componentes de regiões em uma imagem;
• Para determinar se dois elementos são conexos é necessário
determinar se eles são vizinhos segundo uma vizinhança
adotada e se os elementos satisfazem um determinado
critério de similaridade (intensidade, cor, textura e entre
outros);
• Em uma imagem binária, em que os pixels podem assumir os
valores de 0 ou 1, dois pixels podem ter vizinhança--4 , mas
somente serão considerados conexos se possuírem o
mesmo valor;

16. Adjacência
• Um elemento f1
é adjacente a um elemento
f2
se eles forem conexos de acordo com o
tipo de vizinhança adotado;
• Dois subconjuntos de pixels S1
e S2
são
adjacentes se pelo menos um elemento em
S1
for adjacente aalgum elementoem S2
;

17. Adjacência
V -> o conjunto de valores de intensidade utilizados para definir a adjacência
• adjacência-4: dois pixels p e q com valores pertencendo a V são
adjacentes se q estiver no conjunto N4(p) ;
• adjacência-8: dois pixels p e q com valores pertencendo a V são
adjacentes se q estiver no conjunto N8(p) ;
• adjacência-m: dois pixels p e q com valores pertencendo a V são
adjacentes se:
a) q estiver em Nq(p) ; ou
b) q estiver em ND(p) e o conjunto N4(p)∩N4(q) não contiver
nenhum pixel cujos valores pertençam a V

18. Adjacência
a) Um arranjo de pixels
b) Pixels que são adjacentes-8 (linhas tracejadas)
c) Adjacência-m
d) Duas regiões de 1s que são adjacentes se a adjacência-8 for utilizada

19. Caminho
• Um caminho na imagem do pixel (x1
, y1
) a um pixel (xn
, yn
) é
uma sequência de pixels distintos com coordenadas (x1
, y1
),
(x2
, y2
), … , (xn
,yn
), onde n é o comprimento do caminho, e (xi
,
yi
) e (xi+1
. yi+1
) são adjacentes, tal que i = 1, 2, … n--1;
• Se a relação de conectividade considerar a vizinhança--4, então
existe um caminho--4; para vizinhança--8, tem--se um
caminho--8;
0 1 2 3 4 5 6
0
1
2
3
4
5
6
0 1 2 3 4 5 6
0
1
2
3
4
5
6
caminho-- caminho--

20. Componentes
Conexos
• Um subconjunto de elementos C da imagem que são conexos entre
si é chamado de componente conexo;
• Dois elementos f1
e f2
são conexos se existir um caminho de f1
a f2
contido em C; 0 1 2 3 4 5 6 7 8 9 10 11 12 13
0
1
2
3
4
5
6
7
8
9
10
11
12
13
A imagem bidimensional ao lado contém três
componentes conexos se considerarmos a
vizinhança--4 e dois componentes se
considerarmos
a vizinhança--8.

21. Borda e
Interior
• A borda de um componente conexo S em uma
imagem bidimensional é o conjunto de pixels
pertencentes ao componente e que possuem
vizinhança--4 com um ou mais pixels externos a S;
• Logo, a borda corresponde ao conjunto de pontos
no contorno do componente conexo;
• O interior é o conjunto de pixels S que não estão
em sua borda;

22. Borda e
Interior
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10
• Considere a imagem bidimensional a seguir e o componente S
(pixels em preto);
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10

23. Borda e
Interior
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10
• Sendo assim, na imagem a seguir, os pixels em preto são a borda da
imagem e os pixels em cinza correspondem ao interior da imagem.

24. Medidas de
Distância
• Muitas aplicações necessitam da noção de distância entre
pixels ou componentes de uma imagem
• Existem várias equações para determinar esta distância
• Distância Euclidiana
• Distância D4
• Distância D8

25. Distância Euclidiana
• Adistância euclidiana entre f1
e f2
é definida
como:
DE
(f1
, f2
) = sqrt((x1
-- x2
)2
+ (y1
-- y2
)2
)

26. Distância D4
• Adistância D4,
também denominada de
city--block,entre f1
e f2
é dada por:
D4
(f1
,f2
) = |x1
-- x2
| + |y1
-- y2
|

27. Distância D8
• Adistância D8,
também denominada de
chessboard, entre f1
e f2
é dada por:
D8
(f1
,f2
) = max(|x1
-- x2
|,|y1
-- y2
|)

28. Distância
• Na distância D4
, os pixels com distância 1
são os pixels de vizinhança--4de um
determinado pixel central;
• A distância D4
entre dois pixels f1e f2é igual
ao comprimento do caminho mais curto
entre esses pixels, considerando--se a
vizinhança--4;

29. Distância
• Na distância D8
, os pixelscom distância
1 são os pixels de vizinhança--8 de
um determinado pixel central;
• A distância D8
entre dois pixelsf1 e f2 é
igual ao comprimento do caminho mais
curto entre esses pixels considerando-se
a vizinhança -4;

30. Operações Lógicas e
Aritméticas
• Operações lógicas e aritméticas podem ser
utilizadas para modificar imagens;
• Apesar de ser um técnica simplesde
processamento, há uma grande
variedade de aplicaçõesem que tais
operações podemproduzir resultados
de interesse prático;

31. Operações Lógicas e
Aritméticas
• Dadas duas imagens, f1
e f2
, as operações aritméticas mais
comuns entre dois pixels f1
(x,y) e f2
(x,y) são a adição,
subtração, multiplicação e divisão, definidas como a seguir:
Adição f1
(x,y) + f2
(x,y)
Subtração f1
(x,y) -- f2
(x,y)
Multiplicação f1
(x,y).f2
(x,y)
Divisão f1
(x,y) / f2
(x,y)

32. Operações Lógicas e
Aritméticas
• Tais operações podem produzir valores fora do
intervalo de níveis de cinza das imagens
originais. Sendo assim, devemos ter cuidado
para contornar essa situação;
• Deve--se evitar valores maiores na soma e
multiplicação, valores negativos na subtração;
• A divisão pode produzir valores fracionários ou
divisão por zero;

33. Operações Lógicas e
Aritméticas
• Dentre as principais aplicações temos:
• A adição pode ser utilizada para sobrepor o conteúdo
de uma imagem na outra ou para remoção de ruídos
pelo cálculo da média de imagens;
• A subtração pode ser utilizada para identificar
diferenças entre imagens;
• A multiplicação e divisão pode ser utilizado no ajuste de
brilho, eventualmente necessário para corrigir
problemas que possam surgir durante o processo de
aquisição de imagens;

34. Operações Lógicas e
Aritméticas
As principais operações lógicas são aplicadas somente em
imagens binárias. As principais são mostradas a seguir:
•
• Para as imagens binárias adotamos que pixels com valores
iguais a 0 (preto) pertencem aos objetos e pixels com
valores iguais a 1 (branco) correspondem ao fundo;
AND f1
(x,y) AND f2
(x,y)
OR f1
(x,y) OR f2
(x,y)
XOR f1
(x,y) XOR f2
(x,y)
NOT NOT(f1
(x,y))

35. Referência
• Cap. 2 do livro do Pedrini