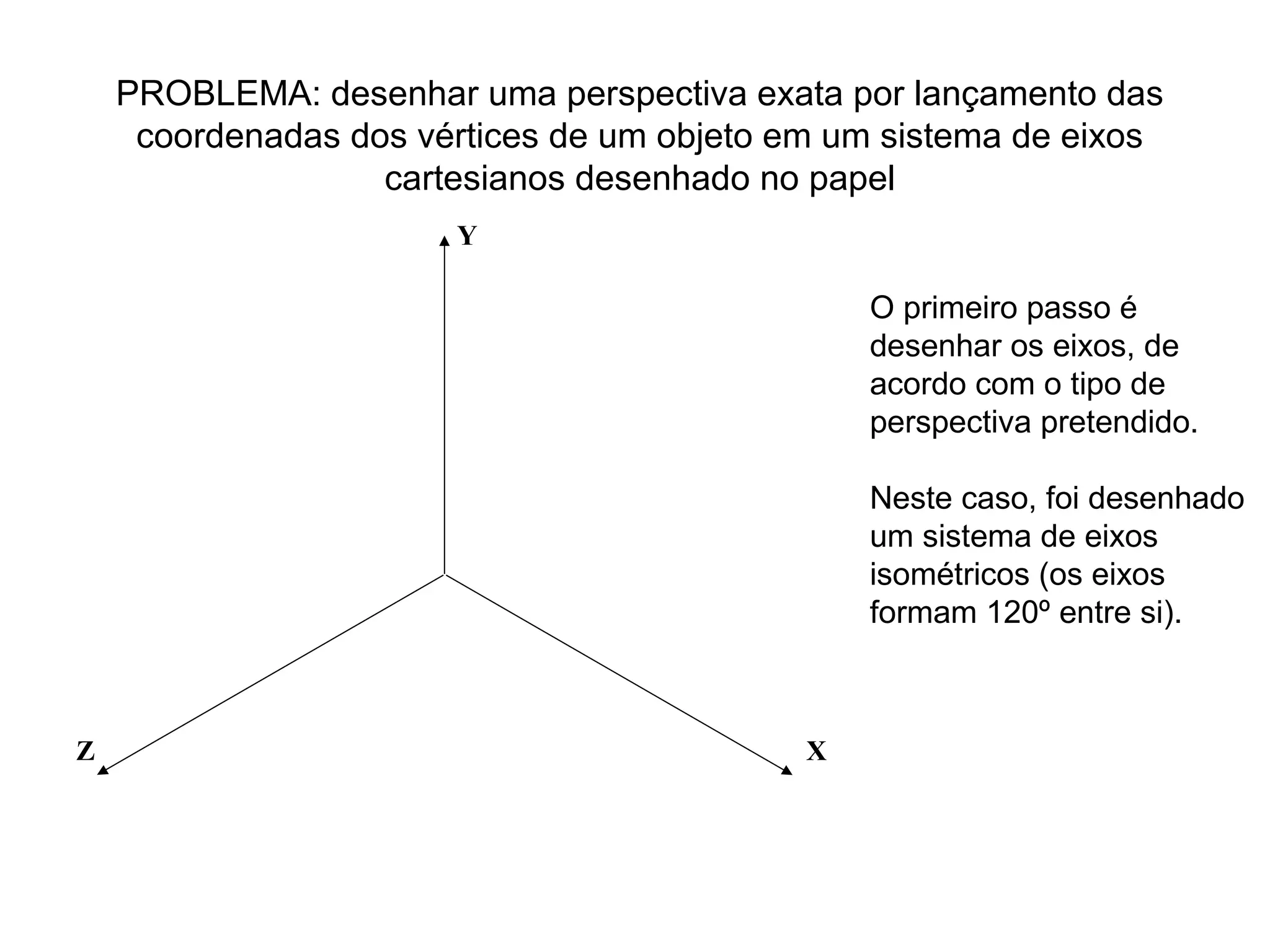
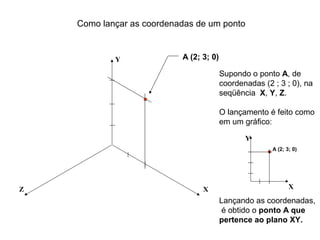
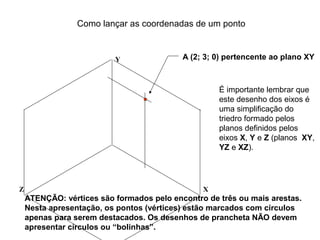
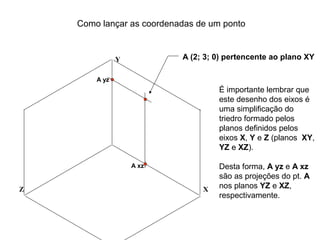
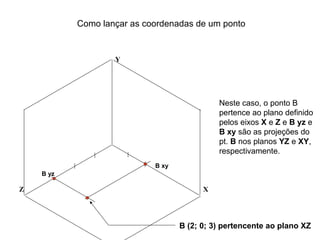
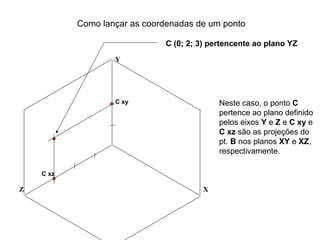
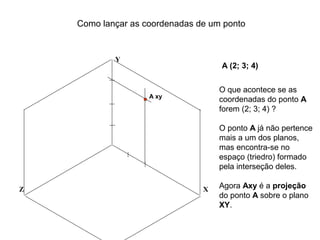
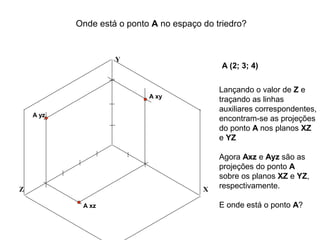
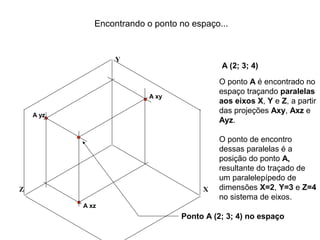
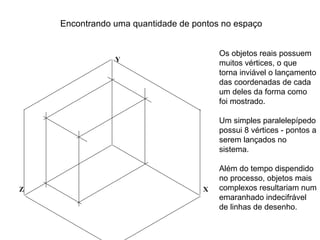
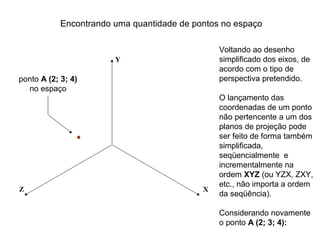
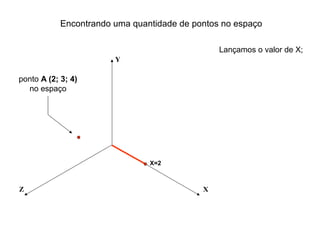
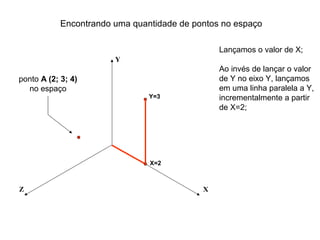
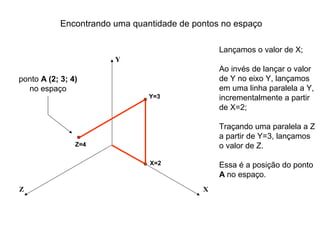
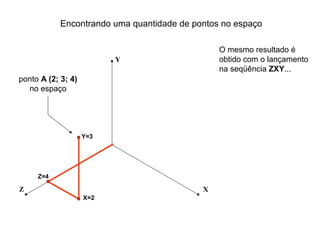
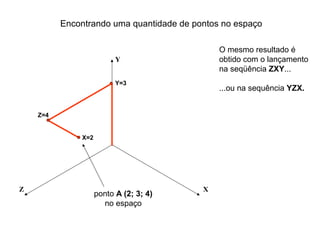
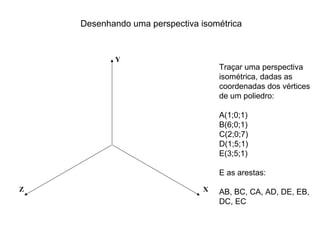
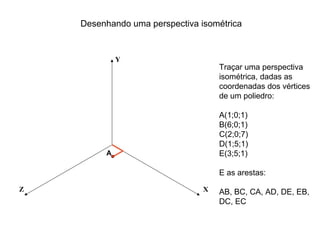
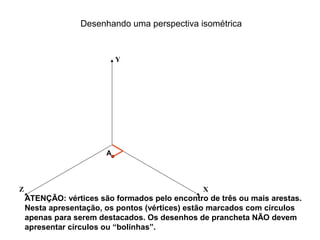
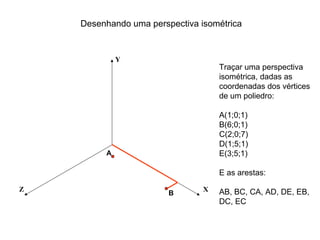
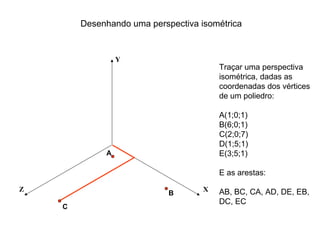
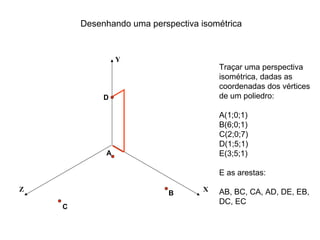
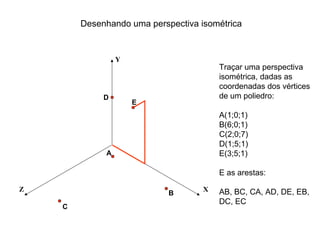
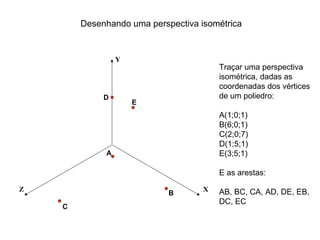
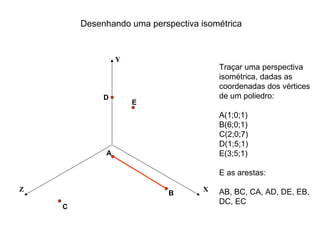
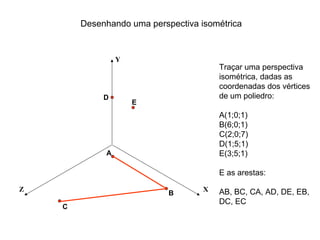
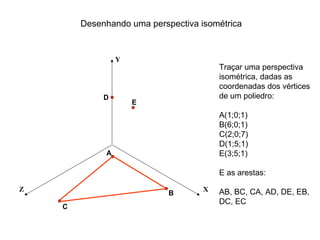
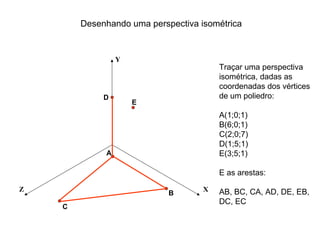
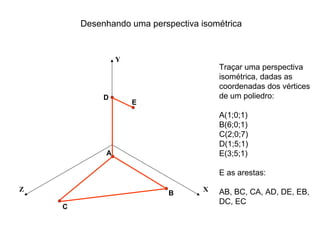
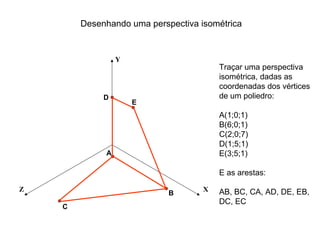
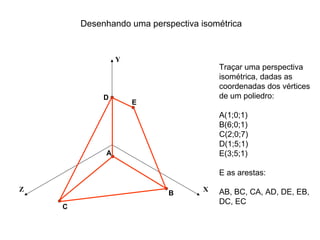
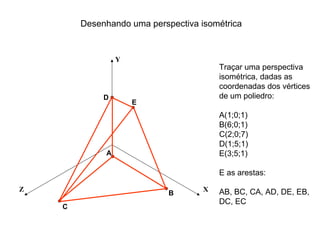
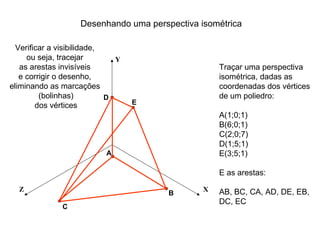
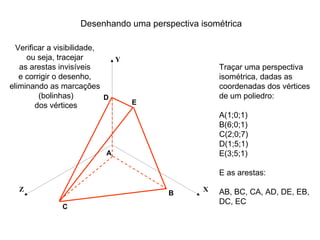
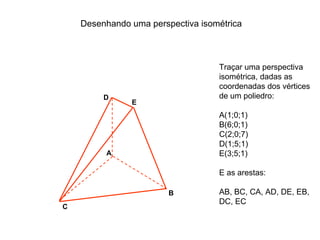
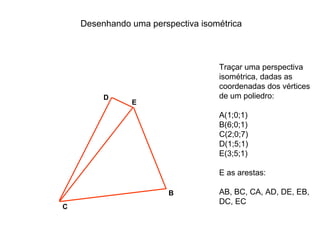
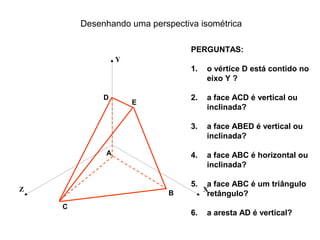
O documento explica como desenhar objetos em perspectiva lançando as coordenadas de seus vértices em um sistema de eixos cartesianos. Primeiro, os eixos são desenhados de acordo com o tipo de perspectiva. Em seguida, mostra como lançar as coordenadas de pontos pertencentes ou não a um plano de projeção, traçando linhas auxiliares entre as projeções do ponto nos diferentes planos até encontrar sua posição no espaço. Por fim, explica como lançar vários pontos de forma simplificada considerando a ordem sequencial XYZ.

1. PROBLEMA: desenhar uma perspectiva exata por lançamento das
coordenadas dos vértices de um objeto em um sistema de eixos
cartesianos desenhado no papel
Y
O primeiro passo é
desenhar os eixos, de
acordo com o tipo de
perspectiva pretendido.
Neste caso, foi desenhado
um sistema de eixos
isométricos (os eixos
formam 120º entre si).
Z X

2. Como lançar as coordenadas de um ponto
Y A (2; 3; 0)
Supondo o ponto A, de
coordenadas (2 ; 3 ; 0), na
seqüência X, Y, Z.
O lançamento é feito como
em um gráfico:
Y
A (2; 3; 0)
Z X X
Lançando as coordenadas,
é obtido o ponto A que
pertence ao plano XY.

3. Como lançar as coordenadas de um ponto
Y A (2; 3; 0) pertencente ao plano XY
É importante lembrar que
este desenho dos eixos é
uma simplificação do
triedro formado pelos
planos definidos pelos
eixos X, Y e Z (planos XY,
YZ e XZ).
Z X
ATENÇÃO: vértices são formados pelo encontro de três ou mais arestas.
Nesta apresentação, os pontos (vértices) estão marcados com círculos
apenas para serem destacados. Os desenhos de prancheta NÃO devem
apresentar círculos ou “bolinhas”.

4. Como lançar as coordenadas de um ponto
Y A (2; 3; 0) pertencente ao plano XY
A yz
É importante lembrar que
este desenho dos eixos é
uma simplificação do
triedro formado pelos
planos definidos pelos
eixos X, Y e Z (planos XY,
YZ e XZ).
A xz Desta forma, A yz e A xz
são as projeções do pt. A
Z X nos planos YZ e XZ,
respectivamente.

5. Como lançar as coordenadas de um ponto
Y
Neste caso, o ponto B
pertence ao plano definido
pelos eixos X e Z e B yz e
B xy são as projeções do
pt. B nos planos YZ e XY,
respectivamente.
B xy
B yz
Z X
B (2; 0; 3) pertencente ao plano XZ

6. Como lançar as coordenadas de um ponto
C (0; 2; 3) pertencente ao plano YZ
Y
C xy Neste caso, o ponto C
pertence ao plano definido
pelos eixos Y e Z e C xy e
C xz são as projeções do
pt. B nos planos XY e XZ,
respectivamente.
C xz
Z X

7. Como lançar as coordenadas de um ponto
Y
A (2; 3; 4)
O que acontece se as
A xy
coordenadas do ponto A
forem (2; 3; 4) ?
O ponto A já não pertence
mais a um dos planos,
mas encontra-se no
espaço (triedro) formado
pela interseção deles.
Z X Agora Axy é a projeção
do ponto A sobre o plano
XY.

8. Onde está o ponto A no espaço do triedro?
Y
A (2; 3; 4)
Lançando o valor de Z e
A xy
traçando as linhas
auxiliares correspondentes,
A yz
encontram-se as projeções
do ponto A nos planos XZ
e YZ
Agora Axz e Ayz são as
projeções do ponto A
sobre os planos XZ e YZ,
Z X respectivamente.
A xz E onde está o ponto A?

9. Encontrando o ponto no espaço...
Y
A (2; 3; 4)
O ponto A é encontrado no
espaço traçando paralelas
A xy
aos eixos X, Y e Z, a partir
das projeções Axy, Axz e
A yz
Ayz.
O ponto de encontro
dessas paralelas é a
posição do ponto A,
resultante do traçado de
um paralelepípedo de
Z X dimensões X=2, Y=3 e Z=4
no sistema de eixos.
A xz
Ponto A (2; 3; 4) no espaço

10. Encontrando uma quantidade de pontos no espaço
Os objetos reais possuem
Y
muitos vértices, o que
torna inviável o lançamento
das coordenadas de cada
um deles da forma como
foi mostrado.
Um simples paralelepípedo
possui 8 vértices - pontos a
serem lançados no
sistema.
Além do tempo dispendido
no processo, objetos mais
Z X complexos resultariam num
emaranhado indecifrável
de linhas de desenho.

11. Encontrando uma quantidade de pontos no espaço
Voltando ao desenho
Y simplificado dos eixos, de
acordo com o tipo de
ponto A (2; 3; 4) perspectiva pretendido.
no espaço
O lançamento das
coordenadas de um ponto
não pertencente a um dos
planos de projeção pode
ser feito de forma também
simplificada,
seqüencialmente e
incrementalmente na
ordem XYZ (ou YZX, ZXY,
etc., não importa a ordem
Z X
da seqüência).
Considerando novamente
o ponto A (2; 3; 4):

12. Encontrando uma quantidade de pontos no espaço
Lançamos o valor de X;
Y
ponto A (2; 3; 4)
no espaço
X=2
Z X

13. Encontrando uma quantidade de pontos no espaço
Lançamos o valor de X;
Y
Ao invés de lançar o valor
ponto A (2; 3; 4) de Y no eixo Y, lançamos
no espaço em uma linha paralela a Y,
Y=3 incrementalmente a partir
de X=2;
X=2
Z X

14. Encontrando uma quantidade de pontos no espaço
Lançamos o valor de X;
Y
Ao invés de lançar o valor
ponto A (2; 3; 4) de Y no eixo Y, lançamos
no espaço em uma linha paralela a Y,
Y=3 incrementalmente a partir
de X=2;
Traçando uma paralela a Z
a partir de Y=3, lançamos
Z=4 o valor de Z.
X=2 Essa é a posição do ponto
A no espaço.
Z X

15. Encontrando uma quantidade de pontos no espaço
O mesmo resultado é
Y obtido com o lançamento
na seqüência ZXY...
ponto A (2; 3; 4)
no espaço
Y=3
Z=4
Z X
X=2

16. Encontrando uma quantidade de pontos no espaço
O mesmo resultado é
Y obtido com o lançamento
na seqüência ZXY...
Y=3
...ou na sequência YZX.
Z=4
X=2
Z X
ponto A (2; 3; 4)
no espaço

17. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
de um poliedro:
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
DC, EC

18. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
de um poliedro:
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
DC, EC

19. Desenhando uma perspectiva isométrica
Y
A
Z X
ATENÇÃO: vértices são formados pelo encontro de três ou mais arestas.
Nesta apresentação, os pontos (vértices) estão marcados com círculos
apenas para serem destacados. Os desenhos de prancheta NÃO devem
apresentar círculos ou “bolinhas”.

20. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
de um poliedro:
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC

21. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
de um poliedro:
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

22. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

23. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

24. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

25. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

26. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

27. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

28. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

29. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

30. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

31. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

32. Desenhando uma perspectiva isométrica
Y
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

33. Desenhando uma perspectiva isométrica
Verificar a visibilidade,
ou seja, tracejar Y
as arestas invisíveis Traçar uma perspectiva
e corrigir o desenho, isométrica, dadas as
eliminando as marcações coordenadas dos vértices
(bolinhas) D de um poliedro:
dos vértices E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

34. Desenhando uma perspectiva isométrica
Verificar a visibilidade,
ou seja, tracejar Y
as arestas invisíveis Traçar uma perspectiva
e corrigir o desenho, isométrica, dadas as
eliminando as marcações coordenadas dos vértices
(bolinhas) D de um poliedro:
dos vértices E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
Z X AB, BC, CA, AD, DE, EB,
B
DC, EC
C

35. Desenhando uma perspectiva isométrica
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
A E(3;5;1)
E as arestas:
B AB, BC, CA, AD, DE, EB,
DC, EC
C

36. Desenhando uma perspectiva isométrica
Traçar uma perspectiva
isométrica, dadas as
coordenadas dos vértices
D de um poliedro:
E
A(1;0;1)
B(6;0;1)
C(2;0;7)
D(1;5;1)
E(3;5;1)
E as arestas:
B AB, BC, CA, AD, DE, EB,
DC, EC
C

37. Desenhando uma perspectiva isométrica
PERGUNTAS:
Y
1. o vértice D está contido no
eixo Y ?
D 2. a face ACD é vertical ou
E
inclinada?
3. a face ABED é vertical ou
inclinada?
A 4. a face ABC é horizontal ou
inclinada?
5. a face ABC é um triângulo
Z X
B retângulo?
C
6. a aresta AD é vertical?