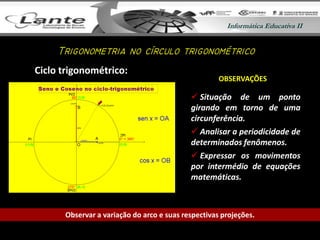
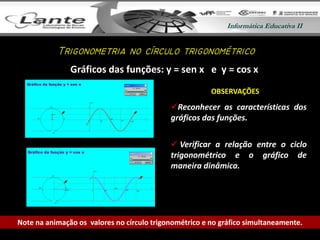
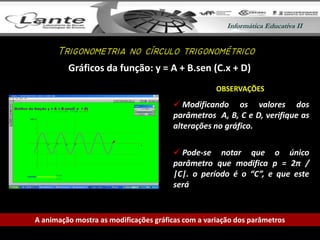
O documento apresenta uma aula sobre trigonometria no círculo trigonométrico. É feita uma revisão dos conceitos de graus, radianos e unidades de arco. Em seguida, são definidas e estudadas graficamente as funções seno, cosseno e tangente, relacionando-as ao círculo trigonométrico. Por fim, são apresentados os próximos tópicos a serem abordados.

1. Informática Educativa II
z

LANT-UFF

2. Informática Educativa II
Professor: Mário César Cunha

3. Informática Educativa IIInformática Educativa II

Observando os triângulos retângulos é possível perceber que as razões entre as medidas
de lados correspondentes de triângulos com um ângulo comum são congruentes
∆ABC ~ ∆ADE ~ ∆AXY
AY
XY
AE
DE
AC
BC
AY
AX
AE
AD
AC
AB
AX
XY
AD
DE
AB
BC
O que nos permite definir
O que nos permite definir
O que nos permite definir
hipotenusadamedida
aopostocatetodomedida
sen
hipotenusadamedida
aadjacentecatetodomedida
cos
aadjacentecatetodomedida
aopostocatetodomedida
tg
a
E

4. Informática Educativa IIInformática Educativa II
É importante destacar duas relações entre essas razões válidas para ângulo a
cos
sen
tg
1cos22
sen


5. Informática Educativa IIInformática Educativa II
Observe a periodicidade dos fenômenos naturais.
 Observe os contextos de aplicação.
 Note a necessidade das funções com periodicidade (repetição).
ATIVIDADES INICIAIS - MOTIVAÇÃO
Sb C 
T

6. Informática Educativa IIInformática Educativa II
GRAUS - medida angular do arco corresponde ao ângulo
central, medido em graus (1 grau = 1/360 do círculo).
RADIANOS - medida angular do arco coincide com a
medida do ângulo central em radianos (1 radiano é a
medida do ângulo cujo arco tem o mesmo comprimento
que o raio do círculo).
UNIDADES DOS ARCOS
T

7. Informática Educativa IIInformática Educativa II
Ciclo trigonométrico:
 Situação de um ponto
girando em torno de uma
circunferência.
 Analisar a periodicidade de
determinados fenômenos.
 Expressar os movimentos
por intermédio de equações
matemáticas.
Observar a variação do arco e suas respectivas projeções.
OBSERVAÇÕES
T

8. Informática Educativa IIInformática Educativa II
Funções seno e co-seno
Definição: Função seno
seno
co-seno
Perceber a definição das funções como as projeções do arco sobre os eixos.
a
a
O
P2
O P1
sen : R  R
a sen a = OP2
cos : R  R
a cos a = OP1
Definição: Função co-seno
T

9. Informática Educativa IIInformática Educativa II
Gráficos das funções: y = sen x e y = cos x
Reconhecer as características dos
gráficos das funções.
 Verificar a relação entre o ciclo
trigonométrico e o gráfico de
maneira dinâmica.
Note na animação os valores no círculo trigonométrico e no gráfico simultaneamente.
OBSERVAÇÕES
T

10. Informática Educativa IIInformática Educativa II
Gráficos da função: y = A + B.sen (C.x + D)
 Modificando os valores dos
parâmetros A, B, C e D, verifique as
alterações no gráfico.
 Pode-se notar que o único
parâmetro que modifica p = 2π /
|C|. o período é o “C”, e que este
será
A animação mostra as modificações gráficas com a variação dos parâmetros
OBSERVAÇÕES
T

11. Informática Educativa IIInformática Educativa II
 Definição de função tangente
 Estudo das equações e inequações trigonométricas.
 Relações entre as funções.
Próximos assuntos:
Fazer os exercícios propostos para o trabalho extra classe
T

12. Informática Educativa IIInformática Educativa II
b
A
T