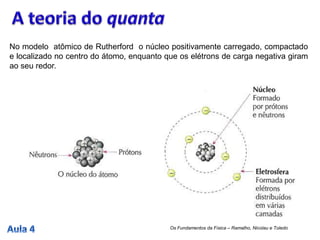
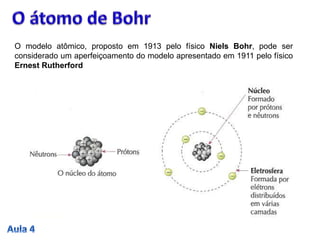
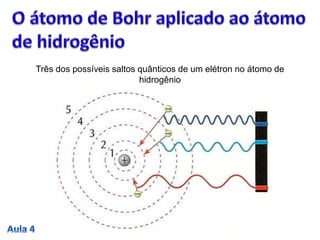
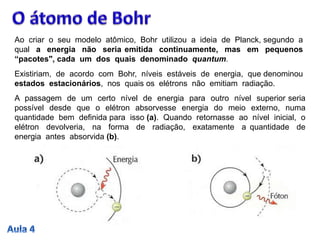
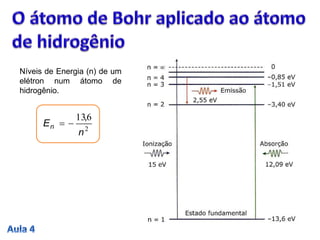
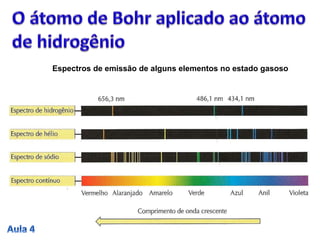
1. O modelo atômico de Rutherford propôs que o átomo possui um núcleo positivamente carregado no centro, com elétrons girando em órbitas ao seu redor 2. O modelo de Bohr aperfeiçoou o modelo de Rutherford, propondo que os elétrons descrevem órbitas circulares estáveis em torno do núcleo, chamadas de estados estacionários 3. A passagem do elétron entre estados estacionários envolve a absorção ou emissão de quanta de energia definidos pela const

3. No modelo atômico de Rutherford o núcleo positivamente carregado, compactado
e localizado no centro do átomo, enquanto que os elétrons de carga negativa giram
ao seu redor.
Os Fundamentos da Física – Ramalho, Nicolau e Toledo

4. Embora o modelo de Rutherford explicasse satisfatoriamente a maior parte
dos fenômenos físicos e químicos, havia um problema que não podia ser
explicado. Como se sabe, corpos em órbitas apresentam aceleração
centrípeta. Entretanto, conforme preconiza a teoria de Maxwell, cargas
aceleradas irradiam energia. Então, os elétrons estariam continuamente
emitindo radiações e, em consequência dessa perda energética, deveriam
"cair" no núcleo, acarretando um colapso da matéria.

5. Cada átomo (oscilador) só pode absorver ou emitir radiação de uma determinada
frequência natural.
Um elétron, oscilando com frequência f, emite (ou absorve) uma onda eletromagnética
de igual frequência, porém a energia não é emitida (ou absorvida) continuamente.
Plank considerou que a energia radiante não é emitida (ou absorvida) de modo
contínuo, mas sim em porções descontínuas, “partículas” que transportam, cada qual,
uma quantidade de energia E bem definida. Essas “partículas” de energia foram
denominadas fótons.
O quantum E de energia radiante de frequência f é dado por:
fhE 
h = 6,63 x 10–34 J.s é a constante de Plank

6. Ou o elétron absorve (ou emite)
um quantum (E = h.f) ou nada
O quantum (no plural quanta) é a energia E de
cada fóton
Planck

7. Bohr faz a sua aparição! Bohr, físico
dinamarquês, tinha 26. Ele também foi estava
realizando pesquisas sobre o átomo no mesmo
laboratório onde Rutherford tinha estudado.
Bohr fez importantes contribuições para a
descrição do mundo invisível, e para o pleno
desenvolvimento da mecânica quântica. Não
podemos falar da mecânica quântica sem
mencioná-lo

8. O modelo atômico, proposto em 1913 pelo físico Niels Bohr, pode ser
considerado um aperfeiçoamento do modelo apresentado em 1911 pelo físico
Ernest Rutherford

9. Ao criar o seu modelo atômico, Bohr utilizou a ideia de Planck, segundo a
qual a energia não seria emitida continuamente, mas em pequenos
“pacotes", cada um dos quais denominado quantum.
Existiriam, de acordo com Bohr, níveis estáveis de energia, que denominou
estados estacionários, nos quais os elétrons não emitiam radiação.
A passagem de um certo nível de energia para outro nível superior seria
possível desde que o elétron absorvesse energia do meio externo, numa
quantidade bem definida para isso (a). Quando retornasse ao nível inicial, o
elétron devolveria, na forma de radiação, exatamente a quantidade de
energia antes absorvida (b).

10. 1. O elétron descreve órbitas circulares em torno do núcleo.
2. Apenas algumas órbitas estáveis, bem definidas, denominadas estados
estacionários, são permitidas ao elétron
3. A passagem do elétron de um estado estacionário para outro é
possível mediante a absorção ou liberação de energia pelo átomo
Ao passar de um estado estacionário, de energia E, para outro, de
energia E' (com E' > E), teremos:
fhEE '
Assim, sendo m a massa do elétron, v a velocidade orbital e r o raio da
órbita descrita, teremos:
4. As órbitas permitidas ao elétron são aquelas em que o momento
angular orbital do elétron é um múltiplo inteiro de , onde
2
h

 nrvm (com n = 1, 2, 3, 4, ...)

11. Com base nesses quatro postulados, Bohr pôde calcular os raios das
órbitas permitidas e suas respectivas energias, bem como os comprimentos
de onda associados, para o átomo de hidrogênio. O estado estacionário
fundamental corresponde ao de menor raio, denominado raio de Bohr.
Para ele, n = 1.
2
0 eKm
rB



Sendo: m = 9,1 ∙ 10–31 kg; K0 = 9 ∙ 109 N∙m2/C2; e = 1,6 ∙ 10–19 C
530,Br Å

12. Para os demais estados
permitidos, os raios
podem ser obtidos em
função do raio de Bohr
pela fórmula:
Bn rnr  2
Bn rnr  2
n = 1, 2, 3, ...

13. 2
613
n
En
,









 2
2
0 1
2 nr
eK
E
B
n
Substituindo os valores das constantes K0, e e rB, obtém-se para essa
energia, expressa em elétron-volt (eV):
A energia mecânica total En do elétron no enésimo estado estacionário é
dada pela soma das energias cinética e potencial:

14. 2
613
n
En
,

Níveis de Energia (n) de um
elétron num átomo de
hidrogênio.

15. Espectros de emissão de alguns elementos no estado gasoso

16. Três dos possíveis saltos quânticos de um elétron no átomo de
hidrogênio

17. O modelo atômico de Bohr funcionava muito bem para o átomo
de hidrogênio. Porém, ao realizar medidas dos espectros para
átomos de outros elementos, observou-se que muitas das linhas
da série de Balmer, juntamente com outras, não eram linhas
únicas, mostrando que algo estava errado em seu modelo.
Em 1916, W. Wilson e A. Sommerfeld sugeriu que as órbitas
eletrônicas podem ser elípticas, com o núcleo em um dos focos
da elipse. Nesse contexto se quantifica a orientação das órbitas
no espaço e admitem mudanças relativísticas da massa do
elétron quando viaja a altas velocidades ao redor do núcleo.

18. Quando Bohr propôs se modelo atômico achou o valor de RH = 109,737 cm-1,
enquanto o valor experimental de Rydberg era RH = 109,677581 cm-1 (em
grande escalar não parece muito, porém a nível espectrais é demasiadamente
diferente).
Sommerfeld sugeriu que a massa m do elétron deve ser representada pela
massa m do sistema, formada pela massa do núcleo M e a massa do elétron m.
Mm
Mm


m

19. A constante de Rydberg pode ser escrita em função da massa do elétron:
ch8
meZ
R
32
0
42


Então, para a massa reduzida:
ch8
eZ
R
32
0
42

m

E com base nessa equação calculou a constate de Rydberg:
1
H cm677560,109R 


20. Problemas:
 O modelo atômico de Bohr, só é válido para o átomo de hidrogênio, não
sendo capaz de explicar os espectros de emissão de átomos
polielectrônicos.
 Por volta de 1916 o espectrômetros permitiram abservar as raias, antes
consideradas simples, são na verdade duas muito juntas. Isso supõe saltos
de elétrons a estados energéticos muito próximos.
Portanto:
 Nos níveis de energia definidos no modelo de Bohr, devemos considerar a
existência de subníveis de energia.
 Para um determinado nível de energia, o elétron pode estar se movendo em
órbitas circulares, ou elípticas.
Solução:
 Um segundo número quântico (l) que define os diferentes subníveis de
energia ou, diferentes tipos de órbitas em que o elétron pode se mover.
Ver

21. Os valores que podem tomar o
número quântico secundário
(l) para um dado valor de n,
que varia de 0 até o valor de
(n-1)
Os vários subníveis de energia
possíveis, definidos pelos
valores de "l", da seguinte
forma:
Subnível "s" quando l = 0
Subnível "p" quando l = 1
Subnível "d" quando l = 2
Subnível "f" quando l = 3
21
Disponívelem:http://pt.slideshare.net/RebecaVale/7-nveis-de-energia

22. Porque:
 Quando os espectros de emissão atômica são obtidos na vizinhança de um campo
magnético intenso, observa-se desdobramento nas linhas espectrais.
Portanto:
 Esta separação é associada a diferentes orientações para fazer órbitas elípticas na
presença de um campo magnético.
Solução:
 Um terceiro número quântico (m), chamado número quântico magnético, que
define as novas possibilidades encontradas para os elétrons, que pode assumir os
seguintes valores: - l passando por 0 até + l
22

23. 23

24. Porque:
 O modelo atômico de Bohr, incluindo mudanças na Sommerfeld e Zeeman,
não poderia explicar algumas propriedades dos espectros atômicos.
Portanto:
 A possibilidade de que o elétron pode girar sobre si mesmo com um dado
valor de momento angular. Existem dois possíveis movimentos de rotação, que
dão uma explicação mais completa aos espectros atômicos é sugerido.
Solução:
 Um quarto número quântico (s), número
chamado spin, que define o sentido de
rotação e pode assumir apenas dois valores:
+½ ou -½.

25. Atividade 04
a) Resolver os exercícios propostos da aula 04;
b) Assistir ao vídeo:
https://www.youtube.com/watch?v=LNkOPbE5aNU

26. - CARUSO, Francisco e OGURI, Vitor. Física Moderna, Origens Clássicas e Fundamentos Quânticos. Rio de
Janeiro: Ed. Campus, 2006.
- MARTINS, Jader B. A História do Átomo, de Demócrito aos Quarks. Rio de Janeiro: Editora Ciência Moderna,
2001
- PERUZZO, Francisco M. e CANTO, Eduardo L. Química da Abordagem do Cotidiano. Vol. 1, 4ª Ed. São Paulo:
Editora Moderna, 2006.
- RAMALHO, Francisco J., JUNIOR, Nicolau G. F. e SOARES, Paulo A. T. Fundamentos da Física. Vol 3, 9ª Ed. São
Paulo: Editora Moderna, 2008.
- SEGRÈ, Emilio. Dos Raios X aos Quarks – Físicos Modernos e Suas Descobertas. Brasília: Editora
Universidade de Brasília, 1987.
- TRANSNATIONAL COLLEGE OF LEX. What Is Quantum Mechanics? A Physics Adventure. Boston, 1996.
Disponível em <http://www.trabalhosfeitos.com/ensaios/Atomismo-e-S%C3%B3crates/39657490.html> Acesso em
Julho de 2015.
Disponível em <http://www.fullquimica.com/2011/03/teoria-atomica-y-modelos-atomicos.html> Acesso em Julho de
2015.
Disponível em <https://viveraciencia.wordpress.com/2009/06/09/atomo-poesia-memoria-um-lucrecio-perdido-no-livro-
de-quimica/> Acesso em Julho de 2015.
Disponível em <http://pt.slideshare.net/RebecaVale/7-nveis-de-energia> Acesso em Julho de 2015.