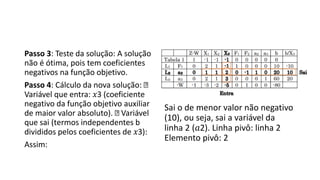
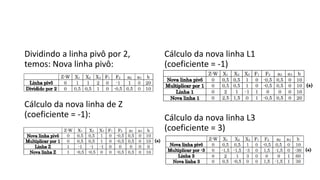
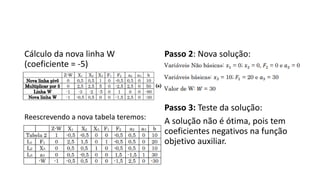
O documento descreve as variações no método simplex para lidar com diferentes tipos de restrições e funções objetivo, como: (1) adicionar variáveis auxiliares para restrições do tipo igualdade ou maior que; e (2) multiplicar a função objetivo por -1 para problemas de minimização. O método das duas fases é introduzido para resolver esses problemas, minimizando as variáveis auxiliares na primeira fase antes de resolver o problema original na segunda fase. Casos especiais como degeneração e soluções ótimas alternativas também são discutidos.

1. Pesquisa Operacional – Aula 07
Solução pelo Método Simplex

2. Variação das aplicações do Método Simplex
Nos exemplos que foram resolvidos em aulas anteriores, vamos trabalhar com o
método tabular Simplex.
As restrições eram todas do tipo ≤ com os termos da direita positivos.
O acréscimo das variáveis de folga fornece nesse caso uma solução básica inicial.
Veremos agora os demais tipos:
1. A restrição é do tipo ≥: a variável de folga tem valor negativo, quando se
anulam as variáveis de decisão.
2. A restrição é do tipo =: não receba a variável de folga.
Quando estes tipos de restrições ocorrem, acrescentamos variáveis auxiliares 𝑎𝑖
com formação de um novo modelo. A solução básica inicial do novo modelo é
formada pelas variáveis de folga das restrições do tipo ≤ e pelas variáveis auxiliares
𝑎𝑖 .

3. Exemplo
Como descrito anteriormente, o termo −𝐹2
foi adicionado, uma vez que a restrição é do
tipo ≥.
Entretanto, nessas condições não há
solução básica inicial, devidos às restrições
2 e 3.
Observe que, pela restrição 2: 𝐹2 = −20,
que não pode ser uma solução inicial
devido ao princípio da não negatividade (𝐹2
≥ 0).
Já na restrição 3 não existe variável para
fazer parte da solução básica inicial, o que
resultaria em 0 = 60, que é
matematicamente falso. Por conta disso,
deverá haver uma etapa adicional dentro
do passo 1.

4. Acrescentar variáveis auxiliares
(também chamadas de variáveis
artificiais) na segunda e na terceira
restrição:
A partir daí temos uma solução
básica inicial: 𝐹1 = 10, 𝑎2 = 20 e 𝑎3 =
60 com todas as outras variáveis
nulas.
Além dessa variação nas restrições,
existe também a possibilidade de a
função objetivo ser de minimização.
Nesse caso, deve-se multiplicar a
função objetivo por -1.
Assim, obtém-se uma função
equivalente para a maximização.

5. Além dessa variação nas
restrições, existe também a
possibilidade de a função objetivo
ser de minimização.
Nesse caso, deve-se multiplicar a
função objetivo por -1.
Assim, obtém-se uma função
equivalente para a maximização.
• Exemplo:
O modelo equivalente será então:

6. • Então: Resolvido o modelo equivalente,
teremos a solução do modelo original
com a troca do sinal de Z.
Por exemplo, a solução desse problema
é 𝑥1 = 0, 𝑥2 = 15 e 𝑥3 = 5,
o que resulta em 𝑍 = 55.
Contudo, na minimização temos que
fazer −Z = −55.
Logo, a solução desse problema de
minimização é
𝑥1 = 0, 𝑥2 = 15 e 𝑥3 = 5,
que resulta em 𝑍 = −55.

7. O método das duas fases:
Esse método foi desenvolvido para
atender a equações e inequações dos
tipos = e ≥, nas quais são acrescentadas
as variáveis auxiliares (ou artificiais).
O objetivo é, em uma primeira fase,
minimizar a soma das variáveis
artificiais até obter o valor de zero.
Ao final da primeira fase chega-se a um
problema que pode ser resolvido pelo
método Simplex convencional (na
segunda fase).
Começaremos a estudar esse método
construindo uma função objetivo
auxiliar (ou artificial) 𝑊, formada pela
soma das variáveis auxiliares:
A função 𝑊 deve ser escrita em termos
das variáveis originais na forma de uma
função objetivo de minimização.
O objetivo é minimizar 𝑊, pois as
variáveis auxiliares devem ser iguais a
zero (para evitar inconsistências
matemáticas).

8. Quando as variáveis auxiliares forem
não básicas, então:
Logo:
Quando isso ocorrer a fase 1 estará
terminada e haverá uma nova função
objetivo 𝑍 a ser resolvida (fase 2) via
método Simplex convencional (ou
seja, teremos um modelo original
com solução básica inicial, dando
início aos cálculos para se chegar na
solução ótima).
Exemplo:

9. Passo 1: Adicionamos as variáveis
de folga e as variáveis auxiliares
(como foi feito anteriormente):
Definimos a função objetivo
auxiliar:
Isolando 𝑎2 na segunda restrição
e isolando 𝑎3 na restrição 3:

10. Logo: O quadro com a função auxiliar fica:

11. Passo 3: Teste da solução: A solução
não é ótima, pois tem coeficientes
negativos na função objetivo.
Passo 4: Cálculo da nova solução:
Variável que entra: 𝑥3 (coeficiente
negativo da função objetivo auxiliar
de maior valor absoluto). Variável
que sai (termos independentes b
divididos pelos coeficientes de 𝑥3):
Assim:
Sai o de menor valor não negativo
(10), ou seja, sai a variável da
linha 2 (𝑎2). Linha pivô: linha 2
Elemento pivô: 2

12. Dividindo a linha pivô por 2,
temos: Nova linha pivô:
Cálculo da nova linha de Z
(coeficiente = -1):
Cálculo da nova linha L1
(coeficiente = -1)
Cálculo da nova linha L3
(coeficiente = 3)

13. Cálculo da nova linha W
(coeficiente = -5)
Reescrevendo a nova tabela teremos:
Passo 2: Nova solução:
Passo 3: Teste da solução:
A solução não é ótima, pois tem
coeficientes negativos na função
objetivo auxiliar.

14. Passo 4: Cálculo da nova solução:
• Variável que entra: 𝐹2
(coeficiente -1,5).
• Variável que sai (termos
independentes b divididos pelos
coeficientes de 𝐹2):
Assim:
Sai o de menor valor não negativo (20),
ou seja, sai a variável da linha 3 (𝑎3).
Linha pivô: linha 3 Elemento pivô: 1,5
Dividindo a linha pivô por 1,5, temos:
Nova linha pivô:

15. Cálculo da nova linha de Z (coeficiente = -0,5):
Cálculo da nova linha L1 (coeficiente = -0,5):
Cálculo da nova linha L2 (coeficiente = -0,5):
Cálculo da nova linha W (coeficiente = -1,5):
Nova tabela:

16. Passo 2: Nova solução:
Passo 3: Teste da solução: o problema apresenta
agora uma solução básica formada pelas
variáveis originais (observe que tanto as
variáveis auxiliares 𝑎2 e 𝑎3 quanto a função
objetivo auxiliar 𝑊 são nulas). Isso significa que
a Fase 1 do método das duas fases foi concluída.
Nesse ponto devemos abandonar as variáveis
auxiliares (𝑎2 e 𝑎3) e a função objetivo auxiliar
(𝑊). Iniciamos a Fase 2, buscando a solução do
problema com a função objetivo original em Z.
A tabela 1 da Fase 2 se torna, portanto:
A partir dessa tabela, damos sequência ao
método Simplex para obter a solução ótima de
𝑍 (da forma como aprendemos na seção
anterior).

17. Para este problema em particular, após aplicar
todas as etapas do método Simplex chegaremos
a seguinte solução:
Assim, a solução ótima é 𝑍 = 35 e ocorre
quando 𝑥1 = 0, 𝑥2 = 22,5 e 𝑥3 = 12,5.
Vale ressaltar que, caso a função auxiliar 𝑊
apresente solução ótima com valor não nulo, as
variáveis auxiliares não serão todas nulas.
Nesse caso, o modelo original não possuirá uma
solução básica, e portanto o problema é dito
“sem solução”.
Em outras palavras, se a solução ótima de 𝑊 for
diferente de zero, o problema não tem solução
viável (ou seja, o problema não possui solução
que satisfaça todas as restrições; quando isso
ocorre dizemos que as restrições “não são
consistentes”).

18. Casos especiais do Método Simplex
Serão considerados quatro casos
especiais que podem surgir na
utilização do método Simplex:
1. Degeneração;
2. Soluções ótimas alternativas
(também denominada
“múltiplas soluções ótimas”);
3. Soluções ilimitadas;
4. Soluções não existentes (ou
“soluções inviáveis”).
Existem dois motivos para se
estudar esses casos especiais:
1. Apresentar uma explicação
teórica para essas situações;
2. Dar uma interpretação prática
do significado desses
resultados em problemas
reais.

19. Degeneração
Na aplicação da condição de viabilidade (“sai da base a menor razão
não negativa”) pode ocorrer um empate na razão mínima entre duas
ou mais variáveis (nesse caso, podemos escolher a variável que sai de
forma arbitraria).
Quando isso acontece, no mínimo uma variável básica será zero na
iteração seguinte, e diz-se que a nova solução é degenerada (ou seja,
pelo menos uma variável básica é igual a zero).
Imagine que duas linhas tenham a mesma razão. Nesse caso, a linha
não escolhida terá o seu valor de 𝑏 = 0 (e consequentemente, a variável
básica associada a ela será igual a 0).

20. Soluções ótimas alternativas
Quando a função objetivo tem direção paralela a uma restrição
vinculadora (também chamada de restrição vinculante), ou seja, uma
restrição não redundante (restrição que é satisfeita como uma equação
na solução ótima; ou, graficamente, restrição que tangencia a área das
soluções viáveis), a função objetivo pode assumir o mesmo valor ótimo
em mais de um ponto de solução (isto é, o valor ótimo ocorre para
qualquer ponto ao longo dessa “reta tangente” à área das soluções
viáveis).
Nesse caso, o problema possui soluções ótimas alternativas (ou
múltiplas soluções ótimas).

21. Soluções ótimas alternativas
No método Simplex, se o coeficiente de uma variável 𝑥𝑖 não básica (na
função objetivo) é zero, 𝑥𝑖 pode entrar na solução básica sem alterar o
valor de 𝑍, mas causando uma mudança nos valores das outras
variáveis.
É importante ressaltar que o método Simplex apenas determina os dois
“pontos de quina” (ou “pontos críticos” ou “pontos extremos”).
Matematicamente, para determinar os demais pontos basta fazer uma
média ponderada entre esses dois pontos. Na prática soluções ótimas
alternativas são úteis pois permitem a escolha entre muitas soluções
sem que o valor da função objetivo sofra deterioração.

22. Solução ilimitada
Em alguns problemas de PL, os valores das variáveis podem ser
aumentados indefinidamente sem violar nenhuma das restrições.
Nesse caso, a região das soluções é ilimitada em, no mínimo, uma das
variáveis de decisão (ao menos uma das variáveis de decisão tem valor
“infinito”).
O resultado é que o valor da função objetivo pode crescer (para o caso
da maximização) ou decrescer (para o caso da minimização)
indefinidamente (para “infinito”).
Nesse caso, a região das soluções, bem como o valor ótimo da função
objetivo, são ilimitados.

23. Solução ilimitada
No método Simplex, essa situação ocorre quando nenhuma variável se
qualifica para ser a variável básica que sai (ou seja, a condição de
viabilidade não é satisfeita).
Isso ocorre quando todos os coeficientes da coluna pivô (sem contar
com a linha da função objetivo) são negativos ou igual a zero (fazendo
com que a razão seja sempre negativa ou “infinita” para todas as
restrições).
Se a variável que entra é negativa ou zero, ela pode ser aumentada
indefinidamente (sem tornar as variáveis básicas atuais negativas).

24. Solução ilimitada
Na prática, a falta de limites indica a possibilidade de o modelo ter sido
mal construído.
A irregularidade mais provável é que uma ou mais restrições não
redundantes deixaram de ser levadas em conta e/ou os parâmetros (as
constantes) de algumas das restrições podem não ter sido estimados
corretamente.

25. Solução inviável
Problemas de PL que possuam restrições inconsistentes podem não ter
nenhuma solução viável.
Graficamente, não haverá uma região das soluções viáveis se não
houver uma área formada pela interseção entre as áreas das restrições.
É importante observar que se todas as restrições forem do tipo ≤ com
constantes do lado direito não negativas então certamente haverá uma
região viável (pois as folgas irão fornecer uma solução viável).

26. Solução inviável
Para outros tipos de restrições, utilizamos as variáveis artificiais.
Embora as variáveis artificiais sejam “punidas” na função objetivo para
força-las a zero na solução ótima, isso só irá acontecer se o modelo
tiver uma região viável.
Caso contrário, ao menos uma variável artificial será positiva na
iteração ótima (quando isso ocorre, certamente o problema não terá
solução viável).
Do ponto de vista prático, a não existência de uma região viável indica a
possibilidade de o problema não ter sido formulado corretamente.

27. Dualidade
O modelo inicial (ou “original”) de um problema
de programação linear, chamado de Primal,
pode ser substituído por um outro modelo que
chamamos de Dual.
Isso será possível em determinadas situações
nas quais a quantidade de cálculos necessária
para solucionar um modelo linear pelo método
Simplex pode ser reduzida.
Considere o modelo de programações linear
que tem a função objetivo de maximização, as
restrições são do tipo ≤ e as variáveis são não
negativas.
Chamamos esse modelo de Primal ao qual
podemos associar outro modelo que chamamos
de Dual, que será construído da seguinte
maneira:
1. Variáveis de decisão do dual: para cada
restrição do primal, criaremos uma variável
de decisão 𝑦𝑖 correspondente no dual.
2. Função objetivo no dual: a função objetivo
será de minimização. Cada um dos termos
na função objetivo consiste no produto da
variável 𝑦𝑖 pelo termo da direita da
restrição correspondente. Em outras
palavras, as constantes 𝑏 do lado direito
das restrições no primal se tornam os
coeficientes das variáveis de decisão 𝑦𝑖 na
função objetivo do dual.

28. Dualidade
3. Restrições: cada variável de decisão 𝑥𝑖
no primal gera uma restrição no dual.
4. Termos da esquerda das restrições no
dual: cada termo é o produto da
variável de decisão 𝑦𝑖 pelo coeficiente
respectivo da variável de decisão da
restrição 𝑖 no primal. Ou seja, os
coeficientes da primeira restrição serão
os coeficientes de 𝑦1...
5. Sinal: os sinais ≤ serão substituídos por
sinais de ≥ nas restrições.
6. Termos da direita: são os coeficientes
da variável 𝑥𝑖 na função objetivo
primal.
Nesse momento, é importante observar
que o Dual, de certa forma, é uma espécie
de “matriz transposta” do Primal (as linhas
se tornam colunas).
Exemplo: Primal:

29. Dualidade
Dual:
Observe que:
1. Como são três restrições no
primal foram criadas três
variáveis de decisão no dual.
2. Como a função objetivo no
primal era de maximização (Max
𝑍), no dual a função objetivo é
de minimização (Min 𝐷). Além
disso, os coeficientes da função
objetivo no dual são as
constantes 𝑏 do primal (10, 20 e
30).
3. Como são três variáveis de
decisão no primal foram criadas
três restrições no dual.

30. Dualidade
4) Os coeficientes da restrição 1 no primal
são os coeficientes de 𝑦1 no Dual; os
coeficientes da restrição 2 no primal
são os coeficientes de 𝑦2 no Dual e os
coeficientes da restrição 3 no primal
são os coeficientes de 𝑦3 no Dual.
5) Os sinais ≤ das restrições do primal
geram sinais ≥ nas variáveis do dual
(sinais inversos), enquanto os sinais ≥
das variáveis do primal geram sinais ≥
nas restrições do dual (mesmo sinal).
6) As constantes da direita nas restrições
são os coeficientes da função objetivo
(2, 3 e 1).
Note que foi feita uma operação parecida
com a de uma matriz transposta. Considere
uma matriz correspondente ao modelo
Primal escrita na seguinte forma:
Observe que a primeira linha apresenta os
coeficientes da função objetivo, a primeira
coluna (a partir da segunda linha) apresenta
as constantes do lado direito das restrições,
e os demais termos são os coeficientes do
lado esquerdo de cada restrição.

31. Dualidade
Na transposta, transformamos linhas em
colunas (a linha 1 se torna a coluna 1, a
linha 2 se torna a coluna 2...), assim:
Como na matriz 𝑀 (matriz dos termos da
primal), na matriz 𝑀𝑡 (dos termos da dual)
a primeira linha apresenta os coeficientes
da função objetivo, a primeira coluna (a
partir da segunda linha) apresenta as
constantes do lado direito das restrições, e
os demais termos são os coeficientes do
lado esquerdo de cada restrição.
De forma análoga, considere o seguinte
modelo Primal:
1. Função objetivo de minimização.
2. Restrições do tipo ≥.
3. Variáveis todas não negativas.
Nesse caso, seu Dual será:
1. Função objetivo de maximização.
2. Restrições do tipo ≤.
3. Variáveis todas não negativas.

32. Dualidade
Como exemplo, vamos considerar
o modelo Dual (do exemplo
anterior) como sendo o Primal
agora.
Exemplo:
Primal:
Dual:
Note que o resultado é o Primal
do primeiro exemplo. Logo, “o
Dual de um Dual é o modelo
Primal”.

33. Dualidade
Observe que:
1. Como são três restrições no primal
foram criadas três variáveis de decisão
no dual.
2. Como a função objetivo no primal era
de minimização (Min 𝑍), no dual a
função objetivo é de maximização (Max
𝐷). Além disso, os coeficientes da
função objetivo no dual são as
constantes 𝑏 do primal (2, 3 e 1).
3. Como são três variáveis de decisão no
primal foram criadas três restrições no
dual.
4. Os coeficientes da restrição 1 no primal
são os coeficientes de 𝑦1 no Dual; os
coeficientes da restrição 2 no primal
são os coeficientes de 𝑦2 no Dual e os
coeficientes da restrição 3 no primal
são os coeficientes de 𝑦3 no Dual.
5. Os sinais ≥ das restrições do primal
geram sinais ≥ nas variáveis do dual
(mesmo sinal), enquanto os sinais ≥
das variáveis do primal geram sinais ≤
nas restrições do dual (sinais inversos).
6. As constantes da direita nas restrições
são os coeficientes da função objetivo
(10, 20 e 30).

34. Dualidade
Observações adicionais:
• Se uma restrição primal é do tipo =, a variável
dual correspondente será sem restrição de
sinal (irrestrita em sinal).
• Se uma variável primal for sem restrição de
sinal, as restrições do dual correspondente
será do tipo =.
Exemplo:
Primal:
Dual:

35. Dualidade
Podemos resumir essas regras na seguinte tabela:
Observe que a tabela não utiliza a notação primal e dual. O que importa aqui é o sentido da
otimização (se o primal for de maximização, então o dual será de minimização e vice-versa).

36. Propriedades importantes do Primal-Dual
As soluções primal e dual guardam estreita relação, pois a solução
ótima de qualquer um dos problemas dá a solução ótima do outro (𝑍 =
𝐷).
Assim, em um problema de PL no qual o número de variáveis é menor
do que o número de restrições, podemos reduzir o número de cálculos
se resolvermos o problema dual (isso ocorre pois a quantidade de
cálculos pelo método Simplex depende em grande parte do número de
restrições).
É importante ressaltar que o dual do dual é o primal, o que significa
que a solução ótima dual pode ser usada para obter a solução ótima
primal automaticamente.

37. Propriedades importantes do Primal-Dual
Nesse ponto, vale fazer um resumo das
propriedades entre os problemas dual e primal:
• A solução ótima primal corresponde à solução
ótima dual com 𝑍 = 𝐷 (isso é chamado de versão
forte da teoria da dualidade).
• Considerando um problema de maximização,
para cada solução viável primal e dual, 𝑍 ≤ 𝐷 (ou
seja, a solução viável do primal será sempre
menor ou igual a solução do dual). Ora, como o
valor máximo do primal ocorre para 𝑍 = 𝐷, que
corresponde ao valor mínimo do dual, então,
enquanto estiverem na solução viável, 𝑍 será
sempre menor ou igual a 𝐷. Por analogia, para
um problema de minimização, para cada solução
viável primal e dual, 𝑍 ≥ 𝐷 (ou seja, a solução
viável do primal será sempre maior ou igual a
solução do dual). Isso é denominado versão fraca
da teoria da dualidade.
• A cada iteração, o método Simplex encontra um
par de soluções (um para cada problema), sendo
que a solução primal é viável, contudo a solução
dual não é viável (exceto na última iteração, na
qual obtemos 𝑍 = 𝐷). Ou seja, cada solução viável
básica no primal (não ótima) corresponde a uma
solução básica inviável no dual (isso é
denominado propriedade das soluções
complementares, a qual explicita que se as
soluções básicas no problema primal não forem
ótimas, então as soluções básicas no problema
dual não serão viáveis).
• O coeficiente da variável de decisão 𝑥𝑖 na função
objetivo primal é o valor da variável de folga
correspondente 𝐹𝑖 da restrição 𝑖 na solução dual
(propriedade de complementaridade da folga).

38. Propriedades importantes do Primal-Dual
Exemplo:
Primal:
Dual:

39. Propriedades importantes do Primal-Dual
Colocando as variáveis de folga no primal e no
dual, temos:
Primal:
Que resulta em:
Solução:

40. Propriedades importantes do Primal-Dual
Dual:
Como já vimos, minimizar 𝐷 é igual a maximizar
−𝐷, então:
Sujeito às restrições:
Que resulta em:
Solução:

41. Propriedades importantes do Primal-Dual
Note que a solução do dual (𝑦1 = 𝑦2 = 𝑦3 = 0)
não é viável, pois não atende às restrições (o
lado esquerdo das restrições é menor do que o
lado direito; por exemplo, a restrição 1 resultou
em 0 ≥ 1).
Além disso, note que as variáveis de folga são
negativas (sendo que elas devem ser positivas).
Esse ponto serve para reforçar que “se as
soluções básicas no problema primal não forem
ótimas, então as soluções básicas no problema
dual não serão viáveis”.
Observe ainda que o coeficiente da variável de
decisão 𝑥𝑖 na função objetivo da tabela primal é
o valor da variável de folga correspondente 𝐹𝑖
da restrição 𝑖 na solução dual (e vice-versa).
Além disso, o coeficiente da variável de folga 𝐹𝑖
da função objetivo na tabela primal é o valor da
variável de decisão correspondente 𝑦𝑖 na
solução dual (e vice-versa).

42. Propriedades importantes do Primal-Dual
De forma análoga, os valores das variáveis de
decisão 𝑥𝑖 no primal são iguais aos coeficientes
de 𝐹𝑖 da restrição 𝑖 na tabela dual (e vice-versa).
E ainda, os valores das variáveis de folga 𝐹𝑖 no
primal são iguais aos valores dos coeficientes de
𝑦𝑖 da função objetivo da tabela dual (e vice-
versa).
Por fim, a função objetivo será:
Continuando a solução do primal, com a
entrada da variável 𝑥3 (pois seu coeficiente é -3)
e a saída da variável 𝐹2 (12/4 = 3), após o
pivotamento, será: