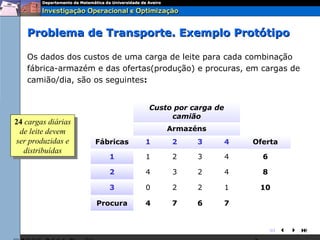
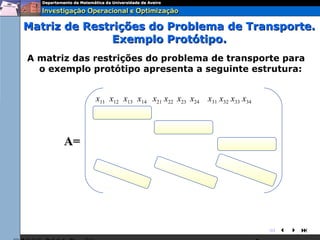
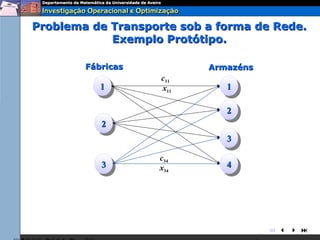
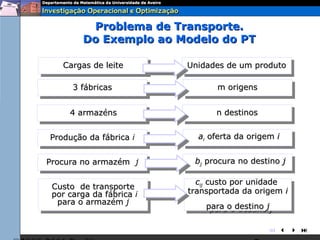
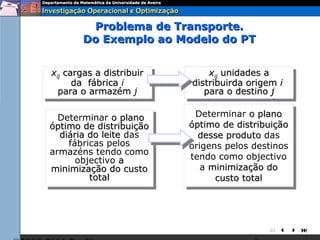
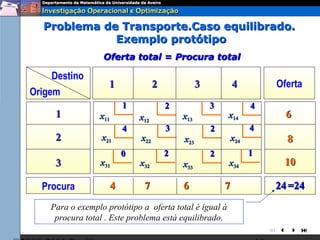
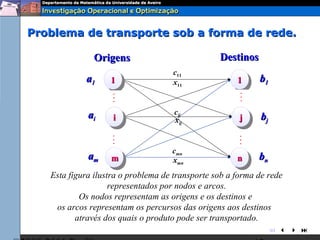
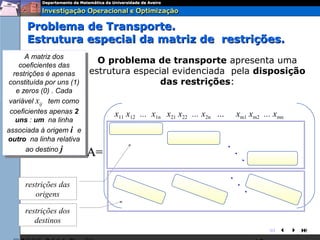
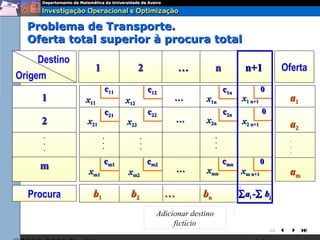
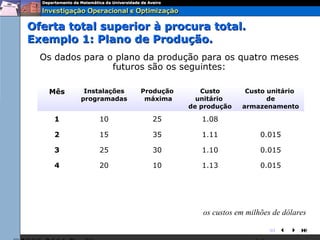
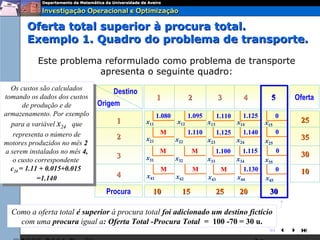
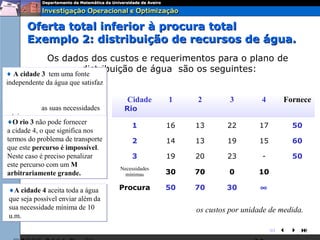
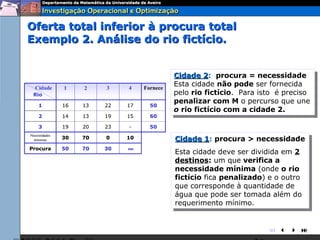
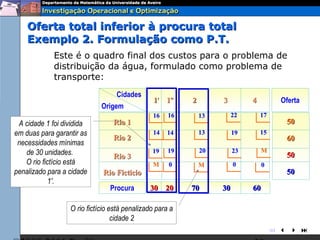
O documento descreve o problema de transporte (PT) e fornece um exemplo protótipo. O PT envolve a distribuição ótima de produtos entre origens e destinos, considerando capacidades e custos de transporte. No exemplo, a distribuição ótima de leite entre fábricas e armazéns é modelada como um PT para minimizar custos totais. A formulação matemática do PT é apresentada.

1. II. Programação Linear (PL)
Capítulo 7.1:
O problema de transporte (PT).
 Definição e apresentação sobre forma de rede.
 Formulação do caso equilibrado e não equilibrado.
Exemplos
 Propriedades fundamentais.


2. Problema de Transporte. Exemplo Protótipo
Um dos principais produtos da firma Lactosal é o leite.
Os pacotes de leites são empacotados
em 3 fábricas
e depois são distribuídos de camião
para quatro armazéns
Conhecendo os custos de transporte, a procura prevista
para cada armazém e as capacidades de produção de
cada fábrica, pretende-se:
OPTIMIZAR O PROGRAMA DE DISTRIBUIÇÃO DIÁRIO
DO LEITE.


3. Problema de Transporte. Exemplo Protótipo
Os dados dos custos de uma carga de leite para cada combinação
fábrica-armazém e das ofertas(produção) e procuras, em cargas de
camião/dia, são os seguintes:
Custo por carga de
camião
24 cargas diárias
24 cargas diárias
de leite devem Armazéns
de leite devem
ser produzidas ee
ser produzidas Fábricas 1 2 3 4 Oferta
distribuídas
distribuídas 1 1 2 3 4 6
2 4 3 2 4 8
3 0 2 2 1 10
Procura 4 7 6 7


4. Formulação do Problema de Transporte.
Exemplo Protótipo.
Custo por carga de
camião
Armazéns
Fábricas 1 2 3 4 Oferta
1 1 2 3 4 6
2 4 3 2 4 8
3 0 2 2 1 10
Procura 4 7 6 7 Minimizar z = x11 + 2 x12 + 3 x13 + 4 x14 +
4 x21 + 3 x22 + 2 x23 + 4 x24 +
2 x32 + 2 x33 + x34
sujeito a:
x11 + x12 + x13+ x14 = 6
x21 + x22 + x23+ x24 = 8
x31 + x32 + x33+ x34 = 10
x11 + x21 + x31 = 4
x12 + x22 + x32 = 7
x13 + x23 + x33 = 6
x14 + x24 + x34 = 7
xij ≥ 0 ( i=1,2,3; j=1,2,3,4 ) 

5. Matriz de Restrições do Problema de Transporte.
Exemplo Protótipo.
A matriz das restrições do problema de transporte para
o exemplo protótipo apresenta a seguinte estrutura:
x11 x12 x13 x14 x21 x22 x23 x24 x31 x32 x33 x34
A=


6. Problema de Transporte sob a forma de Rede.
Exemplo Protótipo.
Fábricas Armazéns
c11
11 x11 11
22
22
33
c34
33 x34 44


7. Problema de Transporte.
Do Exemplo ao Modelo do PT
Cargas de leite
Cargas de leite Unidades de um produto
Unidades de um produto
3 fábricas
3 fábricas m origens
m origens
4 armazéns
4 armazéns n destinos
n destinos
Produção da fábrica i i
Produção da fábrica ai oferta da origem i i
ai oferta da origem
Procura no armazém jj
Procura no armazém bj procura no destino jj
bj procura no destino
cc custo por unidade
ij custo por unidade
Custo de transporte
Custo de transporte ij
por carga da fábrica i i transportada da origem i i
transportada da origem
por carga da fábrica
para o armazém jj
para o armazém para o destino jj
para o destino


8. Problema de Transporte.
Do Exemplo ao Modelo do PT
xij cargas a distribuir
xij cargas a distribuir xij unidades a
xij unidades a
da fábrica ii
da fábrica distribuirda origem ii
distribuirda origem
para o armazém jj
para o armazém para o destino jj
para o destino
Determinar o plano Determinar o plano
Determinar o plano
Determinar o plano óptimo de distribuição
óptimo de distribuição
óptimo de distribuição óptimo de distribuição
diária do leite das
diária do leite das desse produto das
desse produto das
fábricas pelos
fábricas pelos origens pelos destinos
armazéns tendo como origens pelos destinos
armazéns tendo como tendo como objectivo
objectivo a
objectivo a tendo como objectivo
minimização do custo
minimização do custo a minimização do
a minimização do
total
total custo total
custo total


9. Problema de Transporte. Caso Equilibrado.
Oferta total = Procura total
Destino
1 2 … n Oferta
Origem
c11 c12 c1n
1 x11 x12 … x1n a1
c21 c22 c2n
2 x21 x22 … x2n a2
. . . . .
. . . . .
. . . . .
cm1 cm2 cmn
m xm1 xm2 … xmn am
Procura b1 b2 … bn ∑ i =∑ bj
a
Um problema de transporte está equilibrado se
a oferta total é igual à procura total, caso
contrário está não equilibrado.


10. Problema de Transporte.Caso equilibrado.
Exemplo protótipo
Oferta total = Procura total
Destino
1 2 3 4 Oferta
Origem
1 2 3 4
1 x11 x12 x13 x14 6
4 3 2 4
2 x21 x22 x23 x24 8
0 2 2 1
3 x31 x32 x33 x34 10
Procura 4 7 6 7 24 =24
Para o exemplo protótipo a oferta total é igual à
procura total . Este problema está equilibrado.


11. Problema de Transporte.
Formulação como problema de PL.
m n
Minimizar z = ∑∑ cij xij
i =1 j =1
sujeito a:
n restrições de
∑x
j =1
ij = ai , i = 1,2,..., m oferta
restrições de
m procura
∑x
i =1
ij = b j , j = 1,2,..., n
xij ≥ 0 , i = 1,2,..., m , j = 1,2,..., n


12. Problema de transporte sob a forma de rede.
Origens Destinos
c11
a1 11 x11 11 b1
. .
. .
. .
ai cij
ii xij jj bj
. .
. .
. .
cmn
am m
m xmn nn bn
Esta figura ilustra o problema de transporte sob a forma de rede
representados por nodos e arcos.
Os nodos representam as origens e os destinos e
os arcos representam os percursos das origens aos destinos
através dos quais o produto pode ser transportado.


13. Problema de Transporte.
Estrutura especial da matriz de restrições.
A matriz dos
A matriz dos
coeficientes das
O problema de transporte apresenta uma
coeficientes das
restrições ééapenas estrutura especial evidenciada pela disposição
restrições apenas
constituída por uns (1)
constituída por uns (1) das restrições:
eezeros (0) . .Cada
zeros (0) Cada
variável xx tem como
variável ijij tem como
coeficientes apenas 22
coeficientes apenas x11 x12 ... x1n x21 x22 ... x2n … xm1 xm2 ... xmn
uns : :um na linha
uns um na linha
associada ààorigem ii ee
associada origem
outro na linha relativa
outro na linha relativa .
ao destino jj
ao destino A= .
.
.
restrições das .
.
origens
restrições dos
destinos


14. Problema de Transporte.
Oferta total superior à procura total
Destino
1 2 … n n+1 Oferta
Origem
c11 c12 c1n 0
1 x11 x12 … x1n x1 n+1 a1
c21 c22 c2n 0
2 x21 x22 … x2n x2 n+1 a2
. . . .
. . . .
.
. . . .
. .
cm1 cm2 cmn 0
m … xmn
xm1 xm2 xm n+1 am
Procura b1 b2 … bn ∑ a i -∑ b j
Adicionar destino
fictício


15. Oferta total superior à procura total.
Exemplo 1: Plano de Produção.
Uma multinacional produz aviões comerciais para diversas
companhias de aviação. A última etapa no processo de
produção é a produção de motores seguido da sua instalação
no avião.
Para cumprir os contratos estabelecidos deve ser determinado
o plano óptimo de produção dos motores para os próximos
quatro meses.


16. Oferta total superior à procura total.
Exemplo 1: Plano de Produção.
Os dados para o plano da produção para os quatro meses
futuros são os seguintes:
Mês Instalações Produção Custo Custo unitário
programadas máxima unitário de
de produção armazenamento
1 10 25 1.08
2 15 35 1.11 0.015
3 25 30 1.10 0.015
4 20 10 1.13 0.015
os custos em milhões de dólares


17. Oferta total superior à procura total.
Exemplo 1: Plano de Produção.
Este problema pode ser reformulado como um problema de
transporte, tomando como:
 Origem i - produção de motores no mês i
(i =1,2,3,4)
 Destino j - instalação de motores no mês j
(j=1,2,3,4)
 xij - quantidades de motores produzidos no mês i a serem
instalados no mês j
 xij = 0, se i>j (primeiro produzir, depois instalar)
 cij - custo por unidade de produção e armazenamento
 cij= M, se i>j, como não existe custo real associado com estes
dados, podem ser penalizados com um M arbitrariamente
grande.


18. Oferta total superior à procura total.
Exemplo 1. Restrições de ofertas.
As restrições de oferta correspondem à produção de motores
para cada mês i. Estas restrições são de desigualdade
limitadas pela capacidade máxima de produção por mês.
Mês Instalações
programadas
Produção
máxima
Custo
unitário
Custo unitário
de
x11 + x12 + x13+ x14 ≤ 25
1 10 25
de produção
1.08
armazenamento
x21 + x22 + x23+ x24 ≤ 35
2 15 35 1.11 0.015 x31 + x32 + x33+ x34 ≤ 30
3 25 30 1.10 0.015
4 20 10 1.13 0.015
x41 + x42 + x43+ x44 ≤ 10
Como estas restrições são de desigualdade éépreciso introduzir variáveis de
Como estas restrições são de desigualdade preciso introduzir variáveis de
folga para converte-las em restrições de igualdade.
folga para converte-las em restrições de igualdade.
Isto significa que éépreciso introduzir um destino fictício, em que as variáveis
Isto significa que preciso introduzir um destino fictício, em que as variáveis
de folga representam aacapacidade de produção não utilizada por cada mês . .
de folga representam capacidade de produção não utilizada por cada mês


19. Oferta total superior à procura total.
Exemplo 1. Restrições de procuras.
As restrições de procura correspondem ao plano de
instalação para cada mês j. Estas restrições são de igualdade,
correspondendo ao número de instalações requisitadas para
cada mês.
Mês Instalações Produção Custo
unitário
Custo unitário
de
x11 + x21 + x31+ x32 = 10
programadas máxima
de produção armazenamento
1 10 25 1.08
x21 + x22 + x23+ x24 = 15
2 15 35 1.11 0.015 x31 + x32 + x33+ x34 = 25
3 25 30 1.10 0.015
4 20 10 1.13 0.015
x41 + x42 + x43+ x44 = 20
Como ééimpossível produzir motores num mês determinado para serem
Como impossível produzir motores num mês determinado para serem
instalados num mês anterior, todas as variáveis de decisão correspondentes
instalados num mês anterior, todas as variáveis de decisão correspondentes
aa ii>j devem ser nulas. Para obter isto, éépreciso penalizar os custos
>j devem ser nulas. Para obter isto, preciso penalizar os custos
correspondentes aaestas variáveis com um M arbitrariamente grande, tal
correspondentes estas variáveis com um M arbitrariamente grande, tal
como no método do “big M”.
como no método do “big M”.


20. Oferta total superior à procura total.
Exemplo 1. Quadro do problema de transporte.
Este problema reformulado como problema de transporte
apresenta o seguinte quadro:
Os custos são calculados
Os custos são calculados Destino
tomando os dados dos custos
tomando os dados dos custos 1 2 3 4 5 Oferta
de produção eede Origem
de produção de
armazenamento. Por exemplo
armazenamento. Por exemplo 1.080 1.095 1.125
1.110 0
para aavariável xx que 1 x11 x12 x13 x14 x15 25
para variável 24 que
24
representa oonúmero de M 1.110 1.125 1.140 0
representa número de 2 x21 x22 x23 x24 x25
35
motores produzidos no mês 22
motores produzidos no mês
aaserem instalados no mês 4, M M 1.100 1.115 0
serem instalados no mês 4, 3 x31 x32
30
oocusto correspondente x33 x34 x35
custo correspondente
cc ==1.11 ++0.015+0.015
24 1.11 0.015+0.015 M M M 1.130 0 10
24
=1.140 4 x41 x42 x43 x44 x45
=1.140
Procura 10 15 25 20 30
30
Como a oferta total é superior à procura total foi adicionado um destino fictício
com uma procura igual a: Oferta Total -Procura Total = 100 -70 = 30 u.


21. Problema de Transporte.
Oferta total inferior à procura total
Destino
1 2 … n Oferta
Origem
c11 c12 c1n
1 x11 x12 … x1n a1
c21 c22 c2n
2 x21 x22 … x2n a2
. . . . .
. . . .
. .
. . . .
cm1 cm2 cmn
m xm1 xm2 … xmn
am
0 0 0
m+1 xm+1,1 xm+1,2
…
xm+1,n ∑ bj -∑ ai
Procura b1 b2 … bn Origem fictícia


22. Oferta total inferior à procura total
Exemplo 2: distribuição de recursos de agua.
Uma empresa administra a distribuição de água duma região.
Para isto é preciso canalizar a água de 3 rios que estão
situados fora da região e distribui-la para 4 cidades.
Agora o gerente da empresa pretende distribuir toda a água
disponível dos 3 rios para as 4 cidades, de forma a pelo
menos satisfazer as necessidades essenciais de cada uma,
minimizando o custo total.


23. Oferta total inferior à procura total
Exemplo 2: distribuição de recursos de água.
Os dados dos custos e requerimentos para o plano de
distribuição de água são os seguintes:
♦ A cidade 3 tem uma fonte
♦ A cidade 3 tem uma fonte
independente da água que satisfaz
Cidade 1 2 3 4 Fornece
as suas necessidades Rio
mínimas
♦O rio 3 não pode fornecer
1 16 13 22 17 50
a cidade 4, o que significa nos
termos do problema de transporte 2 14 13 19 15 60
que este percurso é impossível.
Neste caso é preciso penalizar 3 19 20 23 - 50
este percurso com um M Necessidades
arbitrariamente grande. mínimas 30 70 0 10
♦A cidade 4 aceita toda a água Procura 50 70 30 ∞
que seja possível enviar além da
sua necessidade mínima de 10 os custos por unidade de medida.
u.m.


24. Oferta total inferior à procura total
Exemplo 2: distribuição de recursos de água.
Este problema pode ser reformulado como um problema de
transporte, tomando como:
 Origem i – o rio i (i =1,2,3)
 Destino j – a cidade j (j=1,2,3,4)
 xij - quantidade de água a enviar do rio i para a cidade j
 cij - custo unitário da distribuição da água do rio i para a cidade j


25. Oferta total inferior à procura total
Exemplo 2. Restrições de ofertas.
As restrições de oferta correspondem às restrições dos rios
(origens). Como deverá ser distribuída toda a água disponível
dos 3 rios, estas 3 restrições são de igualdade, uma por cada
rio.
Cidade 1 2 3 4 Fornece
Rio
1 16 13 22 17 50 x11 + x12 + x13+ x14 = 50
2 14 13 19 15 60 x21 + x22 + x23+ x24 = 60
3 19 20 23 - 50
x31 + x32 + x33+ x34 = 50
Necessidades
mínimas 30 70 0 10
Procura 50 70 30 ∞


26. Oferta total inferior à procura total
Exemplo 2. Restrições de procura.
As restrições de procura determinam a quantidade de água que
deve ser fornecida a cada cidade, e têm limites superiores e inferiores
(excepto a cidade 2, onde coincidem a procura com a necessidade
mínima).
Cidade 1: procura > necessidade
Cidade1 procura > necessidade
1:
1
Cidade 1 2 3 4 Fornece
Rio
x11 + x21 + x31 ≥ 30 limite inferior
1 16 13 22 17 50
x11 + x21 + x31 ≤ 50 limite superior
2 14 13 19 15 60
3 19 20 23 - 50 Cidade 2: procura = necessidade
Cidade2 procura = necessidade
2:
2
Necessidades
30 70 0 10
mínimas x12 + x22 + x32 = 70
Procura 50 70 30 ∞
Cidade 3: procura > necessidade
Cidade3 procura > necessidade
3:
3
O limite superior para a cidade 4 pode ser calculado
como a diferença entre a oferta total (50+ 60+50=160) x13+ x23 + x33 ≤ 30 limite superior
e a soma das necessidades mínimas para as restantes Cidade 4: procura > necessidade
cidades (30+ 70 =100) ⇒ 160 - 100 = 60 unidades. Cidade4 procura > necessidade
4:
4
(a quantidade máxima que pode receber a cidade 4 x14 + x24 + x34 ≥ 10 limite inferior
para além da necessidade mínima ) x14 + x24 + x34 ≤ 60 limite superior


27. Oferta total inferior à procura total
Exemplo 2. Quadro do problema de transporte.
Cidades
1 2 3 4 Oferta
Origem
16 13 22 17
Rio 1 x11 x12 x13 x14 50
14 13 19 15
Rio 2 x21 x22 x23 x24 60
19 20 23 M
Rio 3 x31 x32 x33 x34 50
0 0 0 0
Rio Ficticio x41 x42 x43 x44 50
Procura 50 70 30 60
Como a oferta total é inferior à procura total foi adicionada
uma origem fictícia com uma oferta igual a:
Procura Total -Oferta Total = 210 -160 = 50 unidades.


28. Oferta total inferior à procura total
Exemplo 2. Análise do rio fictício.
Para satisfazer as necessidades mínimas de água é preciso re-analisar os dados
para cada cidade de forma a garantir que o mínimo procurado não seja fornecido
pelo rio fictício.
Cidade 3: Como não tem
Cidade3 3: Como não tem
3
necessidade mínima, então não é
necessidade mínima, então não é
Cidade 1 2 3 4 Fornece
Rio preciso alterar nada.
preciso alterar nada.
1 16 13 22 17 50
2 14 13 19 15 60
Cidade 4: procura > necessidade
Cidade4 procura > necessidade
4:
4
3 19 20 23 - 50
(60 > 10). Como o rio fictício
(60 > 10). Como o rio fictício
Necessidades
30 70 0 10
mínimas fornece apenas 50 unidades, pelo
fornece apenas 50 unidades, pelo
Procura 50 70 30 ∞ menos fica garantido que as 10
menos fica garantido que as 10
unidades mínimas não podem ser
unidades mínimas não podem ser
obtidas deste rio. Não é preciso
obtidas deste rio. Não é preciso
alterar nada.
alterar nada.


29. Oferta total inferior à procura total
Exemplo 2. Análise do rio fictício.
Cidade 2: procura = necessidade
Cidade2 procura = necessidade
2:
2
Cidade 1 2 3 4 Fornece
Esta cidade não pode ser fornecida
Esta cidade não pode ser fornecida
Rio pelo rio fictício. Para isto é preciso
pelo rio fictício. Para isto é preciso
penalizar com M o percurso que une
penalizar com M o percurso que une
1 16 13 22 17 50
o rio fictício com a cidade 2.
o rio fictício com a cidade 2.
2 14 13 19 15 60
3 19 20 23 - 50
Necessidades
mínimas 30 70 0 10 Cidade 1: procura > necessidade
Cidade1 procura > necessidade
1:
1
Procura 50 70 30 ∞
Esta cidade deve ser dividida em 2
Esta cidade deve ser dividida em 2
destinos: um que verifica a
destinos: um que verifica a
necessidade mínima (onde o rio
necessidade mínima (onde o rio
fictício fica penalizado) e o outro
fictício fica penalizado) e o outro
que corresponde à quantidade de
que corresponde à quantidade de
água que pode ser tomada além do
água que pode ser tomada além do
requerimento mínimo.
requerimento mínimo.


30. Oferta total inferior à procura total
Exemplo 2. Formulação como P.T.
Este é o quadro final dos custos para o problema de
distribuição da água, formulado como problema de
transporte:
Cidades
1' 1'' 2 3 4 Oferta
Origem
16 16 13 22 17
A cidade 1 foi dividida Rio 1 50
em duas para garantir as 14 14 13 19 15
Rio 2 60
necessidades mínimas
de 30 unidades. 19 19 20 23 M
Rio 3 50
O rio fictício está M 0 M 0 0
penalizado para a cidade Rio Ficticio 50
1'.
Procura 30 20 70 30 60
O rio fictício está penalizado para a
cidade 2


31. Problema de Transporte. Propriedades
fundamentais(1).
 Se um problema de transporte está equilibrado, i.e., a oferta
total é igual à procura total, então tem sempre soluções
admissíveis.
 Se um problema de transporte não está equilibrado,i.e., a oferta
total não é igual à procura total, então pode ser introduzida
uma origem ou um destino fictício para converter as restrições
de desigualdade em igualdade e poder obter assim um problema
equilibrado.
 O problema de transporte tem sempre óptimo finito.
 Qualquer SBA do problema de transporte tem no máximo m+n-1
variáveis básicas
Do total de m+n equações só m+n-1 são linearmente independentes, existindo
sempre uma equação redundante, i.e., uma equação pode ser obtida como
combinação linear das restantes.


32. Problema de Transporte. Propriedades
fundamentais(2).
A base correspondente a qualquer SBA do problema de
transporte é uma matriz triangular.
1 1 0 …0 0
0 1 1 …0 0
0 0 1 …0 0
B= ...
0 0 0 …1 1
0 0 0 …0 1
 Se as quantidades das ofertas e procuras são valores inteiros,
então qualquer SBA tem sempre valores inteiros.
Como a matriz da base é uma matriz triangular composta por 0 e 1, a resolução
do sistema conduz necessariamente a uma solução cujas variáveis assumem
apenas valores inteiros, pois apenas exige adições e subtracções.


33. Base e Solução Básica Admissível para o PT.
Minimizar z = x11 + 2 x12 + 3 x13 + 4 x14 +
4 x21 + 3 x22 + 2 x23 + 4 x24 +
sujeito a:
2 x32 + 2 x33 + x34
Como m=3 e n=4 e a característica de A, c(A)=m+n-1=6,
=
qualquer base B tem dimensão 6x6. Uma base pode ser
x11 + x12 + x13+ x14 6
x21 + x22 + x23+ x24 = 8
x31 + x32 + x33+ x34 = 10
x11
x12
+ x21
+ x22
+ x31
+ x32
=
=
4
7 obtida, por exemplo, tomando as colunas P11, P12, P22, P23,
x13 + x23 + x33 = 6
x14 + x24 + x34 = 7
P33, P34 e eliminando à restrição 4.
xij ≥ 0 ( i=1,2,3; j=1,2,3,4 )
P11 P12 P13 P14P21P22P23P24P31P32P33P34
P11 P12P22P23P33P34
(1) 1 1 1 1 0 0 0 0 0 0 0 0
(1) 1 1 0 0 0 0
(2) 0 0 0 0 1 1 1 1 0 0 0 0
(2) 0 0 1 1 0 0
A= (3) 0 0 0 0 0 0 0 0 1 1 1 1
B= (3) 0 0 0 0 1 1
(4) 1 0 0 0 1 0 0 0 1 0 0 0
(5) 0 1 1 0 0 0
(5) 0 1 0 0 0 1 0 0 0 1 0 0
(6) 0 0 0 1 1 0
(6) 0 0 1 0 0 0 1 0 0 0 1 0
(7) 0 0 0 0 0 1
(7) 0 0 0 1 0 0 0 1 0 0 0 1
Trocando as P11 P12P22P23P33P34
linhas obtém-se
uma matriz B
(1) 1 1 0 0 0 0
triangular (5) 0 1 1 0 0 0
B= (2) 0 0 1 1 0 0
(6) 0 0 0 1 1 0
(3) 0 0 0 0 1 1
(7) 0 0 0 0 0 1


34. Uma Solução básica Admissível para o PT.
Como a matriz B é triangular a solução do sistema é imediata:
XB xx =7
34 =7
34
P11 P12P22P23P33P34
x11 6 x33 + x34 =10 xx =3
(1) 1 1 0 0 0 0 33 =3
(5) 0 1 1 0 0 0 x12 7
33
(2) 0 0 1 1 0 0 x22 = 8 x23 + x33 = 6 xx =3
23 =3
23
(6) 0 0 0 1 1 0 x23 6
(3) 0 0 0 0 1 1 10 x22 + x23 = 8 xx =5
22 =5
x33 22
(7) 0 0 0 0 0 1
x34 7
x12 + x22 = 7 xx =2
12 =2
12
x11 + x12 = 6 xx =4
11 =4
11
Uma SBA do problema é: X = (4, 2, 0, 0, 0, 5, 3, 0, 0, 0, 3, 7)
Uma SBA do problema é: X = (4, 2, 0, 0, 0, 5, 3, 0, 0, 0, 3, 7)
