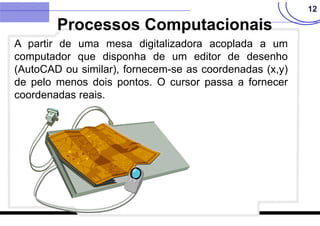
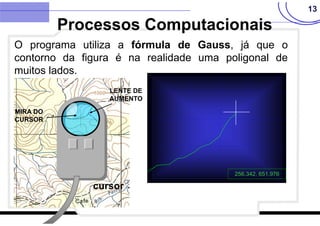
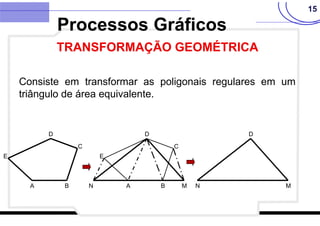
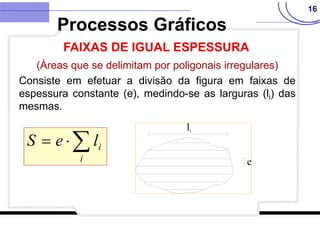
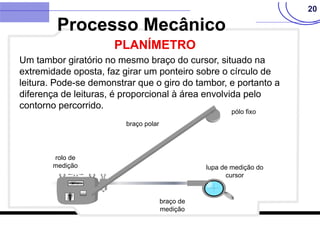
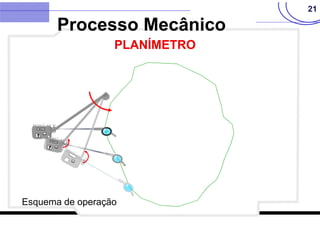
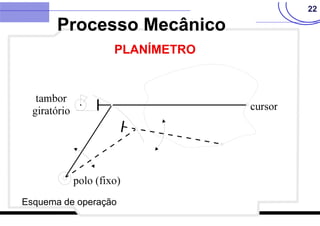
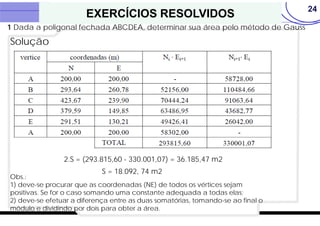
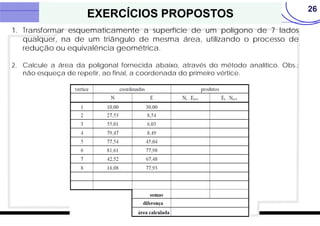
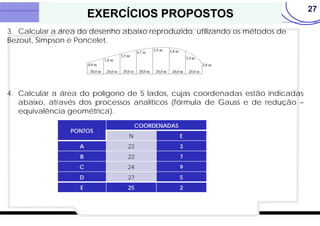
O documento discute vários métodos para calcular a área de polígonos, incluindo métodos analíticos, computacionais, gráficos e mecânicos. Os principais métodos analíticos são a fórmula de Gauss, o método de Bezout, o método de Poncelet e o método de Simpson. Os processos computacionais usam a fórmula de Gauss com coordenadas digitadas. Os métodos gráficos incluem transformações geométricas, divisão em faixas e quadrículas. O planímetro é o principal




![7
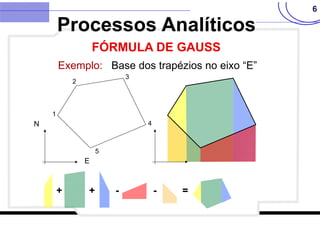
FÓRMULA DE GAUSS
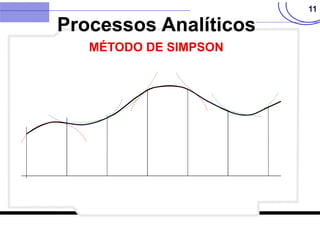
Processos Analíticos
Exemplo: Base dos trapézios no eixo “E”
N1
N1
N2
N2
N3
N3
N4
N4
N5
N5
E1-E5 (<0)
E2 –E1
E3-E2
E4-E3
E5-E4 (<0)
S = 0,5 x [ (E2-E1) x (N1+N2)
+ (E3-E2) x (N3+N2)
+ (E4-E3) x (N4+N3)
+ (E5-E4) x (N5+N4)
+ (E1-E5) x (N1+N5)]
(uma das formas
da fórmula de Gauss)](https://image.slidesharecdn.com/aula11calculodeareas-220923184706-6e3683ce/85/Calculo-de-areas-pdf-7-320.jpg)