Este documento descreve diferentes tipos de funções matemáticas, incluindo suas propriedades e representações gráficas. Aborda funções constantes, identidade, do primeiro grau, módulo, quadrática, polinomial, racional, exponencial, logarítmica, trigonométricas, hiperbólicas e periódicas.

1. ´
´
UNIVERSIDADE TECNOLOGICA FEDERAL DO PARANA
Campus Corn´lio Proc´pio
e
o
FUNCOES
¸˜
ARMANDO PAULO DA SILVA
FERNANDO BRITO
GABRIELA CASTRO SILVA CAVALHEIRO
´
MARCIA REGINA PIOVESAN
THIAGO DE SOUZA PINTO
Corn´lio Proc´pio - PR, 2012
e
o

2. Sum´rio
a
1. Fun¸oes
c˜
4
1.1. Opera¸oes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
6
1.2. Fun¸oes especiais
c˜
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.2.1. Fun¸ao constante . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
8
1.2.2. Fun¸ao identidade . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
8
1.2.3. Fun¸ao do primeiro grau . . . . . . . . . . . . . . . . . . . . . . .
c˜
9
1.2.4. Fun¸ao m´dulo . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
o
10
1.2.5. Fun¸ao quadr´tica . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
a
10
1.2.6. Fun¸ao polinomial . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
11
1.2.7. Fun¸ao racional . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
12
1.28. Fun¸ao exponencial . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
13
1.2.9. Fun¸ao logar´
c˜
ıtmica . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.3. Fun¸oes trigonom´tricas . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
e
15
1.3.1. Fun¸ao seno . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
15
1.3.2. Fun¸ao cosseno . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
16
1.3.3. Fun¸ao tangente . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
17
1.3.4. Fun¸ao cotangente . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
18
1.3.5. Fun¸ao secante . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
19
1.3.6. Fun¸ao cossecante . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
20
1.4. Fun¸oes hiperb´licas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
o
21
1.4.1. Seno hiperb´lico e cosseno hiperb´lico . . . . . . . . . . . . . . . .
o
o
22
1.4.2. Fun¸oes tangente, cotangente, secante e cossecante hiperb´licas . .
c˜
o
22
1.5. Fun¸ao peri´dica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
o
24
2

3. 1.6. Fun¸ao par e fun¸ao ´
c˜
c˜ ımpar . . . . . . . . . . . . . . . . . . . . . . . . . .
25
1.7. Fun¸ao inversa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
25
1.7.1. Fun¸ao sobrejetora . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
26
1.7.2. Fun¸ao injetora . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
26
1.7.3. Fun¸ao bijetora . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c˜
27
2. Aplica¸oes
c˜
31
Referˆncias
e
35

4. 1. Fun¸oes
c˜
Antes de definirmos formalmente o que ´ uma fun¸ao, podemos pensar em um valor
e
c˜
que depende de outro. Por exemplo:
1. Uma rela¸ao que expresse a area de um quadrado em fun¸ao do comprimento do
c˜
´
c˜
lado.
2. A area A de um c´
´
ırculo depende de seu raio r. A lei que conecta r e A ´ dada pela
e
equa¸ao A = πr 2 . A cada n´mero real r positivo existe associado um unico valor
c˜
u
´
de A, e dizemos que A ´ uma fun¸ao de r.
e
c˜
Defini¸˜o: Sejam A e B subconjuntos de R. Uma fun¸ao f : A → B ´ uma lei ou
ca
c˜
e
regra que a cada elemento de A faz corresponder um unico elemento de B. O conjunto
´
A ´ chamado dom´
e
ınio de f e ´ denotado por D(f ). B ´ chamado de contra-dom´
e
e
ınio ou
campo de valores de f .
Escrevemos:
f :A→B
x → f (x)
IMPORTANTE:
a) n˜o deve haver exce¸oes: se f tem o conjunto A como dom´
a
c˜
ınio, a regra deve fornecer
f (x) para todo x ∈ A;
b) n˜o deve haver ambig¨idades: a cada x ∈ A, a regra deve fazer corresponder um unico
a
u
´

5. 5
f (x) ∈ B.
Exemplos:
1. Sejam A = {1, 2, 3, 4} e B = {2, 3, 4, 5}.
(a) f : A → B dada pelo diagrama abaixo ´ uma fun¸ao.
e
c˜
(b) g : A → B
x→x+1
´ uma fun¸ao de A em B.
e
c˜
2. Sejam A = {3, 4, 5} e B = {1, 2}.
(a) f : A → B dada pelo diagrama abaixo n˜o ´ uma fun¸ao de A em B.
a e
c˜
(b) g : A → B
x→x−3
N˜o ´ uma fun¸ao de A em B, pois o elemento 3 ∈ A n˜o tem correspondente
a e
c˜
a
em B.

6. 6
Defini¸˜o: Seja f : A → B.
ca
i) Dado x ∈ A, o elemento f (x) ∈ B ´ chamado de valor da fun¸ao f no ponto x ou
e
c˜
de imagem de x por f .
ii) O conjunto de todos os valores assumidos pela fun¸ao ´ chamado conjunto imagem
c˜ e
de f e ´ denotado por Im(f ).
e
CUIDADO!
a) N˜o se deve confundir f com f (x): f ´ a fun¸ao, enquanto que f (x) ´ a imagem que
a
e
c˜
e
a fun¸ao assume em x.
c˜
b) N˜o confunir f (x) com f (A): f (x) ´ a imagem de x ∈ A por f , enquanto f (A) ´ o
a
e
e
conjunto
{f (x) ∈ B|x ∈ A}
que ´ a imagem direta de A por f (ou simplesmente, a imagem de f ).
e
Defini¸˜o: Seja f uma fun¸ao. O gr´fico de f ´ o conjunto de todos os pontos (x, f (x))
ca
c˜
a
e
de um plano coordenado, onde x pertence ao dom´
ınio de f .
G(f ) = {(x, f (x)) | x ∈ D(f )}.
1.1. Opera¸oes
c˜
Defini¸˜o: Dadas as fun¸oes f e g, sua soma f + g, diferen¸a f − g, produto f · g e
ca
c˜
c
quociente f /g, s˜o definidas por:
a
i) (f + g)(x) = f (x) + g(x)
ii) (f − g)(x) = f (x) − g(x)

7. 7
iii) (f · g)(x) = f (x) · g(x)
f (x)
f
, desde que g(x) = 0.
iv) ( )(x) =
g
g(x)
O dom´
ınio das fun¸oes f + g, f − g, f · g ´ a intersec¸ao dos dom´
c˜
e
c˜
ınios de f e g.
O dom´
ınio de f /g ´ a intersec¸ao dos dom´
e
c˜
ınios de f e g, excluindo-se os pontos onde
g(x) = 0.
Defini¸˜o: Se f ´ uma fun¸ao e k ´ um n´mero real, definimos a fun¸ao kf por
ca
e
c˜
e
u
c˜
(kf (x)) = kf (x).
O dom´
ınio de kf coincide com o dom´
ınio de f .
Defini¸˜o: Dadas duas fun¸oes f e g, a fun¸ao composta de g com f , denotada por
ca
c˜
c˜
g ◦ f , ´ definida por
e
(g ◦ f )(x) = g(f (x)).
O dom´ de g ◦ f ´ o conjunto de todos os pontos x no dom´ de f tais que f (x) est´
ınio
e
ınio
a
no dom´
ınio de g.
Simbolicamente,
D(g ◦ f ) = {x ∈ D(f ) | f (x) ∈ D(g)}.
Veja o diagrama abaixo:

8. 8
1.2. Fun¸oes especiais
c˜
Veremos agora algumas fun¸oes importantes, bem como suas principais caracter´
c˜
ısticas.
1.2.1. Fun¸˜o constante
ca
´
E toda fun¸ao do tipo f (x) = k, que associa a qualquer n´mero real x um mesmo
c˜
u
n´mero real k. A representa¸ao gr´fica ser´ sempre uma reta paralela ao eixo dos x,
u
c˜
a
a
passando por y = k.
• O dom´
ınio da fun¸ao f (x) = k ´ D(f ) = R.
c˜
e
• O conjunto imagem ´ o conjunto unit´rio Im(f ) = {k}.
e
a
1.2.2. Fun¸˜o identidade
ca
´
E a fun¸ao f : R → R definida por f (x) = x.
c˜
• O gr´fico desta fun¸ao ´ uma reta bissetriz do primeiro e terceiro quadrantes.
a
c˜ e
• O dom´
ınio de f (x) = x ´ D(f ) = R
e

9. 9
• O conjunto imagem ´ Im(f ) = R.
e
1.2.3. Fun¸˜o do primeiro grau
ca
Fun¸ao do primeiro grau ´ toda fun¸ao que associa a cada n´mero real x o n´mero
c˜
e
c˜
u
u
real ax + b, a = 0. Os n´meros reais a e b s˜o chamados, respectivamente, de coeficiente
u
a
angular e linear.
Uma fun¸ao f ´ crescente quando, a medida que x cresce, f (x) tamb´m
c˜
e
`
e
cresce. Quando f (x) decresce a medida que x cresce, dizemos que a fun¸ao ´
`
c˜ e
decrescente.
Quando a > 0, a fun¸ao f (x) = ax + b ´ crescente e quando a < 0, a fun¸ao
c˜
e
c˜
f (x) = ax + b ´ decrescente.
e
A fun¸ao f (x) = ax + b, a, b ∈ R ´ chamada de fun¸ao afim por muitos autores. Os
c˜
e
c˜
seguintes casos s˜o casos particulares:
a
i) Fun¸ao do primeiro grau, quando a = 0.
c˜
ii) Fun¸ao linear, quando a = 0 e b = 0.
c˜
iii) Fun¸ao constante, quando a = 0.
c˜

10. 10
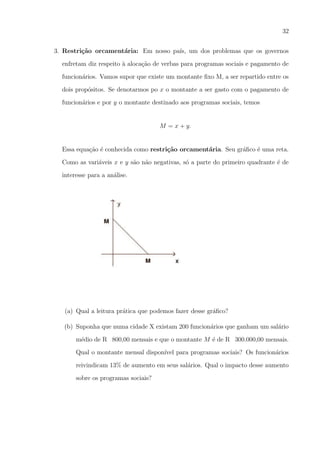
1.2.4. Fun¸˜o m´dulo
ca
o
A fun¸ao definida por y = |x| chama-se fun¸ao m´dulo. O seu dom´
c˜
c˜
o
ınio ´ o conjunto
e
D(f ) = R e o conjunto imagem ´ Im(f ) = [0, +∞].
e
• O gr´fico de f (x) = |x| ´
a
e
1.2.5. Fun¸˜o quadr´tica
ca
a
A fun¸ao f : A → B dada por f (x) = ax2 + bx + c, a = 0, ´ chamada fun¸ao do
c˜
e
c˜
segundo grau ou fun¸ao quadr´tica.
c˜
a
• O dom´
ınio de f ´ D(f ) = R.
e
• O gr´fico de uma fun¸ao quadr´tica ´ uma par´bola com eixo de simetria paralelo ao
a
c˜
a
e
a
eixo dos y. Se o coeficiente de x2 for positivo (a > 0), a par´bola tem a concavidade
a
voltada para cima. Se a < 0, a par´bola tem a concavidade voltada para baixo.
a
• A intersec¸ao do eixo de simetria com a par´bola ´ um ponto chamado v´rtice, o qual
c˜
a
e
e
´ dado por
e
V = (−
∆
b
, − ).
2a 4a

11. 11
• A intersec¸ao da par´bola com o eixo dos x define os zeros da fun¸ao. No quadro
c˜
a
c˜
seguinte caracterizamos as diversas possibilidades.
1.2.6. Fun¸˜o polinomial
ca
´
E a fun¸ao f : R → R definida por f (x) = a0 + ax + a2 x2 + . . . + an xn , onde
c˜
1
a0 , a1 , a2 , . . . , an , a0 = 0, s˜o n´meros reais chamados coeficientes e n inteiro n˜o negativo,
a u
a
determina o grau da fun¸ao.
c˜
• O dom´ ´ sempre o conjunto dos n´meros reais.
ınio e
u
• O gr´fico da fun¸ao polinomial ´ uma curva que pode apresentar pontos de m´ximos e
a
c˜
e
a
m´
ınimos.

12. 12
Exemplos:
1. A fun¸ao constante f (x) = k ´ uma fun¸ao polinomial de grau zero.
c˜
e
c˜
2. A fun¸ao f (x) = ax + b, a = 0 ´ uma fun¸ao polinomial de 10 grau.
c˜
e
c˜
3. A fun¸ao quadr´tica f (x) = ax2 + bx + c, a = 0, ´ uma fun¸ao polinomial do 20
c˜
a
e
c˜
grau.
4. A fun¸ao f (x) = 5x2 − 6x + 7 ´ uma fun¸ao polinomial de grau 5.
c˜
e
c˜
1.2.7. Fun¸˜o racional
ca
p(x)
´
,
E a fun¸ao definida como o quociente de duas fun¸oes polinomiais, isto ´, f (x) =
c˜
c˜
e
q(x)
onde p(x) e q(x) s˜o polinˆmios e q(x) = 0.
a
o
• O dom´
ınio da fun¸ao racional ´ o conjunto dos n´meros reais excluindo aqueles x tais
c˜
e
u
que q(x) = 0.
Exemplos:
1. A fun¸ao f (x) =
c˜
x−1
´ fun¸ao racional de dom´
e
c˜
ınio D(f ) = R − {−1}.
x+1

13. 13
2. A fun¸ao f (x) =
c˜
(x2 + 3x − 4)(x2 − 9)
´ racional de dom´ D(f = R−{−4, −3, 3}
e
ınio
(x2 + x − 12)(x + 3)
1.2.8. Fun¸˜o exponencial
ca
Chamamos de fun¸ao exponencial de base a a fun¸ao f de R em R que associa a cada
c˜
c˜
x real o n´mero real ax , sendo a um n´mero real, 0 < a = 1.
u
u
• O dom´
ınio da fun¸ao exponencial ´ D(f ) = R.
c˜
e
• A imagem da fun¸ao exponencial ´ Im(f ) = (0, ∞).
c˜
e
• Com rela¸ao ao gr´fico da fun¸ao f (x) = ax podemos afirmar:
c˜
a
c˜
1. a curva que o representa est´ toda acima do eixo das abcissas, pois y = ax > 0 para
a
todo x ∈ R;
2. corta o eixo das ordenadas no ponto (0, 1);
3. f (x) = ax ´ crescente se a > 1 e decrescente se 0 < a < 1.
e

14. 14
1.2.9. Fun¸˜o logar´
ca
ıtmica
Dado um n´mero real a (0 < a = 1), chamamos fun¸ao logar´
u
c˜
ıtmica de base a a fun¸ao
c˜
u
de R∗ em R que se associa a cada x o n´mero loga x.
+
• D(f ) = R∗ e Im(f ) = R.
+
• Com rela¸ao ao gr´fico da fun¸ao f (x) = loga x, (0 < a = 1) podemos afirmar:
c˜
a
c˜
1. est´ todo a direita do eixo y;
a
`
2. corta o eixo das abscissas no ponto (1, 0);
3. f (x) = loga x ´ crescente se a > 1 e decrescente se 0 < a < 1;
e

15. 15
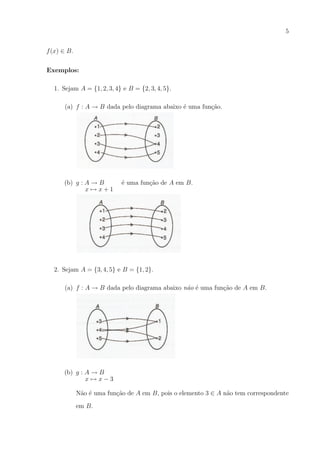
1.3. Fun¸oes trigonom´tricas
c˜
e
1.3.1. Fun¸˜o seno
ca
Seja x um n´mero real. Marcamos um angulo com medida x radianos na circunu
ˆ
ferˆncia unit´ria com centro na origem.
e
a
Seja P o ponto de intersec¸ao do lado terminal do angulo x, com essa circunferˆncia.
c˜
ˆ
e
Denominamos seno de x a ordenada OP1 do ponto P em rela¸ao ao sistema U OV .
c˜
Definimos a fun¸ao seno como a fun¸ao de R em R que a cada x ∈ R faz corresponder
c˜
c˜
o n´mero real y = sen x.
u
• O dom´
ınio da fun¸ao seno ´ R e o conjunto imagem ´ o interevalo [−1, 1]
c˜
e
e
• Em alguns intervalos sen x ´ crescente e em outros ´ decrescente. Por exemplo: nos
e
e
3π
π 3π
π
e
a
e
intervalos [0, ] e [ , 2π] sen x, ´ crescente. J´ no intervalo, [ , ] ela ´ decrescente.
2
2
2 2
• O gr´fico da fun¸ao f (x) = sen(x) ´ denominado sen´ide.
a
c˜
e
o

16. 16
1.3.2. Fun¸˜o cosseno
ca
Seja x um n´mero real. Denominamos cosseno de x a absissa OP2 do ponto P em
u
rela¸ao ao sistema U OV .
c˜
Definimos a fun¸ao cosseno como a fun¸ao f de R em R que a cada x ∈ R faz
c˜
c˜
corresponder o n´mero real y = cos x.
u
• O dom´
ınio da fun¸ao cosseno ´ R e o conjunto imagem ´ o intervalo [−1, 1]
c˜
e
e
• Em alguns intervalos cos x ´ crescente e em outros ´ decrescente. Por exemplo, no
e
e
intervalo [0, π] a fun¸ao f (x) = cos x ´ decrescente. J´ no intervalo [π, 2π], ela ´ crescente.
c˜
e
a
e

17. 17
• O gr´fico da fun¸ao f (x) = cos x ´ denominado cossen´ide.
a
c˜
e
o
1.3.3. Fun¸˜o tangente
ca
Definimos a fun¸ao tangente como a fun¸ao f de R − {
c˜
c˜
π
+ kπ, k ∈ Z} em R que a
2
cada x ∈ R faz corresponder o n´mero real y = tg x.
u
π
• O dom´ da fun¸ao tangente ´ R − { + kπ, k ∈ Z} e o conjunto imagem ´ o conjunto
ınio
c˜
e
e
2
R
• O gr´fico da fun¸ao tg x ´ da seguinte forma:
a
c˜
e

18. 18
1.3.4. Fun¸˜o cotangente
ca
Definimos a fun¸ao cotangente como a fun¸ao f de R − {kπ, k ∈ Z} em R que a cada
c˜
c˜
x ∈ R faz corresponder o n´mero real y = cotg x.
u
• O dom´
ınio da fun¸ao cotangente ´ R − {kπ, k ∈ Z} e o conjunto imagem ´ o conjunto
c˜
e
e
R
• O gr´fico da fun¸ao cotg x ´ da seguinte forma:
a
c˜
e

19. 19
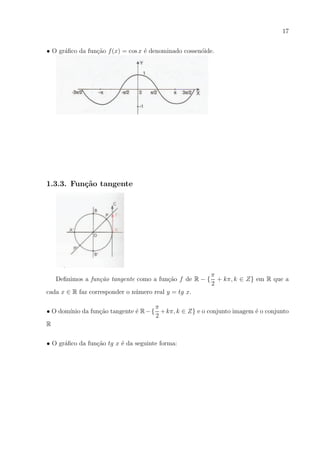
1.3.5. Fun¸˜o secante
ca
π
Definimos a fun¸ao secante como a fun¸ao f de R − { + kπ, k ∈ Z} em R que a cada
c˜
c˜
2
x ∈ R faz corresponder o n´mero real y = sec x.
u
• O dom´
ınio da fun¸ao cotangente ´ R − {
c˜
e
conjunto (−∞, 1]
π
+ kπ, k ∈ Z} e o conjunto imagem ´ o
e
2
[1, +∞)
• O gr´fico da fun¸ao sec x ´ da seguinte forma:
a
c˜
e

20. 20
1.3.6. Fun¸˜o cossecante
ca
Definimos a fun¸ao cossecante como a fun¸ao f de R − {kπ, k ∈ Z} em R que a cada
c˜
c˜
x ∈ R faz corresponder o n´mero real y = cossec x.
u
• O dom´
ınio da fun¸ao cotangente ´ R − {kπ, k ∈ Z} e o conjunto imagem ´ o conjunto
c˜
e
e
(−∞, 1]
[1, +∞)
• O gr´fico da fun¸ao cossec x ´ da seguinte forma:
a
c˜
e

21. 21
1.4. Fun¸oes hiperb´licas
c˜
o
As express˜es exponenciais
o
ex − e−x
2
e
ex + e−x
2
ocorrem freq¨entemente na Matem´tica Aplicada.
u
a
Estas express˜es definem, respectivamnte, as fun¸oes seno hiperb´lico de x e cosseno
o
c˜
o
hiperb´lico de x. O comportamento dessas fun¸oes nos leva a fazer uma analogia com as
o
c˜
fun¸oes trigonom´tricas.
c˜
e

22. 22
1.4.1. Seno hiperb´lico e cosseno hiperb´lico
o
o
A fun¸ao seno hiperb´lico, denotada por senh, e a fun¸ao cosseno hiperb´lico, denoc˜
o
c˜
o
tada por cosh, s˜o definidas, respectivamente por
a
senh x =
ex − e−x
2
e
cosh x =
ex + e−x
.
2
O dom´
ınio e a imagem das fun¸oes senh e cosh s˜o:
c˜
a
D(senh) = (−∞, +∞),
D(cosh) = (−∞, +∞),
Im(senh) = (−∞, +∞) e
Im(cosh) = [1, +∞).
1.4.2. Fun¸oes tangente, cotangente, secante e cossecante hiperb´licas
c˜
o
As fun¸oes tangente, cotangente, secante e cossecante hiperb´licas, denotadas respecc˜
o
tivamente pot tgh, cotgh, sech e cosech s˜o definidas por:
a
• tgh x =
senh x
ex − e−x
,
= x
cosh x
e + e−x

23. 23
• cotgh x =
• sech x =
cosh x
ex + e−x
= x
,
senh x
e − e−x
1
2
,
= x
cosh x
e + e−x

24. 24
• cosech x =
1
2
= x
senh x
e − e−x
1.5. Fun¸˜o peri´dica
ca
o
Dizemos que uma fun¸ao ´ f ´ peri´dica se existe um n´mero real T = 0 tal que
c˜ e e
o
u
f (x + T ) = f (x) para todo x ∈ D(f ).
• O n´mero T ´ chamado per´
u
e
ıodo da fun¸ao f .
c˜
• O gr´fico de uma fun¸ao peri´dica se repete a cada intervalo de comprimento |T |.
a
c˜
o
Exemplos:
1. As fun¸oes trigonom´tricas s˜o peri´dicas.
c˜
e
a
o
2. A fun¸ao constante ´ peri´dica e tem como per´
c˜
e
o
ıodo qualquer n´mero t = 0.
u

25. 25
3.
1.6. Fun¸˜o par e fun¸˜o ´
ca
ca ımpar
Dizemos que uma fun¸ao f ´ par se, para todo x no dom´
c˜
e
ınio de f , f (−x) = f (x).
Uma fun¸ao ´ ´
c˜ e ımpar se, para todo x no dom´
ınio de f , f (−x) = −f (x).
• O gr´fico de uma fun¸ao par ´ sim´trico em rela¸ao ao eixo dos y e o gr´fico de uma
a
c˜
e
e
c˜
a
fun¸ao ´
c˜ ımpar ´ sim´trico em rela¸ao a origem.
e
e
c˜ `
1.7. Fun¸˜o inversa
ca
Para falarmos de fun¸ao inversa, precisamos antes estudar os conceitos de fun¸ao
c˜
c˜
sobrejetora, fun¸ao injetora e fun¸ao bijetora.
c˜
c˜

26. 26
1.7.1. Fun¸˜o sobrejetora
ca
Defini¸˜o: Uma fun¸ao f de A em B ´ sobrejetora se, e somente se, para todo y
ca
c˜
e
pertencente a B existe um elemento x pertencente a A tal que f (x) = y.
Em s´
ımbolos:
f : A → B, ´ sobrejetora ⇔ ∀y, y ∈ B, ∃x, x ∈ A|f (x) = y.
e
Note que f : A → B ´ sobrejetora se, e somente se, Im(f ) = B.
e
Teorema: Se duas fun¸oes f de A em B e g de B em C s˜o sobrejetoras, ent˜o a fun¸ao
c˜
a
a
c˜
composta g ◦ f de A em C ´ tamb´m sobrejetora.
e
e
1.7.2. Fun¸˜o injetora
ca
Defini¸˜o: Uma fun¸ao f de A em B ´ injetora se, e somente se, quaisquer que sejam
ca
c˜
e
x1 e x2 de A, se x1 = x2 , ent˜o f (x1 ) = f (x2 ).
a
Em s´
ımbolos:
f : A → B, ´ injetora ⇒ (∀x1 , x1 ∈ A, ∀x2 , x2 ∈ A)(x1 = x2 ⇒ f (x1 ) = f (x2 )).
e
Note que esta defini¸ao ´ equivalente a: uma fun¸ao f de A em B ´ injetora se, e
c˜ e
c˜
e
somente se, quaisquer que sejam x1 e x2 de A, se f (x1 ) = f (x2 ), ent˜o x1 = x2 .
a
Em s´
ımbolos:
f : A → B, ´ injetora ⇒ (∀x1 , x1 ∈ A, ∀x2 , x2 ∈ A)(f (x1 ) = f (x2 ) ⇒ x1 = x2 ).
e

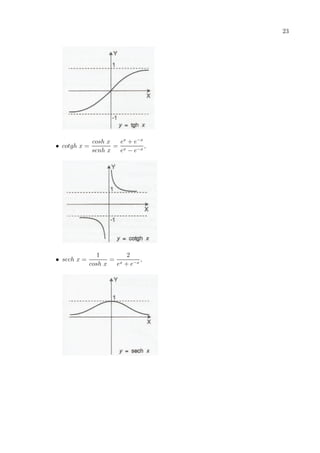
27. 27
Teorema: Se duas fun¸oes f de A em B e g de B em C s˜o injetoras, ent˜o a fun¸ao
c˜
a
a
c˜
composta g ◦ f de A em C ´ tamb´m injetora.
e
e
1.7.3. Fun¸˜o bijetora
ca
Defini¸˜o: Uma fun¸ao f de A em B ´ bijetora se, e somente se, f ´ sobrejetora e
ca
c˜
e
e
injetora.
Esta defini¸ao ´ equivalente a: uma fun¸ao f de A em B ´ bijetora se, e somente se,
c˜ e
c˜
e
para qualquer elemento y pertencente a B, existe um unico elemento x pertencente a A
´
tal que f (x) = y.
Reconhecimento atrav´s do gr´fico: Pela representa¸ao cartesiana de uma fun¸ao f
e
a
c˜
c˜
podemos verificar se f ´ injetora ou sobrejetora ou bijetora. Para isso, basta analisarmos
e
o n´mero de pontos de intersec¸ao das retas paralelas ao eixo dos x, conduzidas por cada
u
c˜
ponto (0, y) em que y ∈ B (contradom´
ınio de f ).
• se nenhuma reta corta o gr´fico mais de uma vez, ent˜o f ´ injetora.
a
a
e
• se toda reta corta o gr´fico, ent˜o f ´ sobrejetora.
a
a
e
• se toda reta corta o gr´fico em um s´ ponto, ent˜o f ´ bijetora.
a
o
a
e
Exemplos:
1. Dado a ∈ R, 0 < a = 1, as fun¸oes f : R → R∗ , onde f (x) = ax , e g : R∗ → R,
c˜
+
+
onde g(x) = loga x, s˜o inversas uma da outra.
a
2. Fun¸ao arco seno
c˜
π π
Seja f : [− , ] → [−1, 1], a fun¸ao definida por f (x) = sen x. A fun¸ao inversa
c˜
c˜
2 2
de f (x) ser´ chamada arco seno e denotada por
a
π π
f −1 : [−1, 1] → [− , ], onde f −1 (x) = arc sen x.
2 2

28. 28
Simbolicamente, para −
π
π
≤y≤ ,
2
2
y = arc sen x ⇔ sen y = x
3. Fun¸ao arco cosseno
c˜
Seja f : [0, π] → [−1, 1], a fun¸ao definida por f (x) = cos x. A fun¸ao inversa de
c˜
c˜
f (x) ser´ chamada arco cosseno e denotada por
a
f −1 : [−1, 1] → [0, π], onde f −1 (x) = arc cos x.
Simbolicamente, para 0 ≤ y ≤ π,
y = arc cos x ⇔ sen y = x
4. Fun¸ao arco tangente
c˜
A inversa da fun¸ao tangente ´ definida para todo n´mero real.
c˜
e
u
π π
c˜
c˜
Seja f : (− , ) → R, a fun¸ao definida por f (x) = tg x. A fun¸ao inversa de f (x)
2 2

29. 29
ser´ chamada arco tangente e denotada por
a
π π
f −1 : (− , ) → R, onde f −1 (x) = arc tg x.
2 2
Simbolicamente, para −
π
π
<y< ,
2
2
y = arc tg x ⇔ tg y = x
5. Outras fun¸oes trigonom´tricas inversas
c˜
e
Podemos definir a fun¸ao inversa da cotangente como
c˜
y = arc cotg x =
π
− arc tg x,
2
onde 0 < y < π.
As inversas da secante e da cossecante ser˜o fun¸oes de x no dom´ |x| ≥ 1, desde
a
c˜
ınio
que adotemos as defini¸oes:
c˜
1
y = arc sec x = arc cos ( )
x
1
y = arc cosec x = arc sen ( )
x

30. 30

31. 2. Aplica¸oes
c˜
Nas mais diversas areas utilizam-se fun¸oes para a compreens˜o de fenˆmenos e re´
c˜
a
o
solu¸ao de problemas. Formalmente podemos dizer que estamos modelando o mundo
c˜
´
ao nosso redor. E claro que essa afirma¸ao n˜o ´ completamente verdadeira, pois o
c˜
a e
mundo ao nosso redor ´ altamente complexo e ao trabalharmos com um modelo fazemos
e
simplifica¸oes para reduzir essa complexidade.
c˜
Em geral, os modelos s˜o validados para que sejam efetivamente aplic´veis como
a
a
ferramentas para entender e analisar diferentes fenˆmenos. Os exemplos apresentados
o
aqui s˜o did´ticos e, portanto, n˜o foram necessariamente validados.
a
a
a
Exemplos:
1. O pre¸o de uma corrida de taxi, em geral, ´ constitu´ de uma parte fixa, chamada
c
e
ıdo
bandeirada, e de uma parte vari´vel, que depende do n´mero de quilˆmetros rodaa
u
o
dos. Em uma cidade X a bandeirada ´ de R 10,00 e o pre¸o do quilˆmetro rodado
e
c
o
´ de R 0,50.
e
(a) Determine a fun¸ao que representa o pre¸o da corrida.
c˜
c
(b) Se algu´m pegar um taxi no centro da cidade e se deslocar para sua casa,
e
situada a 8 km de distˆncia, quanto pagar´ pela corrida?
a
a
2. Um avi˜o com 120 lugares ´ fretado para uma excurs˜o. A companhia exige de
a
e
a
cada passageiro R 900,00 mais uma taxa de R 10,00 para cada lugar vago. Qual
o n´mero de passageiros que torna m´xima a receita da companhia?
u
a

32. 32
3. Restri¸˜o orcament´ria: Em nosso pa´ um dos problemas que os governos
ca
a
ıs,
enfretam diz respeito a aloca¸ao de verbas para programas sociais e pagamento de
`
c˜
funcion´rios. Vamos supor que existe um montante fixo M, a ser repartido entre os
a
dois prop´sitos. Se denotarmos po x o montante a ser gasto com o pagamento de
o
funcion´rios e por y o montante destinado aos programas sociais, temos
a
M = x + y.
Essa equa¸ao ´ conhecida como restri¸˜o orcament´ria. Seu gr´fico ´ uma reta.
c˜ e
ca
a
a
e
Como as vari´veis x e y s˜o n˜o negativas, s´ a parte do primeiro quadrante ´ de
a
a a
o
e
interesse para a an´lise.
a
(a) Qual a leitura pr´tica que podemos fazer desse gr´fico?
a
a
(b) Suponha que numa cidade X existam 200 funcion´rios que ganham um sal´rio
a
a
m´dio de R 800,00 mensais e que o montante M ´ de R 300.000,00 mensais.
e
e
Qual o montante mensal dispon´ para programas sociais? Os funcion´rios
ıvel
a
reivindicam 13% de aumento em seus sal´rios. Qual o impacto desse aumento
a
sobre os programas sociais?

33. 33
4. Crescimento populacional: Para prever a popula¸ao de um dado pa´ numa
c˜
ıs
data futura, muitas vezes ´ usado um modelo de crescimento exponencial.
e
Para isso, observa-se o valor real da popula¸ao em intervalos de tempo iguais,
c˜
por um dado per´
ıodo de tempo. Calcula-se, a seguir, a raz˜o entre a popula¸ao
a
c˜
observada em per´
ıodos consecutivos. Se a raz˜o for aproximadamente constante,
a
em cada observa¸ao, a popula¸ao ´ dada pela popula¸ao anterior multiplicada por
c˜
c˜ e
c˜
esta raz˜o, que ´ chamada fator de crescimento.
a
e
A tabela a seguir apresenta dados da popula¸ao brasileira no per´
c˜
ıodo de 1940 a
1980.
Ano Popula¸ao absoluta
c˜
1940
41.165.289
1950
51.941.767
1960
70.070.457
1970
93.139.037
1980
119.002.706
Raz˜o
a
51.941.767 ∼
= 1, 26
41.165.289
70.070.457 ∼
= 1, 35
51.941.767
93.139.037 ∼
= 1, 33
70.070.457
119.002.706 ∼
= 1, 2
93.139.037
(a) Usando esses dados, obter uma previs˜o para a popula¸ao brasileira no ano
a
c˜
2000.
(b) Sabendo que a popula¸ao brasileira no ano 2000 era de 169.799.170, qual o
c˜
erro cometido, em percentual, na previs˜o?
a
5. Decaimento radioativo: A massa de materiais radioativos, tais como o r´dio, o
a
urˆnio ou o carbono-14, se desintegra com o passar do tempo. Uma maneira usual
a
de expressar a taxa de decaimento da massa ´ utilizando o conceito de meia-vida
e
desses materiais.
A meia-vida de um material radioativo ´ definida como o tempo necess´rio para
e
a
que sua massa seja reduzida a metade.
`
Denotamos por M0 a massa inicial (correspondente ao instante t = 0) e por M a
massa presente num instante qualquer t, podemos estimar M pela fun¸ao exponenc˜

34. 34
cial dada por
M = M0 e−kt
sendo K > 0 uma constante.
A equa¸ao acima ´ conhecida como modelo de decaimento exponencial. A constante
c˜
e
K depende do material radioativo considerado e est´ relacionada com a meia-vida
a
dela.
Sabendo que a meia-vida do carbono-14 ´ de aproximadamente 5.730 anos, detere
minar:
(a) a constante K, do modelo de decaimento exponencial para esse material;
(b) a quantidade de massa presente ap´s dois per´
o
ıodos de meia-vida, se no instante
t = 0 a massa era M0 ;
(c) a idade estimada de um organismo morto, sabendo que a presen¸a do carbonoc
14 neste ´ 80% da quantidade original.
e

35. Referˆncias
e
FLEMMING, Diva M.; GONCALVES, Mirian Buss. C´lculo A: Fun¸oes, limite, deriva¸ao
¸
a
c˜
c˜
e integra¸ao. 6 ed. S˜o Paulo: Pearson Prentice Hall, 2006.
c˜
a
Apostila de Pr´-C´lculo - Unochapec´
e a
o
IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos de Matem´tica Elementar.
a
Vol 1. S˜o Paulo: Atual, 1993.
a