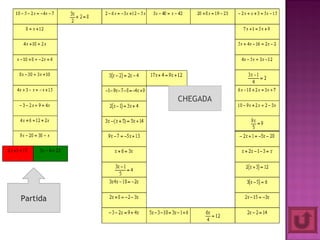
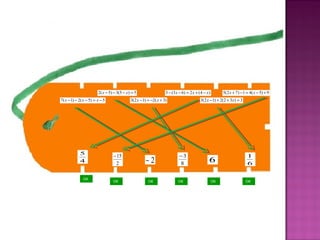
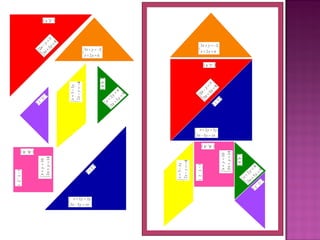
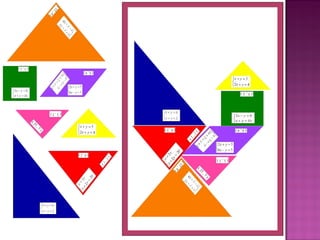
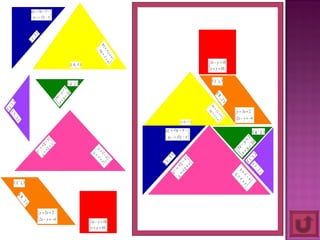
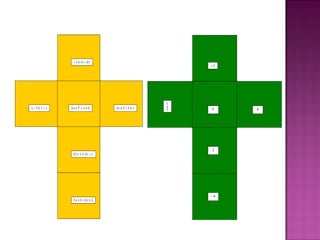
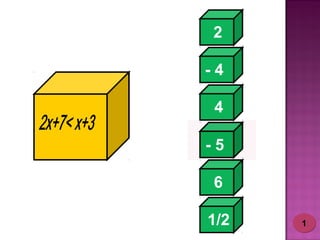
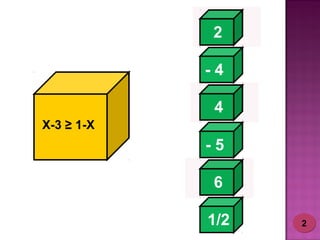
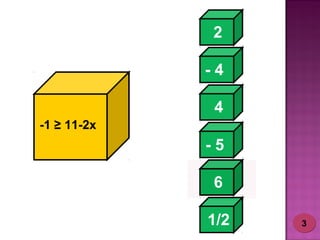
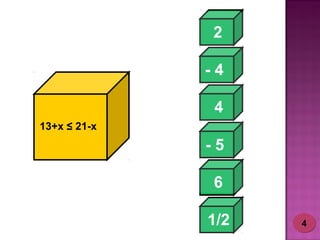
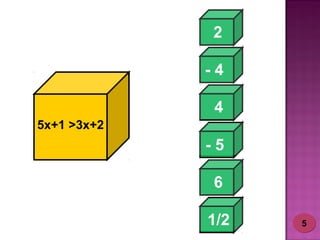
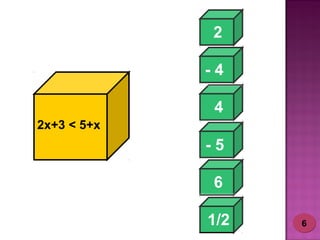
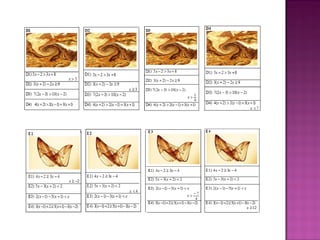
1) O documento descreve um curso de mestrado profissionalizante em ensino de física e matemática que avalia a aplicação de jogos no ensino de equações, inequações e sistemas de equações do 1o grau. 2) Foram desenvolvidos vários jogos aplicados com 24 alunos do 6o ano do ensino fundamental para ensinar esses tópicos de forma lúdica. 3) A pesquisa concluiu que os jogos melhoraram a compreensão dos alunos sobre os conteúdos ensinados.

1. CCUURRSSOO DDEE MMEESSTTRRAADDOO PPRROOFFIISSSSIIOONNAALLIIZZAANNTTEE EEMM
EENNSSIINNOO DDEE FFÍÍSSIICCAA EE DDEE MMAATTEEMMÁÁTTIICCAA
AAVVAALLIIAAÇÇÃÃOO DDAA AAPPLLIICCAAÇÇÃÃOO DDEE JJOOGGOOSS NNAA 66ª
SSÉÉRRIIEE:: EQUAÇÕES, INEQUAÇÕES E SISTEMAS DE
EQUAÇÕES DO 1º GRAU
Mestranda: Angelita Uberti
Orientadora: Profª Helena Noronha Cury
Santa Maria, Maio de 2011

2. IINNTTRROODDUUÇÇ
ÃÃOO
O presente trabalho consiste no produto de dissertação de
Mestrado Profissional, é constituído por um conjunto de
atividades (jogos), que tem por objetivo proporcionar aos colegas,
professores de Matemática, sugestão de mudança na rotina em
sala de aula, tendo em vista que representa algo de diferente
para se fazer deixando de lado práticas tradicionais de ensino,
tais como o uso de exercícios realizados apenas com lápis e
papel, despertando no aluno o interesse e o gosto de aprender as
equações, os sistemas de equação e as inequações do 1º grau
com uma incógnita.

3. O trabalho desenvolveu-se com uma turma de 6ª série do
Ensino Fundamental de uma escola municipal do interior do Rio
Grande do Sul. A partir da revisão de literatura baseada em
autores que trabalham com jogos e com álgebra, bem como da
análise de livros didáticos usados no Ensino Fundamental para o
ensino de equações, sistemas de equações e inequações,
construíram-se jogos, que foram aplicados a 24 alunos de uma 6ª
série.
A pesquisa é de caráter qualitativo e nela empregaram-se,
como instrumentos, um pré-teste e anotações de observações em
um diário de campo. Analisou-se a aplicação de cada um dos
jogos e foi possível notar que houve melhor compreensão, por
parte dos alunos, sobre os conteúdos envolvidos.

4. Considera-se que a experiência pode ser reaplicada em
outras turmas e, para isso, elaborou-se um conjunto de
atividades, em que são apresentados os jogos e sugestões
para os professores.

5. JJOOGGOOSS
TRILHA DAS EQUAÇÕES
VIRA E CONFERE
QUEBRA - CABEÇA
É OU NÃO É SOLUÇÃO
QUARTETO DAS INEQUAÇÕES
Sair

7. Conteúdo Desenvolvido:
Resolução de Equações do 1º Grau com uma Incógnita
1.Objetivo.
- Observar e listar as dificuldades apresentadas pelos alunos.
- Exercitar os conhecimentos adquiridos sobre a resolução de
equações do 1º grau com uma incógnita.
- Desenvolver habilidades de raciocínio.
2. Carga Horária: 3 (três) horas – aula.
3. Metodologia:
Aulas expositivas e dialogadas

8. 4. Material necessário para confecção do jogo:
- Um tabuleiro.
- Duas tampas de creme dental (para servirem como peões)
Objetivo do jogo:
Chegar em primeiro lugar ao espaço com a palavra CCHHEEGGAADDAA.
Regras:
O jogo consiste em percorrer o caminho (trilha), que é composta
de retângulos, nos quais estão escritas equações.

9. - O aluno deve resolver as equações e a solução encontrada é
o número de casas que ele deve percorrer; se a solução for um
número positivo, o aluno irá avançar este número de casas, caso a
solução seja um número negativo, o aluno terá que voltar esse o
número de casas.
- Dois alunos jogam alternadamente.
- Vence o aluno que chegar em primeiro lugar ao
espaço com a palavra CCHHEEGGAADDAA.

10. Partida
CHEGADA

12. Conteúdo Desenvolvido:
Resolução de Equações do 1º Grau com uma Incógnita
envolvendo parênteses.
1. Objetivo.
- Observar e listar as dificuldades apresentadas pelos alunos.
- Aplicar os conhecimentos adquiridos sobre a resolução de
equações do 1º grau com uma incógnita envolvendo
parênteses.
- Promover o trabalho em equipe.
2. Carga Horária: 2 (duas) horas – aula.

13. 3. Metodologia:
Aulas expositivas e dialogadas
Jogo “Vira e Confere”
O Vira e Confere consiste em uma cartela, em material rígido,
em cuja ponta é inserido um barbante com um nó. Na cartela há
seis equações do 1º grau com suas respectivas respostas, sendo
que estas não aparecem na mesma ordem em que as equações.
Material necessário para confecção:
Folha de isopor
EVA
Fita ou barbante

14. Regras
Cada aluno deve pegar uma cartela, passar a fita sobre a
primeira ranhura em cima, à esquerda, abaixo da qual há uma
equação; em seguida, encontra a solução correspondente a essa
equação, na parte inferior da cartela, e passa a fita por cima, até
a ranhura correspondente à resposta; após, passa a fita por baixo
da cartela até a segunda ranhura e continua o processo até a
última, depositando a fita na ranhura central à direita.Vira, então,
a cartela e confere o desenho determinado pela fita. Se coincidir
com o da cartela, o aluno acertou todas as questões, caso
contrário pode tentar novamente.

15. 2(x -5) -3(5 - x) = 5
7(x -1) - 2(x -5) = x -5
3-(3x -6) = 2x +(4 - x)
3(2x -1) = -2(x +3)
5(2x + 7) -1 = 4(x -5) +9
3(2x -1) + 2(2 +3x) = 3
5
4
-15 2
- 2 8
-3 6 1
6
OK OK OK OK
OK
OK

19. Conteúdo Desenvolvido:
Resolução de Sistemas de Equações do 1º Grau com uma
Incógnita / Método da Substituição.
1. Objetivo.
- Observar e listar as dificuldades apresentadas pelos alunos.
-Aplicar os conhecimentos adquiridos sobre a resolução de
sistemas de equações do 1º grau com uma incógnita utilizando o
método da substituição.
2. Carga Horária: 2 (duas) horas – aula.

20. 3. Metodologia:
Aulas expositivas e dialogadas.
Jogo “Quebra-cabeça”
O jogo consiste em montar figuras com o auxilio das sete peças
de um tangram, estas podem ser de uma cor só ou de várias cores,
nelas estão indicados sistemas de equações e suas possíveis
soluções.
Material necessário para confecção do jogo:
Papel cartão para a confecção do tangram

21. Objetivo:
Montar figuras em que há sistemas de equações do 1º grau
com uma incógnita e suas soluções.
Regras:
O aluno deve resolver cada sistema e, encontrada a solução,
deve clicar sobre a peça que tem a solução do sistema, que ficará
adjacente à outra em que há o sistema correspondente.

23. Conteúdo Desenvolvido:
Resolução de Sistemas de Equações do 1º Grau com uma
Incógnita / Método da Comparação.
1. Objetivo.
Observar e listar as dificuldades apresentadas pelos alunos.
Fixar a resolução de sistemas de equações do 1º grau com
uma incógnita utilizando o método da comparação.
2. Carga Horária: 2 (duas) horas – aula.

25. Conteúdo Desenvolvido:
Resolução de Sistemas de Equações do 1º Grau com uma
Incógnita / Método da Adição.
1. Objetivo.
Observar e listar as dificuldades apresentadas pelos alunos.
Exercitar a resolução de sistemas de equações do 1º grau
com uma incógnita utilizando o método da adição.
2. Carga Horária: 2 (duas) horas – aula.

28. Conteúdo Desenvolvido:
Resolução de Inequações do 1º Grau com uma Incógnita.
1. Objetivo.
- Observar e listar as dificuldades apresentadas pelos alunos.
- Desenvolver habilidades de raciocínio
2. Carga Horária: 2 (duas) horas – aula.
3. Metodologia:
- Aulas expositivas e dialogadas.

29. Material necessário para confecção do jogo:
- Dois dados confeccionados em papel cartão, como o
modelo.
Objetivo do jogo:
- Vencer o maior número de rodadas.
Regras:
- É jogado por dois alunos.
- As jogadas são alternadas.

30. - Cada aluno, na sua vez, lança os dados e verifica se o
número que saiu no dado da esquerda é solução da inequação
que aparece no dado da direita.
-Se o aluno encontrar a solução da inequação, este marca
dois pontos positivos, porém se o número encontrado não for
solução da inequação, então o aluno marca um ponto negativo.
- Vence o jogo quem marcar mais pontos positivos ao final de
seis rodadas.

32. 2
- 4
4
- 5
6
1/2
11

33. 2
- 4
4
- 5
6
1/2
X-3 ≥ 1-X
22

34. 2
- 4
4
- 5
6
1/2
-1 ≥ 11-2x
33

35. 2
- 4
4
- 5
6
1/2
13+x ≤ 21-x
44

36. 2
- 4
4
- 5
6
1/2
- 4
5x+1 >3x+2
55

37. 2
- 4
4
- 5
6
1/2
- 4
2x+3 < 5+x
66

38. Tente
novamente

39. OK
Continuar

40. OK
Continuar

41. Continuar
OK

42. Continuar
OK

43. Continuar
OK

44. Menu
OK

46. Conteúdo Desenvolvido:
Resolução de Inequações do 1º Grau com uma Incógnita.
1.Objetivo.
Observar e listar as dificuldades apresentadas pelos alunos.
Exercitar os conhecimentos adquiridos sobre a resolução de
inequações do 1º grau com uma incógnita.
Desenvolver habilidades de raciocínio.
2. Carga Horária: 2 (duas) horas – aula.

47. 3. Metodologia:
Aulas expositivas e dialogadas
Jogo “Quarteto das Inequações”
Neste jogo, os alunos recebem o baralho de 36 cartas,
constituídos de nove quartetos. Em cada quarteto, há quatro
inequações, uma das inequações já com a solução e as outras
três em aberto. As cartas são embaralhadas e distribuídas para
três ou quatro jogadores. Se algum jogador notar que já tem um
quarteto formado, deve colocar ao lado.

48. Para ilustrar a frente das cartas, foram usadas figuras que
representam fractais.
Material:
Os materiais utilizados para a confecção do baralho
- folhas de papel cartão;
- folhas de oficio;
- papel contac;
Objetivo:
Conseguir o maior número de quartetos possíveis.

49. Para ilustrar a frente das cartas, foram
usadas figuras que representam fractais.
Material:
Os materiais utilizados para a confecção
do baralho
- folhas de papel cartão;
- folhas de oficio;
- papel contac;
Objetivo:
Conseguir o maior número de quartetos
possíveis.

50. Reg
- Cada grupo recebe um baralho com 36 cartas, constituídos
ras:
de nove quartetos.
- Escolhe-se um jogador para iniciar o jogo. Este tem, por
exemplo, a carta A1; pergunta aos colegas quem tem a carta A2.
Se um colega se manifesta afirmativamente, então o que fez a
pergunta deve responder corretamente à questão proposta na
carta A2 e o outro deve lhe entregar esta carta; ele continua
perguntando, para qualquer colega do jogo, pelas outras cartas
que lhe faltam, do quarteto A.

51. - Quando errar a resposta, o colega a quem ele perguntou
continuará o jogo, da mesma forma.
- O jogo termina quando todos os quartetos forem formados.