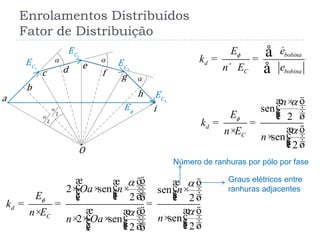
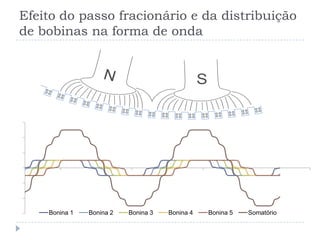
1) O documento descreve os fundamentos das máquinas elétricas rotativas de corrente alternada, incluindo a conversão de energia mecânica em elétrica e vice-versa.
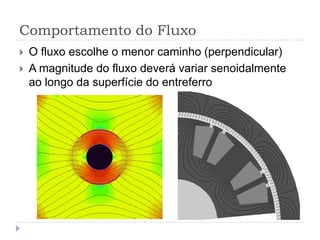
2) É explicado como a tensão é induzida em uma espira em um campo magnético uniforme, dependendo do fluxo magnético, da velocidade de rotação e de constantes geométricas.
3) O torque induzido em uma máquina síncrona também depende do campo magnético do estator e rotor, do ângulo entre


![Tensão Induzida [1]
( )
( )
ind
ind sin ab
e
l
v B l
e v B
= ´
= × ××](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-4-320.jpg)
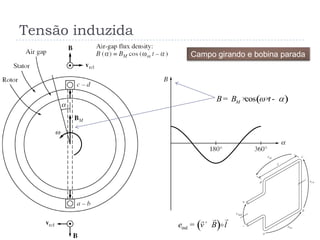
![1. Segmento ab
2. Segmento bc
3. Segmento cd
4. Segmento da
Resultante
Tensão Induzida [2]
( )senba abe v B l = × ××
0bce =
( )sendc dce v B l = × × ×
0dae =
( )tot 2 sene v B l = × × × ×](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-5-320.jpg)
![Tensão Induzida [3]
A tensão induzida depende de três fatores:
1. Fluxo da máquina, f
2. Velocidade de rotação, w
3. Constante que depende da construção da máquina, k
( )
( )
ind
max
ind max
2 sen
sen
t
v r
e r B l t
A B
e t
w
w
w w
f
f w w
= ×
= ×
= × × × × × ×
= ×
= × × ×](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-6-320.jpg)
![Torque Induzido [1]
( )F i l B= × ´
r F
= ´](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-7-320.jpg)
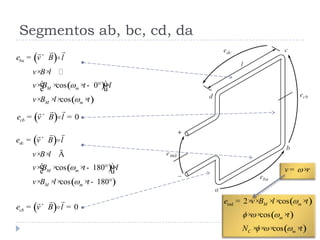
![1. Segmento ab
2. Segmento bc
3. Segmento cd
4. Segmento da
Resultante
Torque Induzido [2]
( )senba abr i l B = ×× × ×
0bc =
( )sencd cdr i l B = ×× × ×
0da =
( )total 2 senr i l B = × ×× × ×](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-8-320.jpg)
![( )
( )
( )
ind
loop
ind loop
ind
2
ind loop
2 sen
sen
sen
S
S
r l
i
S
r i l B
G B
A B
B
A G
B
k
B
B
××
= × × × × ×
×
=
×
=
=
× ×
×
×
´
× × ×
Torque Induzido [3]
loop
i
B
G
×
=
Constante que
depende da
geometria do loop
Para um círculo 2G r= ×](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-9-320.jpg)
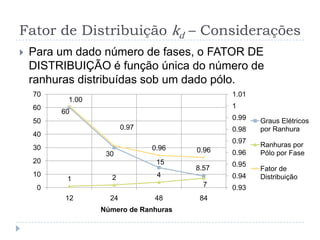
![Torque Induzido [4]
O torque induzido depende de quatro fatores:
1. Intensidade do campo magnético do rotor
2. Intensidade do campo magnético do estator
3. Seno do ângulo entre os campos magnéticos
4. Constante que depende da construção da máquina
( )ind loop Sk B B = × ´
](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-10-320.jpg)

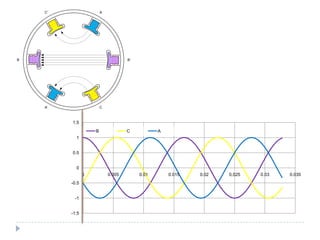
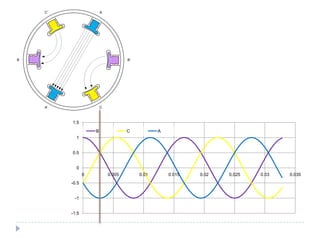
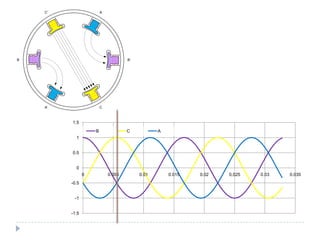
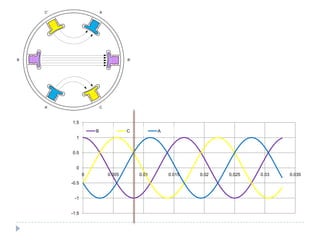
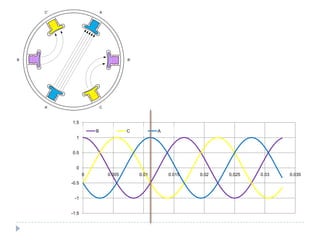
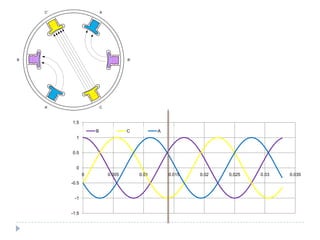
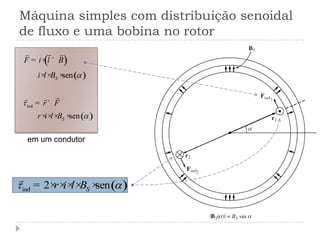
![O campo magnético girante [1]
Dois campos magnéticos tendem a se alinhar
Se um deles for girante o outro tentará perseguí-lo
Correntes defasadas de 120º
( ) ( )
( ) ( )
( ) ( )
'
'
'
sen 0 A
sen 120 A
sen 240 A
aa M
bb M
cc M
i t I t
i t I t
i t I t
w
w
w
= × × - °
= × × - °
= × × - °](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-12-320.jpg)
![O campo magnético girante [1]
Dois campos magnéticos tendem a se alinhar
Se um deles for girante o outro tentará perseguí-lo
Correntes defasadas de 120º
( ) ( )
( ) ( )
( ) ( )
'
'
'
sen 0 A
sen 120 A
sen 240 A
aa M
bb M
cc M
i t I t
i t I t
i t I t
w
w
w
= × × - °
= × × - °
= × × - °](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-13-320.jpg)
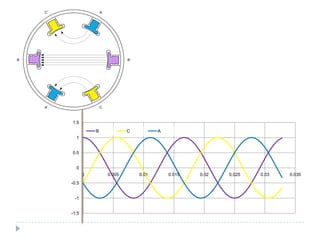
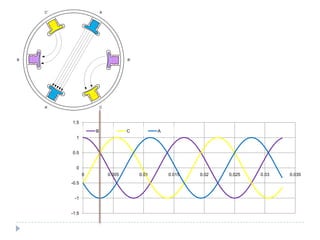
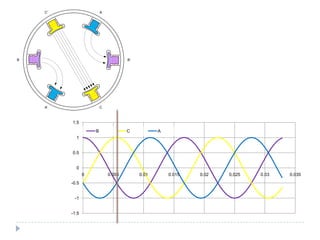
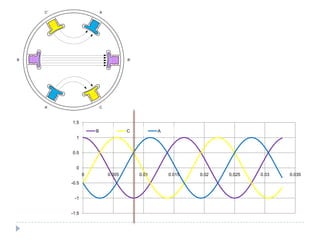
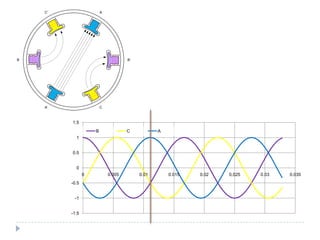
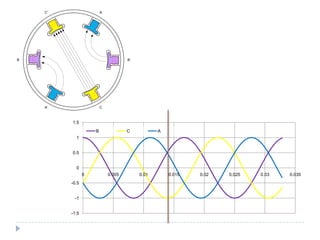
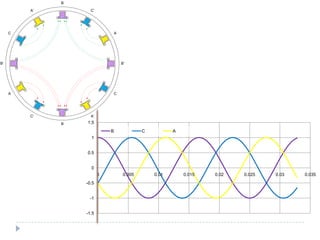
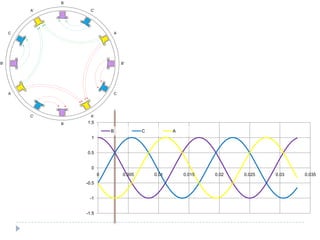
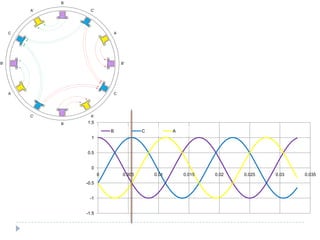
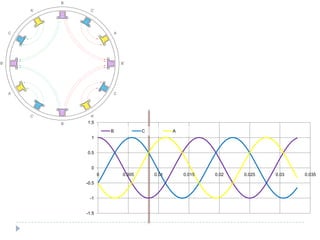
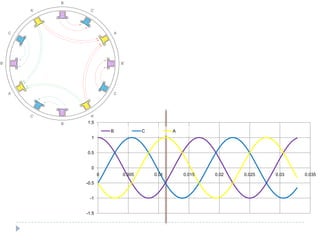
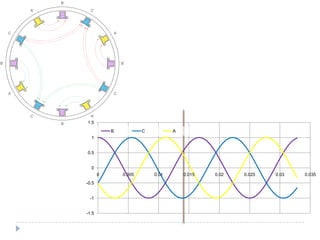
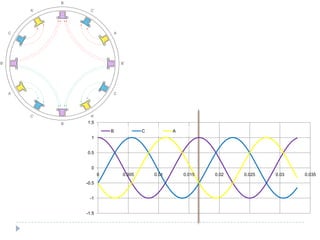
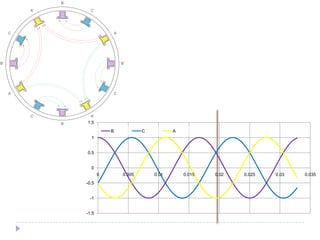
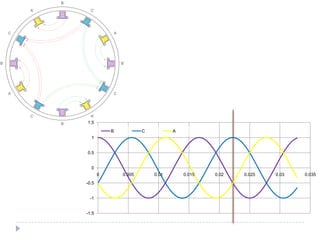
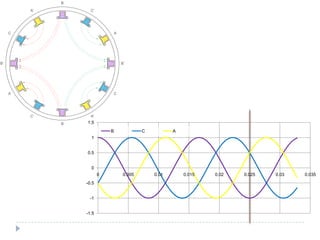
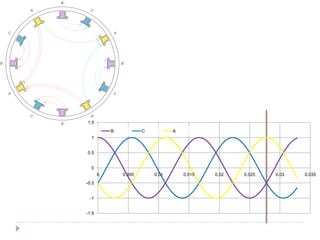
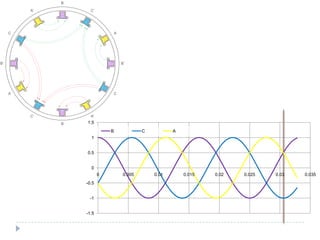
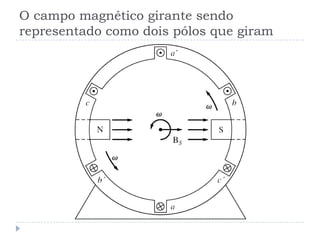
![Com 4 pólos [1]](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-39-320.jpg)
![Com 4 pólos [2]](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-40-320.jpg)


![clear all;
close all;
clc;
% Parametrizando as codições básicas
bmax = 1; % Normalizando bmax para 1
freq = 60; % 60 Hz
w = 2*pi*freq; % freqüência angular (rad/s)
% Primeiro, gere os três componentes do campo
magnético
t = 0:1/6000:5.2/60;
Baa = sin(w*t) .* (cos(0) + j*sin(0));
Bbb = sin(w*t-2*pi/3) .* (cos(2*pi/3) + j*sin(2*pi/3));
Bcc = sin(w*t+2*pi/3) .* (cos(-2*pi/3) + j*sin(-2*pi/3));
% Calculando o Bresultante
Bresultante = Baa + Bbb + Bcc;
% Calculando um círculo que representa o máximo
% valor estimadod para Bresultante
circle = 1.5 * (cos(w*t) + j*sin(w*t));
% Plote a magnitude e a direção dos campos
magnéticos
% resultantes. Note que Baa e perto, Bbb é azul, Bcc
é
% magenta and Bresultante is vermelho
for ii = 1:length(t)
% Plot the reference circle
plot(circle,'k');
hold on
% Plote os quatro campos magnéticos
plot([0 real(Baa(ii))],[0
imag(Baa(ii))],'k','LineWidth',2);
plot([0 real(Bbb(ii))],[0
imag(Bbb(ii))],'b','LineWidth',2);
plot([0 real(Bcc(ii))],[0
imag(Bcc(ii))],'m','LineWidth',2);
plot([0 real(Bresultante(ii))],[0
imag(Bresultante(ii))],'r','LineWidth',3);
axis square;
axis([-2 2 -2 2]);
drawnow;
hold off
end](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-43-320.jpg)

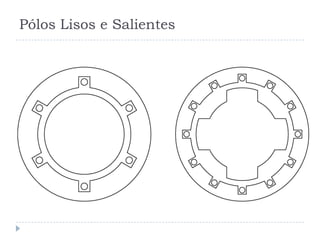





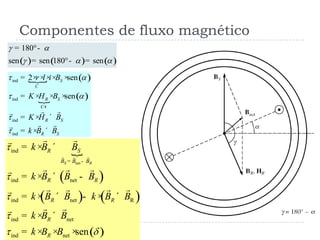






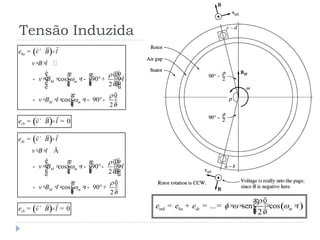
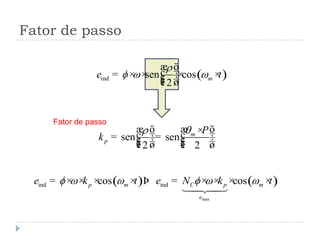
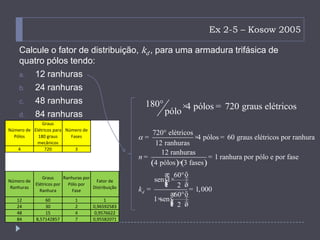
![Tensões em enrolamentos de
passo pleno e de passo fracionário [Kosow 2005]
1 1
2 bobinas
soma fasorial nos dois lados da bobina
soma aritmética nos dois lados da bobina 2
C C
p p
C
E E
k k
E n E
= = Þ =
× ×
1
E
2
E
C
E
1
cos
2
E
2
cos sen
2 2
pk
æ ö æ ö÷ ÷ç ç= =÷ ÷ç ç÷ ÷ç çè ø è ø
180 = +](https://image.slidesharecdn.com/acmachineryfundamentals-130611141354-phpapp02/85/Ac-machinery-fundamentals-70-320.jpg)