O documento introduz conceitos básicos sobre máquinas elétricas, incluindo exemplos comuns, razões para sua prevalência, unidades e notações, movimento rotativo, campo magnético, comportamento magnético de materiais ferromagnéticos, princípios de indução e força em máquinas elétricas. Exemplos e exercícios ilustram esses conceitos.



![Movimento Rotativo, Leis de Newton e
Relações de Potência [1]
2 2
2 2
x
dx d
v
dt dt
dv d x d d
a
dt dt dt dt
Movimento em
torno de um EIXO](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-5-320.jpg)
![Movimento Rotativo, Leis de Newton e
Relações de Potência [3]
sin
r F
F r
F
r
](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-6-320.jpg)
![Movimento Rotativo, Leis de Newton e
Relações de Potência [2]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-7-320.jpg)
![Movimento Rotativo, Leis de Newton e
Relações de Potência [4]
F m a J
W F dx W d
d F dx d ddW dW
P F v P
dt dt dt dt
](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-8-320.jpg)
![O Campo Magnético [1]
1. Um condutor pelo qual circula uma corrente
produz um campo magnético ao seu redor
2. Um campo magnético variante com o tempo induz
uma tensão sobre uma bobina
3. Um condutor pelo qual circula uma
corrente, imerso em um campo magnético, sofre
ação de uma força
4. Um condutor em movimento imerso em um campo
magnético sofre uma tensão induzida](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-10-320.jpg)
![O Campo Magnético [2]
Lei de Ampère
netH dl I
Supondo que não
há perdas de
campo
magnético, este é o
caminho fechado da
integração!
H l N I
Vetor Intensidade
de Campo
Magnético
Corrente Resultante](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-11-320.jpg)
![O Campo Magnético [3]
H esforço
estabelecido pela
corrente a fim de criar
o campo magnético
B concentração das
linhas de campo
magnético
m permeabilidade
magnética
f linhas de campo
magnético
c
N I
H
l
×
=
B Hm
= ×
A
c
B dA
B A
N I A
l
f
f
m
f
^
=
= ×
× × ×
=
ò](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-12-320.jpg)
![O Campo Magnético [4]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-13-320.jpg)
![O Campo Magnético [5]
cl
Am
 =
×
Área da
secção
transversal
nas curvas
m variável com f
mFe 2000~6000 mar
perdas de fluxo no ar
Efeito Franja](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-14-320.jpg)
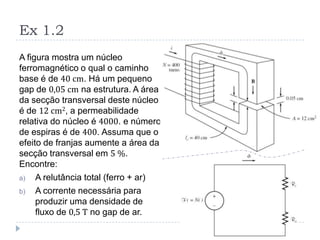
![Comportamento Magnético dos Materiais
Ferromagnéticos [1]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-18-320.jpg)
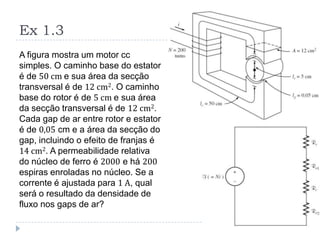
![Comportamento Magnético dos Materiais
Ferromagnéticos [2]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-19-320.jpg)
![Comportamento Magnético dos Materiais
Ferromagnéticos [3]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-20-320.jpg)
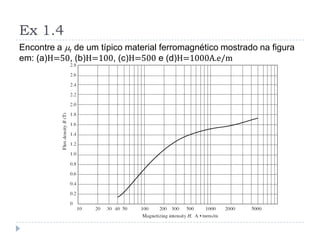

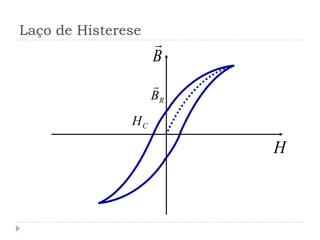
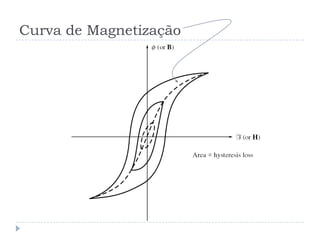
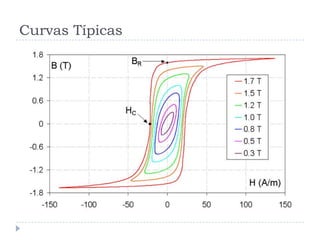
![Perdas por Histerese [1]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-23-320.jpg)
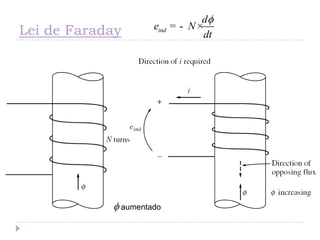
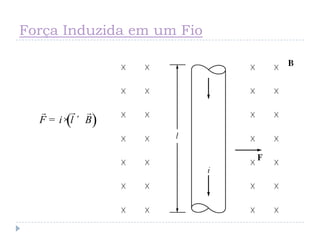
![Tensão Induzida Condutor Movimento em
um Campo Magnético [1]
( )inde v B l= ´
](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-30-320.jpg)
![Tensão Induzida Condutor Movimento em
um Campo Magnético [2]
( )inde v B l= ´
](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-31-320.jpg)
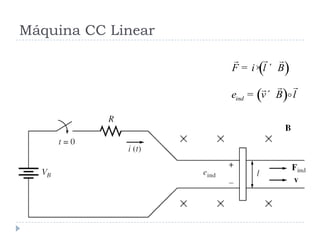
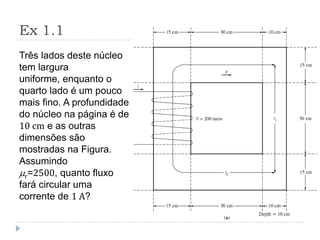
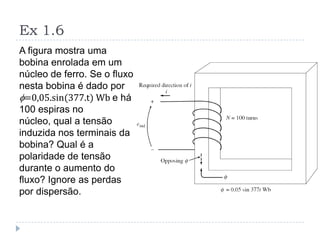
![Ex 1.10 (problemas na partida) [1]
A máquina linear mostrada na figura tem uma bateria com tensão de 120
V, uma resistência interna de 0,3 W e uma densidade de fluxo magnético de 0,1
T.
a. Qual a máxima corrente de partida? Qual a velocidade de estado
estacionário?
b. Suponha que 30 N sejam aplicados forçando para a direita a barra. Qual a
nova velocidade de estado estacionário? Quanta potência a barra está
consumindo / fornecendo? Quanta potência a bateria está fornecendo /
consumindo?
c. Suponha 30 N sejam aplicados forçando a barra para a esquerda...
d. Construa um gráfico Velocidade versus Força com a barra movimentando-
se para a direita.
e. Assuma que a barra está descarregada e que repentinamente ela desliza
em uma região onde o campo magnético é reduzido para 0,08. Quão
rapidamente a barra estará deslizado?](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-35-320.jpg)
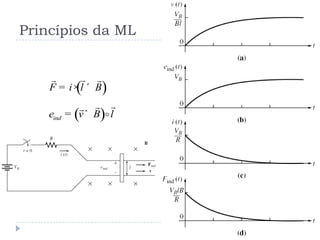
![Ex 1.10 [3]
( )inde v B l= ´
( )F i l B= × ´
](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-36-320.jpg)
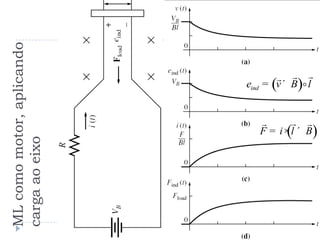
![Ex 1.10 (Velocidade X Força) [3]](https://image.slidesharecdn.com/introduction-20to-20machinery-20principles-130819114846-phpapp02/85/Introduction-to-machinery-principles-37-320.jpg)