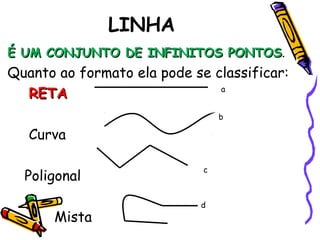
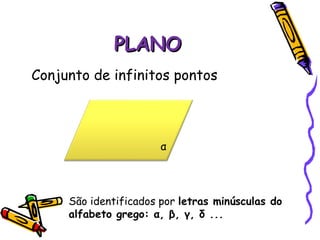
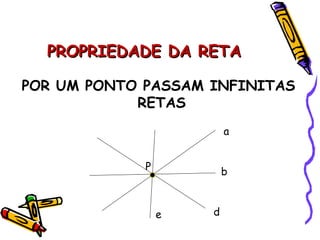
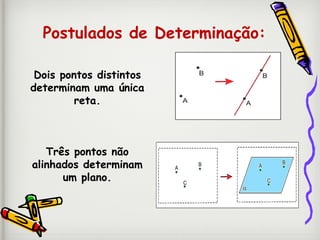
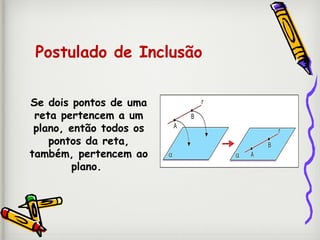
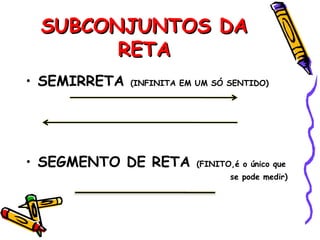
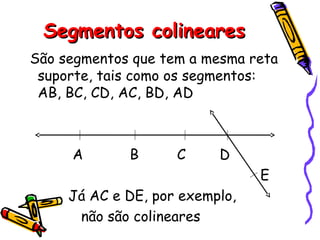
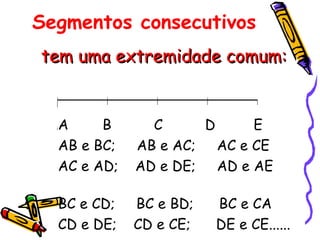
Este documento descreve conceitos básicos de geometria plana, incluindo pontos, retas, planos e suas propriedades. Define pontos como entidades sem dimensão, retas como conjuntos infinitos de pontos e planos como conjuntos infinitos de pontos. Explora propriedades como vários pontos determinarem retas e planos, e que por um ponto passam infinitas retas.

1. ElementosElementos
fundamentais dafundamentais da
GeometriaGeometria

2. Ponto, reta e plano.
Euclides
Professor da Universidade de Alexandria, autor da obra de treze
volumes: ELEMENTOS com mais de mil edições;
Método Axiomático ou dedutivo
Algumas ideias e propriedades elementares, aceitas
naturalmente, as quais servem de base a toda construção
seguinte. Definindo novos termos a partir das preexistentes, e
justificando (deduzindo) TODAS as propriedades não
elementares.

3. PONTO
Não possui formato nem dimensão.Não possui formato nem dimensão.
Pode ter duas representações :
C Pela intersecção de dois traços
.
. Com um simples toque de um lápis
B
A
Pontos são identificados por letras latinas MAIÚSCULAS.

4. LINHA
É UM CONJUNTO DE INFINITOS PONTOSÉ UM CONJUNTO DE INFINITOS PONTOS.
Quanto ao formato ela pode se classificar:
RETARETA
Curva
Poligonal
Mista
a
b
c
d

5. Estacionamento para
bicicletas

6. RETARETA
Possui uma única direção, sendo
infinita nos dois sentidos dessa
direção.
r
RetaReta pode ser identificada por letras
minúsculas do nosso alfabeto.

7. PLANOPLANO
Conjunto de infinitos pontos
α
São identificados por letras minúsculas do
alfabeto grego: α, β, γ, δ ...

8. PROPRIEDADE DA RETAPROPRIEDADE DA RETA
POR UM PONTO PASSAM INFINITAS
RETAS
a
b
de
P

9. Postulados de Existência:
Numa reta, bem como
fora dela, há infinitos
pontos.
Num plano, ou fora dele, há
infinitos pontos.

10. Postulados de Determinação:
Dois pontos distintos
determinam uma única
reta.
Três pontos não
alinhados determinam
um plano.

11. Postulado de Inclusão
Se dois pontos de uma
reta pertencem a um
plano, então todos os
pontos da reta,
também, pertencem ao
plano.

12. • Figura é qualquer
conjunto de
pontos.
• Figura plana é
uma figura que
tem todos seus
pontos num
mesmo plano.
• A Geometria
plana estuda as
figuras planas.

13. SUBCONJUNTOS DASUBCONJUNTOS DA
RETARETA
• SEMIRRETA (INFINITA EM UM SÓ SENTIDO)
• SEGMENTO DE RETA (FINITO,é o único que
se pode medir)

14. Segmentos colinearesSegmentos colineares
São segmentos que tem a mesma reta
suporte, tais como os segmentos:
AB, BC, CD, AC, BD, AD
A B C D
E
Já AC e DE, por exemplo,
não são colineares

15. Segmentos consecutivos
tem uma extremidade comum:tem uma extremidade comum:
A B C D E
AB e BC; AB e AC; AC e CE
AC e AD; AD e DE; AD e AE
BC e CD; BC e BD; BC e CA
CD e DE; CD e CE; DE e CE......

16. Segmentos adjacentesSegmentos adjacentes
São consecutivos mas nãoSão consecutivos mas não
possuem pontos internos comunspossuem pontos internos comuns
A B C D E
AB e BC; AD e DE; AC e CE
AC e AD; AB e AC; AD e AE
BC e CD; BC e AB; BC e CE
CD e DA; CD e CE; DE e CE......

17. A todo segmento de reta (não-nulo) associa-se um
número real positivo, denominado medida
(ou comprimento).
Medida de um segmento

18. Segmentos congruentesSegmentos congruentes
São segmentos de mesma medida :
LS Ξ RU
L 7cm S
R 70mm U

19. PONTO MÉDIOPONTO MÉDIO
Divide o segmento em dois segmentos
adjacentes e congruentes:
A M B

20. Referências:
•IEZZI, Gelson; MACHADO,
Antonio; DOLCE, Osvaldo.
Geometria Plana-Conceitos
básicos. 1ª edição. São Paulo:
Atual, 2008.
• DANTE, Luiz Roberto.
Matemática. Ensino Médio.
Projeto Múltiplo. São Paulo:
Ática: 2014.
•DOLCE, Osvaldo. Fundamentos de
Matemática elementar 9:
geometria plana. 8ª ed. São
Paulo: Atual, 2005.
•GIOVANNI, José Rui; PARENTE,
Eduardo. Aprendendo Matemática.
São Paulo: FTD, 2007

21. Exercícios do livro pgs 7 e 8