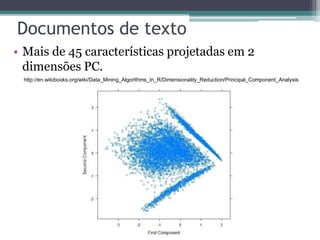
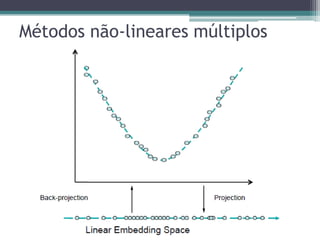
O documento discute técnicas para lidar com dados de alta dimensionalidade, incluindo redução de dimensionalidade linear como PCA e não-linear como Isomap. Exemplos demonstram como PCA pode ser usado para reduzir a dimensionalidade de imagens de rostos e documentos de texto, preservando a maior parte da variância. Métodos não-lineares são necessários quando os dados não são linearmente separáveis.

1. High Dimensional Data
Harvard Extension School
CSCI E-109 - Data Science, Lecture 8
Regis Pires Magalhães
regismagalhaes@ufc.br

2. Apresentação baseada na aula 8 de:
• Harvard Extension School
CSCI E-109 - Data Science
High Dimensional Data
http://www.cs109.org/
http://cm.dce.harvard.edu/2014/01/14328/publicationListin
g.shtml

3. Taxonomia
• Baseada no número de atributos
▫ 1 - univariate
▫ 2 - bivariate
▫ 3 - trivariate
▫ >3 – multi-variate ou high-dimensional

4. Multivariate plots

5. Multivariate plots
spawning per recruit (SPR)
yield per recruit (YPR)
Fisheries production (YPR)
Stock reproduction (SPR)

6. Scatterplot Matrix (SPLOM)
4 dimensões comparadas entre si.
Permite visualizar padrões: correlações (positivas, negativas).
ozone
ozone
radiation
radiation
temperature
temperature
wind
wind

7. SPLOM

8. Scatterplot Matrix (SPLOM)
Facilita a visualização
de correlações entre as
variáveis.

9. Geralmente não usar (3D)

10. Usar eventualmente – 3D Surface Plots

11. Lattice / Trellis Plots
Variáveis plotadas no mesmo quadro de coordenadas.

12. Lattice / Trellis Plots
Variáveis plotadas no mesmo quadro de coordenadas.

13. Lattice / Trellis Plots

14. Lattice / Trellis Plots

15. Small Multiples

16. Small multiples

17. Small multiples

18. Enroute

19. Heatmap

20. Heatmap

21. Hierarchical Heatmap

22. Coordenadas paralelas
“Hyperdimensional Data Analysis Using Parallel
Coordinates”, Wegman, 1990
Based on slide from Munzner

23. Parallel Coordinates

26. Correlação
“Hyperdimensional Data Analysis Using Parallel
Coordinates”, Wegman, 1990
Based on slide from Munzner

29. Filtragem

30. Filtering & Brushing
http://exposedata.com/parallel/

31. Conjuntos paralelos

32. StratomeX – Parallel Set

33. Bump Charts /Slope Graphs
Times de baseball
http://fathom.info/salaryper/

34. Glifos
• Glifo em tipografia, é uma figura que dá um tipo de
característica particular a um símbolo específico.
• Glifos vem da palavra grega que significa inscrição.
• Em termos de visualização de dados:
▫ Formas que codificam linhas de dados.

35. Gráficos estrela
• Variáveis ao redor de um
círculo.
• Codificação de valores em
“raios”
• Ponto de dado é agora
uma forma.

38. Gráfico em barra:
Mais eficiente e dá mais informação.

43. Redução de dimensionalidade
• Bem básico: filtragem
▫ Deixar de lado algumas dimensões.

44. O que fazer com dados de muito alta
dimensionalidade?

45. Aumento da dimensionalidade
• Quando a dimensionalidade aumenta, o volume do
espaço aumenta, de modo que os dados disponíveis
se tornam esparsos.
• O tamanho da amostra N cresce exponencialmente
com d.

46. Ideia básica
• Projetar o dado de alta dimensionalidade em um
subespaço de menor dimensão, usando
transformações lineares ou não-lineares.

47. Métodos lineares
• Colocar os dados em um hiperplano para reduzir
sua dimensionalidade.
• Aproximação para uma menor dimensão.

48. Principal Components Analysis (PCA)

49. Exemplo
a(i): Projeção de x(i) em v
v: escolhido para minimizar a
variância residual.
Encontrar v que mais se
aproxima da reconstrução de x.
Equivalente: v é a direção de
máxima variância.

50. PCA
• Projetar dados para um subespaço para maximizar a
variância dos dados projetados.
Vetores de PC são
ortogonais

51. Regressão Linear x PCA
http://stats.stackexchange.com/questions/2691/making-sense-of-principal-component-analysis-eigenvectors-eigenvalues

52. Algoritmo PCA
• Subtrair a média dos dados (centralizar X)
• Escalar cada dimensão por sua variância
▫ Para ajudar a dar menos atenção à magnitude das
dimensões.
• Calcular a matriz de covariância S.
• Calcular os k maiores autovetores de S
▫ Calculando a matriz de covariância S pode levar a
perda de precisão.
▫ Assim, não é a melhor forma de calcular
componentes principais.

53. Singular Value Decomposition (SVD)
Funciona para qualquer matriz.

54. Redução de dimensionalidade

55. Redução de dimensionalidade
Hastie et al.,”The Elements of Statistical Learning: Data Mining, Inference, and Prediction”,Springer (2009)

56. PCA para dígitos manuscritos
Hastie et al.,”The Elements of Statistical Learning: Data Mining, Inference, and Prediction”,Springer (2009)

57. PCA para dígitos manuscritos

58. PCA para imagens de faces

59. PCA para imagens de faces
64x64 imagens de faces = 4096 dados dimensionais

60. Autofaces
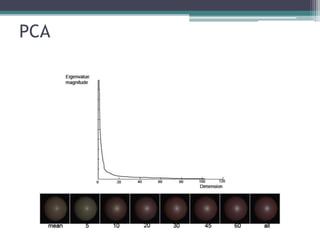
• Podemos reconstruir cada face como uma combinação linear
“faces” base ou autofaces [M. Turk and A. Pentland (1991)].
Face média
Autofaces

61. Reconstrução
• 90% da variância é capturada pelos primeiros 50
autovetores.

62. Documentos de texto
• Mais de 45 características projetadas em 2
dimensões PC.
http://en.wikibooks.org/wiki/Data_Mining_Algorithms_In_R/Dimensionality_Reduction/Principal_Component_Analysis

63. Funções de distribuição de refletividadade
bi-direcionais
• Bi-Directional Reflectance Distribution Functions (BRDFs)
• Funções que dizem quanta luz é refletida em cada direção.

64. BRDFs orientados a dados
• Medir luz refletida em uma esfera.
• 20-80 milhões de medidas (6000 imagens) por
material (cerca de 200 materiais).

65. BRDFs orientados a dados
• Cada BRDF tabulado é um vetor em um espaço
dimensional 90 x 90 x 180x3 =4,374,000
• 200 materiais

66. PCA

67. Interpolação PCA

68. Interpolação PCA com resultado estranho

69. Por que modelos lineares falham?

70. Por que modelos lineares falham?
• Exemplo clássico: “Torta suíça”

71. Métodos não-lineares múltiplos

72. Métodos não-lineares múltiplos
• Intuição: distorção em áreas locais, mas fiel em
relação à estrutura global.

73. Modelo BRDF Não-Linear
• Espaço 15-dimensional (ao invés de 45 PCs)
• Mais robusto (permite extrapolações)

74. Redução de dimensionalidade
• Métodos lineares
▫ Principal Component Analysis (PCA) – Hotelling
▫ Singular Value Decomposition (SVD) –
Eckart/Young
▫ Multidimensional Scaling (MDS) – Young
• Métodos não-lineares
▫ IsoMap – Tenenbaum
▫ Locally Linear Embeddings (LLE) – Roweis

75. Escalonamento Multidimensional
• Multidimensional Scaling (MDS)
• Objetivo diferente:
▫ Encontrar um conjunto de pontos cujas distâncias
entre pares correspondem a uma dada matriz de
distância.

76. MDS Clássico x PCA
• MDS
▫ Dada uma matriz n x n de distância de pares entre
pontos.
 Calcular a matrix X n x k de coordenadas de pontos a
partir de D com uso de álgebra linear.
 Resumindo: transformar distâncias em coordenadas.
 Não trivial, mas possível através de métodos lineares.
▫ MSD clássico tem desempenho melhor que PCA
nessa matrix X.
▫ Essencialmente os mesmos resultados, mas a
partir de diferentes entradas.

77. Imagens coloridas

78. Amigos no Facebook

79. IN-SPIRE, PNNL
Classificação de
documentos.
MSD em
documentos.

80. Regis Pires Magalhães
regismagalhaes@ufc.br
Obrigado!
Dúvidas, comentários, sugestões?