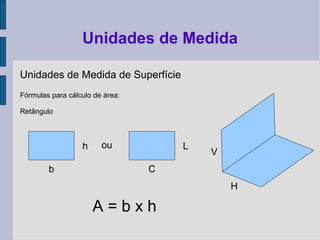
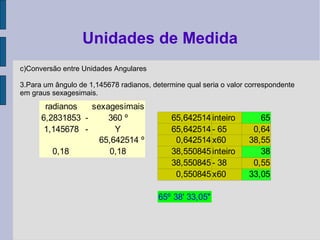
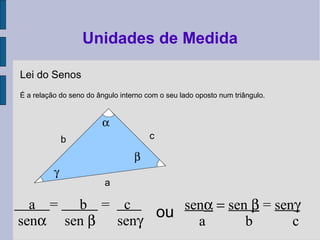
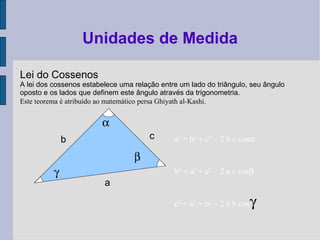
O documento descreve as principais unidades de medida utilizadas em topografia, incluindo unidades lineares, angulares, de área, volume e conversões entre elas. São listadas unidades como metro, quilômetro, grau, radiano e fórmulas para cálculo de áreas de figuras planas.

1. Unidades de
Medida

2. Em Topografia, são medidas duas espécies de grandezas:
as lineares para comprimento, largura e altura e
as angulares para indicação de direção,
mas, na verdade, outras duas espécies de grandezas são também trabalhadas:
as de superfície para áreas e
as de volume para terraplenagem, concretagem, etc.
O sistema de unidades utilizado no Brasil é o Métrico Decimal, porém, em
função dos equipamentos e da bibliografia utilizada, na sua grande maioria
importada, algumas unidades relacionadas abaixo apresentarão seus valores
correspondentes no sistema Americano, ou seja, em Pés/Polegadas.
A seguir encontram-se as unidades mais comumente utilizadas para expressar
cada uma das grandezas mencionadas.
Unidades de Medida

3. Unidades de Medida Linear
µm(E-06 ou 10-6
), mm(E-03 ou 10-3
), cm(E-02 ou 10-2
), dm(E-01 ou 10-1
), m e
Km(E+03 ou 10+3
)
polegada = 2,75 cm = 0,0275 m
polegada inglesa = 2,54 cm = 0,0254 m
pé = 30,48cm = 0,3048 m
jarda = 91,44cm = 0,9144m
milha brasileira = 2200 m
milha terrestre/inglesa = 1609,31 m
Unidades de Medida

4. Unidades de Medida Angular
Para as medidas angulares têm-se a seguintes unidades:
Graus Sexagesimal
0 - 360º (359) e 0 – 59' e 0 – 59,99”
243º 27' 34,79”
onde se lê
243 graus, 27 minutos e 34,79 segundos
Unidades de Medida

5. Unidades de Medida Angular
Para as medidas angulares têm-se a seguintes unidades:
Graus Decimal
0 - 359,999999º
243º 27' 34,79” = 243,45966388888888888888888888889º ou 243,459664º
onde se lê
243,459664 graus decimal
Unidades de Medida

6. Unidades de Medida Angular
Para as medidas angulares têm-se a seguintes unidades:
Grados
0 - 400g
243º 27' 34,79” = 243,459664º = 270,510738g
onde se lê
270,510738 grados
Unidades de Medida

7. Unidades de Medida Angular
Para as medidas angulares têm-se a seguintes unidades:
Radianos
0 - 2¶
243º 27' 34,79” = 243,459664º = 270,510738g = 4,249173 Rad
onde se lê
4,249173 Radianos
Unidades de Medida

8. Unidades de Medida Angular
Para as medidas angulares têm-se a seguinte relação:
360º = 400g = 2¶
onde
º – GRAUS
g – GRADUS
RADIANOS onde ¶ = 3,141592.
Atenção:
As unidades angulares devem ser trabalhadas sempre
com seis (6) casas decimais.
As demais unidades, com duas (2) casas decimais.
Unidades de Medida

9. Unidades de Medida de Superfície
Áreas
cm²(E-04), m² e Km²(E+06)
are = 100 m²
acre = 4.046,86 m²
hectare (ha) = 10.000 m²
alqueire paulista (menor) = 2,42 ha = 24.200 m²
alqueire mineiro (geométrico) = 4,84 ha = 48.400 m2
Unidades de Medida

10. Unidades de Medida de Superfície
Fórmulas para cálculo de área:
Retângulo
Unidades de Medida
b
h
C
Lou
A = b x h
H
V

11. Unidades de Medida de Superfície
Fórmulas para cálculo de área:
Triângulo
Unidades de Medida
b
h
ou
b x h
2
A =
b
h
h
2
A = b x

12. Unidades de Medida de Superfície
Fórmulas para cálculo de área:
Trapézio
Unidades de Medida
b
h2
ou
h1
x h1
2
A = b x h
2
A = b x
h1
b
hm

13. Unidades de Medida de Superfície
Fórmulas para cálculo de área:
Circunferência
Unidades de Medida
A = ¶ x r²r

14. Unidades de Medida de Volume
m³
1 litro = 10cm x 10cm x 10cm = 1dm x 1dm x 1dm = 1dm³
ou
1 litro = 0,001 m³
Unidades de Medida

15. Arredondamento
Se o digito a ser arredondado estiver entre 0 e 4, desprezar os dígitos restantes.
Se o digito a ser arredondado estiver entre 5 e 9, somar 1 na casa do dígito logo a
esquerda.
Exemplos:
3,152946
arredondando para 5 casas decimais o 6º digito é 6, portanto o valor fica 3,15295
arredondando para 4 casas decimais o 5º digito é 4, portanto o valor fica 3,1529
arredondando para 3 casas decimais o 4º digito é 9, portanto o valor fica 3,153
arredondando para 2 casas decimais o 3º digito é 2, portanto o valor fica 3,15
arredondando para 1 casas decimais o 2º digito é 5, portanto o valor fica 3,2
arredondando para 0 casas decimais o 1º digito é 1, portanto o valor fica 3
Unidades de Medida

16. a)Conversão entre Unidades Lineares
1)Tem-se para a medida da distância horizontal entre dois pontos o valor de
1.290,9078 polegadas inglesa. Qual seria o valor desta mesma medida em
quilômetros?
2)O lado de um terreno mede 26,50 metros. Qual seria o valor deste mesmo lado em
polegadas inglesas?
3)Determine o valor em milhas inglesas, para uma distância horizontal entre dois
pontos de 74,9 milhas brasileiras.
Unidades de Medida
Exercícios

17. a)Conversão entre Unidades Lineares
1.Tem-se para a medida da distância horizontal entre dois pontos o valor de
1.290,9078 polegadas inglesa. Qual seria o valor desta mesma medida em
quilômetros?
Sendo:
1 polegada inglesa = 2,54 cm = 0,0254 m
1.290,9078 polegadas inglesa = X
1X = 0,0254 x 1290,9078
X = 32,7890581 m
Sendo:
1 m = 0,001 km
32,7890581 m = Y
Y = 32,7890581 x 0,001 = 0,0327890581
arredondando na 2 casa 0,03 km
Unidades de Medida
Exercícios

18. a)Conversão entre Unidades Lineares
2.O lado de um terreno mede 26,50 metros. Qual seria o valor deste mesmo lado em
polegadas inglesas?
Sendo:
1 polegada inglesa = 0,0254 m
X polegadas inglesa = 26,50 m
0,0254X = 1 x 26,50
X = 26,50 = 1043,30709 polegadas inglesas
0,0254
Unidades de Medida
Exercícios

19. a)Conversão entre Unidades Lineares
3.Determine o valor em milhas inglesas, para uma distância horizontal entre dois
pontos de 74,9 milhas brasileiras.
Sendo:
1 milha brasileira = 2200 m
74,9 milhas brasileiras = X m
1X = 2200 x 74,9 = 164780 m
1 milha inglesa = 1609,31 m
Y milha inglesa = 164780 m
Y = 164780 = 102,391708 ou 102,39 milhas inglesas
1609,31
Unidades de Medida
Exercícios

20. b)Conversão entre Unidades de Superfície
1.Determine o valor em alqueires menor, para um terreno de área igual a 1224,567 m².
2.Determine o valor em hectares, para um terreno de área igual a 58.675,5678 m².
3.Determine o valor em acres, para um terreno de área igual a 18,15 alqueires paulista.
Unidades de Medida

21. b)Conversão entre Unidades de Superfície
1.Determine o valor em alqueires menor, para um terreno de área igual a 1224,567 m².
Unidades de Medida
alqueires p. m²
1 - 24200
Y - 1224,567
1x1224,567=Yx24200
0,05

22. b)Conversão entre Unidades de Superfície
2.Determine o valor em hectares, para um terreno de área igual a 58.675,5678 metros
quadrados.
Unidades de Medida
ha m²
1 10000
Y - 58675,568
1x58675,5678=Yx10000
5,87

23. b)Conversão entre Unidades de Superfície
3.Determine o valor em acres, para um terreno de área igual a 18,15 alqueires paulista.
Unidades de Medida
acre m²
1 4046,86
X - 439230,00
1x439230=Xx4046,86
108,54
alqueires p. m²
1 - 24200
18,15 - Y
1xY=18,15x24200
439230,00

24. c)Conversão entre Unidades Angulares
1)Determine o valor em graus centesimais (centésimos e milésimos de grau) para o
ângulo sexagesimais 275º 24' 48,95".
2)Determine o valor em grados centesimais (centésimos e milésimos de grado) e em
radianos para o ângulo de 157º 17' 30,65".
3)Para um ângulo de 1,145678 radianos, determine qual seria o valor correspondente
em graus sexagesimais.
4)Para um ângulo de 203,456789 grados decimais, determine qual seria o valor
correspondente em graus decimais.
Unidades de Medida

25. c)Conversão entre Unidades Angulares
1)Determine o valor em graus centesimais (centésimos e milésimos de grau) para o
ângulo sexagesimais 275º 24' 48,95".
Unidades de Medida

26. c)Conversão entre Unidades Angulares
2.Determine o valor em grados centesimais (centésimos e milésimos de grado) e em
radianos para o ângulo de 157º 17' 30,65".
Unidades de Medida
sexagesimais gradus radianos
360 º - 400 - 6,2831853
157º17' 30,65” - Y - Z
157 + 17/60 + 30,65/3600
157,291847 º 174,768719 2,745
0,44 0,44 0,44

27. c)Conversão entre Unidades Angulares
3.Para um ângulo de 1,145678 radianos, determine qual seria o valor correspondente
em graus sexagesimais.
Unidades de Medida
radianos sexagesimais
6,2831853 - 360 º 65,642514inteiro 65
1,145678 - Y 65,642514- 65 0,64
65,642514 º 0,642514x60 38,55
0,18 0,18 38,550845inteiro 38
38,550845- 38 0,55
0,550845x60 33,05
65º 38' 33,05''

28. c)Conversão entre Unidades Angulares
4.Para um ângulo de 203,456789 grados decimais, determine qual seria o valor
correspondente em graus decimais.
Unidades de Medida
gradus sexagesimais
400 - 360 º
203,457 - Y
183,111110 º
0,51 0,51

29. d)Conversão entre Unidades de Volume
1.Determine o valor em litros, para um volume de 12,34 m³.
2.Determine o valor em m³, para um volume de 15.362,56 litros.
Unidades de Medida

30. d)Conversão entre Unidades de Volume
1.Determine o valor em litros, para um volume de 12,34 m³.
Unidades de Medida
m³ litros
1 - 1000
12,34 - Y
1xY=12,34x1000
12340

31. d)Conversão entre Unidades de Volume
2.Determine o valor em m³, para um volume de 15.362,56 litros.
Unidades de Medida
m³ litros
1 - 1000
Y - 15362,56
1x15362,56=Yx1000
15,36

32. Exercícios Propostos
1.Dado o ângulo de 1,573498 radianos, determine o valor correspondente em grados
decimais.
2.Sabendo-se que um alqueire geométrico eqüivale a um terreno de 220mx220m;
que um acre eqüivale a 4046,86m²; e que uma porção da superfície do terreno
medida possui 3,8 alqueires geométrico de área, determine a área desta mesma
porção, em acres.
3.Dado o ângulo de 120º 35' 48”, determine o valor correspondente em grados
centesimais.
Unidades de Medida

33. Exercícios Propostos
1.Dado o ângulo de 1,573498 radianos, determine o valor correspondente em grados
decimais.
Unidades de Medida
gradus radianos
400 - 6,2831853
Y - 1,5734980
100,171994
0,250430 0,250

34. Exercícios Propostos
2.Sabendo-se que um alqueire geométrico eqüivale a um terreno de 220mx220m;
que um acre eqüivale a 4046,86m²; e que uma porção da superfície do terreno
medida possui 3,8 alqueires geométrico de área, determine a área desta mesma
porção, em acres.
Unidades de Medida
alqueires m²
1 - 48400
3,8 - Y
1xY=3,8x48400
183920,00
acre m²
1 - 4046,86
Y - 183920,00
1x183920=Yx4046,86
45,45

35. Exercícios Propostos
3.Dado o ângulo de 120º 35' 48”, determine o valor correspondente em grados
centesimais.
Unidades de Medida
sexagesimais gradus
360 º - 400
120º 35' 48” - Y
157 + 17/60 + 30,65/3600
157,291847 º 174,768719
0,44 0,44

36. Lei do Senos

37. Lei do Senos
É a relação do seno do ângulo interno com o seu lado oposto num triângulo.
Unidades de Medida
b c
a
ou senα = sen β = senγ
a b c
a = b = c
senα sen β senγ
α
β
γ

38. Lei do Cosseno

39. Lei do Cossenos
A lei dos cossenos estabelece uma relação entre um lado do triângulo, seu ângulo
oposto e os lados que definem este ângulo através da trigonometria.
Este teorema é atribuído ao matemático persa Ghiyath al-Kashi.
Unidades de Medida
b c
a
a² = b² + c² – 2 b c cosα
b² = a² + c² – 2 a c cosβ
c² = a² + b² – 2 a b cosγ
α
β
γ

40. Atenção:
As somatória dos ângulos internos de um triângulo é
igual a 180º.
Unidades de Medida