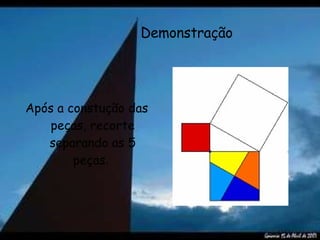
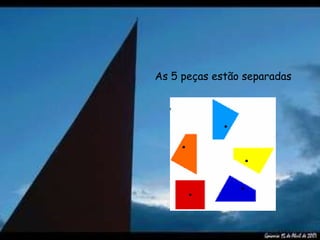
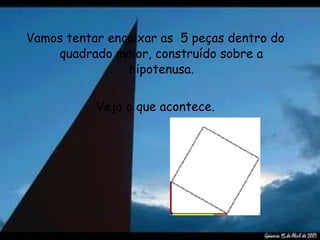
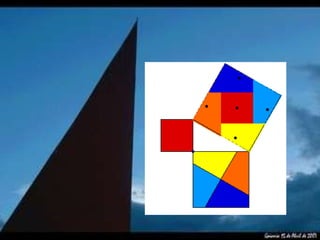
O documento descreve o Teorema de Pitágoras e como demonstrá-lo usando um quebra-cabeça. Ele afirma que o Teorema diz que o quadrado da hipotenusa de um triângulo retângulo é igual à soma dos quadrados dos catetos. Em seguida, apresenta uma demonstração usando peças recortadas de um quebra-cabeça para verificar se a área do quadrado maior é igual à soma das áreas dos dois quadrados menores.

1. Teorema de Pitágoras Quebra-cabeça

2. Teorema Como sabemos, o Teorema de Pitágoras diz que, em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Se construírmos quadrados sobre os lados a, b e c do triângulo retângulo, esses quadrados terão área a2, b 2 e c2 .

3. Ou seja, podemos enunciar o Teorema de Pitágoras da seguinte forma: A área do quadrado maior (construído sobre a hipotenusa) é igual à soma das áreas dos dois quadrados menores (construídos sobre os catetos).

4. Demonstração Vamos, então, trabalhar com demonstrações do Teorema de Pitágoras através de recortes. Com o auxílio do quebra-cabeça, vamos verificar se a área do quadrado maior é igual a soma da área dos dois quadrados menores.

5. Demonstração Após a constução das peças, recorte separando as 5 peças.

6. As 5 peças estão separadas

7. Vamos tentar encaixar as 5 peças dentro do quadrado maior, construído sobre a hipotenusa. Veja o que acontece.