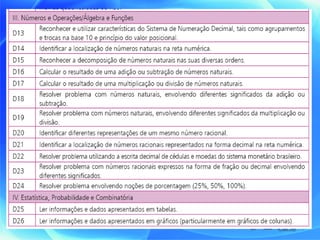
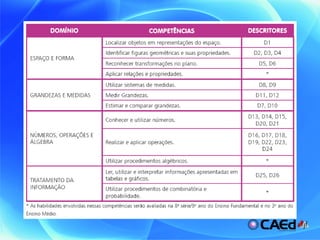
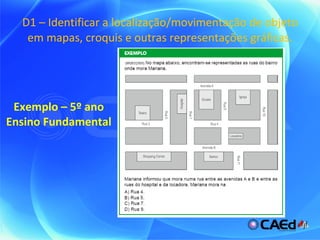
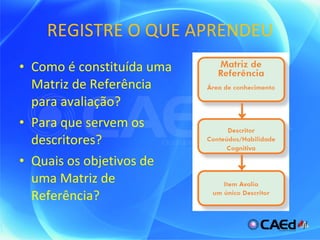
O documento apresenta uma matriz de referência para avaliação em matemática do 4o ao 5o ano, com os seguintes tópicos: espaço e forma, grandezas e medidas, números, operações e álgebra, e tratamento da informação. Cada tópico contém descritores que indicam habilidades a serem avaliadas, como identificar localização em mapas, resolver problemas envolvendo perímetro e porcentagens.