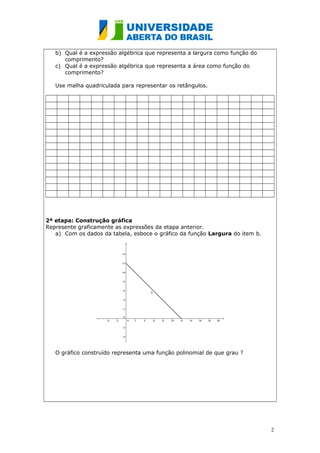
Este projeto ensina sobre funções quadráticas através de um observatório de parábolas. Os alunos irão completar tabelas, construir gráficos e resolver problemas envolvendo comprimento, largura e área de retângulos para entender melhor as expressões algébricas e representações gráficas de funções do segundo grau.

1. Informática Educativa I :: Projeto em Informática Educativa
Título: Observatório das Parábolas
Nome do Aluno: Juciara Gonçalves de Oliveira
1. Disciplina e anos envolvidos:
Matemática
1º ano do ensino médio é o público alvo para a realização do projeto.
2. Tema central :
Estudando a função quadrática e sua representação
3. Temas de apoio:
Equação algébrica
Gráfico
4. Justificativa:
No mundo atual somos estimulados a relacionar grandezas e a identificar formas
equivalentes em vários contextos.
O estudo da função quadrática contribui para o conhecimento de fatos do cotidiano
e oferece a possibilidade dar significado aos conteúdos matemáticos que serão
retomados nas série seguintes oferecendo assim ao estudante um entendimento
mais significativo sobre a Matemática.
5. Objetivos gerais e específicos:
Objetivo geral
Utilizar a função do 2o grau para resolver problemas.
Objetivo específico
Associar uma situação problema envolvendo grandezas e função com a expressão
algébrica e o gráfico que a representa.
6. Enfoque pedagógico :
Trabalhar promovendo o desenvolvimento da ciência cognitiva associada a
ambientes informatizados promovendo novos modelos e referencias para ampliar
investigações sobre os processos cognitivos.
7. Recursos tecnológicos:
Malha quadriculada
Software Geogebra
Atividade impressa
8. Etapas e suas estratégias de realização:
Três etapas
1ª etapa: Situação problema
Rafael deseja comparar os gráficos de um retângulo que tem um perímetro fixo de
24 centímetros. Ao aumentar o comprimento com 1 centímetro, tanto a medida da
largura como da área vão variar.Vamos auxiliar Rafael respondendo os itens a
seguir:
a) Complete a tabela idealizada por Rafael:
C 1 2 3 4 6 7 8 9 10 11
L 11 9 8 7 6 5 4 3 2 1
A 11 20 27 32 35 36 35 32 20 11
Onde: C= comprimento, L= largura , A= área
1

2. b) Qual é a expressão algébrica que representa a largura como função do
comprimento?
c) Qual é a expressão algébrica que representa a área como função do
comprimento?
Use malha quadriculada para representar os retângulos.
2ª etapa: Construção gráfica
Represente graficamente as expressões da etapa anterior.
a) Com os dados da tabela, esboce o gráfico da função Largura do item b.
O gráfico construído representa uma função polinomial de que grau ?
2

3. b) Com os dados da tabela, esboce o gráfico da função área do item c.
b) O gráfico construído representa uma função polinomial de que grau ?
c) Analisando o gráfico acima, qual foi a área máxima obtida no retângulo?
Quais as suas dimensões?
d) Se a largura do retângulo fosse 3,5 cm, qual seria o comprimento e a sua
área?
3

4. 3ª etapa: Representação algébrica
1- (ENEM-2002,adaptada) Um forro retangular de tecido traz em sua etiqueta a
informação de que encolherá após a primeira lavagem, mantendo, entretanto,
seu formato.A figura a seguir mostra as medidas originais do forro e o tamanho
do encolhimento no comprimento e na largura, representado por x.
Nessas condições, a área perdida (A) do forro após a primeira lavagem será
expressa pela função :
a) A(x) = x²
b) A(x) = -2x + 16
c) A(x) = -x² + 15
d) A(x) = -x² + 8x
e) A(x) = x² - 8x + 15
2- A medida da área de um retângulo é calculada através do produto entre as
medidas de seu comprimento e sua largura.Observe a representação abaixo de
um projeto feito por um arquiteto para transformar um quarto retangular e um
escritório quadrado em uma única sala com 33m² de área.
a) 8x² = 33
b) x² + 8=33
c) x² + 8x=33
d) x² - 8x = 33
e) 2x² 16x = 33
4

5. 3- Em um condomínio, todos os lotes sã retangulares, cujo lados são iguais ou
superiores a 15 m. A medida da áreas de cada um desses lotes é dada pela
função M(x)= 80x- x², em que M(x) representa a área, em metros quadrados, e
x representa a medida do comprimento do retângulo, em metros. João comprou
lotes de 700m² nesse condomínio. Qual é a medida, em metros, do
comprimento d lote que João comprou?
a) 20
b) 25
c) 55
d) 70
e) 80
4- A diferença entre o triplo do quadrad de um número natural e 90 é igual a
153.Qual é esse número?
5-Um fazendeiro tem 100 metros de arame para delimitar um curral de forma
retangular. Quais as dimensões do curral para que a área cercada seja máxima?
a) 20 m
b) 25 m
c) 55 m
d) 70 m
e) 80 m
As tarefas devem ser realizadas em grupo preservando a formação inicial se
possível com registros individuais e de forma colaborativa .
09. Definições de Papéis :
Aluno como protagonista do seu próprio conhecimento;
Professor como facilitador, mediador e colaborativo para que o grupo tenha um
bom rendimento das atividades propostas.
10.Sites e bibliografia de apoio:
-http://www.uff.br/cdme/fqa/fqa-html/fqa-gs-mathml-br.html
-Contexto&Aplicações, vol.1. Luiz Roberto Dante
-Apostila do Programa Reforço Escolar -Parábolas em Ação da Seeduc rj
11. Coleta de dados:
Internet, livros, jornais e outros
12. Seleção do material:
Malha quadriculada e cartolina colorida
Atividade do reforço escolar
Sala de informática
13. Programação visual:
Power pointer
14. Meios para a execução:
Sala de aula e laboratório de informática
5

6. 15. Avaliação:
O aluno deverá registrar e relatar se houve ou não mudança de seu entendimento
quanto a representação gráfica e algébrica de uma função.
16. Cronograma:
As atividades devem levar 6 aulas com duração de 50minutos cada.
6

7. 15. Avaliação:
O aluno deverá registrar e relatar se houve ou não mudança de seu entendimento
quanto a representação gráfica e algébrica de uma função.
16. Cronograma:
As atividades devem levar 6 aulas com duração de 50minutos cada.
6