Baixado 37 vezes
Carregado porBaguiasri
PI
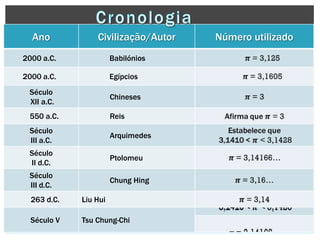
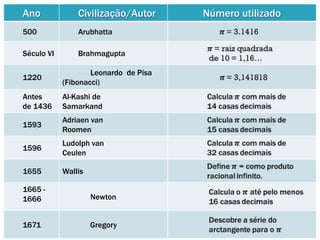
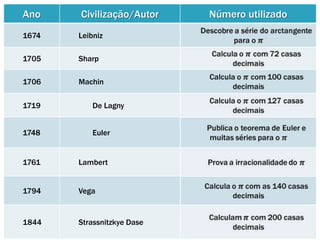
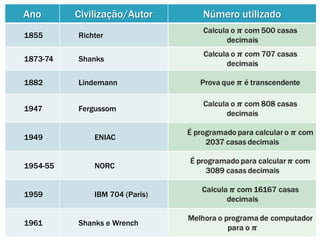
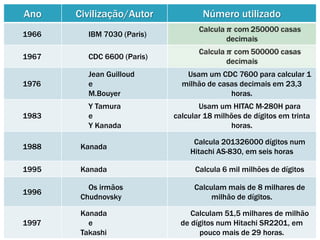
Pi é um número irracional que representa a razão entre a circunferência e o diâmetro de um círculo. Suas primeiras estimativas foram feitas por civilizações antigas como os babilônios e egípcios, mas Arquimedes foi o primeiro a calcular aproximações precisas de pi usando polígonos inscritos e circunscritos em círculos. Ao longo dos séculos, matemáticos de diversas culturas melhoraram as aproximações de pi, e atualmente bilhões de dígitos foram calculados us
Mais conteúdo relacionado
PI
- 1. História do Pi Como se sabe, pi é o número mais famoso da história universal, o qual recebeu esse nome, um nome grego, porque embora seja um número, não pode ser escrito como um número decimal com um número finito de algarismos. Representa a razão entre o perímetro de qualquer circunferência e o seu diâmetro. Os primeiros vestígios de uma estimativa de pi, encontram-se no Papiro de Rhind escrito, aproximadamente, em 1700 a.C. , onde se lê: "a área de um círculo é igual à de um quadrado cujo lado é o diâmetro do círculo diminuído da sua nona parte".
- 2. No velhotestamento (I Reis 7: 23) lê-se: "E ele (Salomão) fez também um lago de dez cúbitos, de margem a margem, circular, cinco cúbitos de fundo, e trinta cúbitos em redor", este mesmo verso aparece também em II Crónicas 4:2. Hebreus Os antigos Hebreus contentavam-se em atribuir a pi o valor 3. Este valor foi possivelmente encontrado por medição.
- 3. O valor3 foi usado durante muito tempo por motivos religiosos e culturais em certas civilizações, como a dos Egípcios e a dos Babilónios, quando já se conheciam nessas mesmas civilizações determinações melhores. A melhor aproximação do pi encontra-se na bíblia, como já referimos... "Fez o tanque de fundição, redondo, com 10 côvados de diâmetro, 5 côvados de altura e 30 de circunferência".
- 4. Arquimedes deSiracusa (287-212 a.C.) pôs mãos à obra com novas experiências, muito profundas. Suspeitava que o pi não era racionalmente determinável. Assim sendo, propôs-se descobrir um processo para a determinação de pi, o Método de Arquimedes, com a precisão que se desejasse. Este usou, processos geométricos, complicados mas gerais, que dão limites inferiores e superiores para pi. Arquimedes utilizou alguns polígonos regulares que inscrevia e circunscrevia a uma circunferência, com um número crescente de lados, até chegar ao polígono de 96 lados, através do qual obteve a seguinte aproximação de pi:
- 5. No entanto Hui(263 d. C.) descobriu, também, através de polígonos regulares inscritos e circunscritos que: Dois séculos mais tarde, no ano 480 da nossa era, um certo engenheiro hidráulico chinês de nome Tsu ChungChi (430-501 d.C.), chegou a um valor de pi extraordinariamente preciso, considerada a época em que foi calculado. O pi de Tsu Chung-Chi, na nossa notação decimal, oscilaria entre 3,1415926 e 3,1415927. Desconhece-se como é que ele chegou a este resultado.
- 6. Na Índia (Séc.V e VI) Aryabhata, (476-550), na sua obra "Aryabhatiya", enuncie: "Junte 4 a 100, multiplique por 8, junte ainda 62.000, ter-se-á assim para um diâmetro de duas míriadas (20.000), o comprimento aproximado da circunferência".
- 7. Frederico II, decognome "stupor mundi" (o espanto do mundo), partiu do valor de Arquimedes 22/7, a que chamou inexacto e, conhecendo o valor 377/120 calculado por Ptolomeu, calculou um valor a que chamou "exacto".
- 8. Um Inglês chamadoShanks, usou a fórmula de Machin para calcular o pi até às 707 casas decimais, das quais só 527 estavam corretas, publicando o resultado do seu trabalho em 1873. Em 1961, conseguiu-se através da computação a aproximação do pi com 100 265 casas decimais. Mais tarde em 1967 aproximou-se até às 500 000 casas decimais. Em 1949 usou-se um computador para calcular o pi até às 2000 casas decimais.
- 9. Recentemente, David Bailey,Peter Borwein e Simon Plouffe contabilizaram 10 bilhões de casas decimais para pi, usando uma fórmula que dá cada casa decimal do pi individualmente, para cada k escolhido.
- 10. É ainda importantefocar, que o primeiro a utilizar o símbolo pi, com o significado que este tem hoje em dia, foi o matemático inglês William Jones em 1706. O matemático suíço Leonhard Euler em 1737 adotou o símbolo que rapidamente se tornou uma notação standard.
- 11. Onde se utilizao PI: PI de circunferências: É a constante de proporcionalidade direta entre os comprimentos de círculos e os respetivos diâmetros na razão entre a circunferência de um círculo e seu diâmetro
- 12. PI deáreas de círculos: É a constante de proporcionalidade direta na razão entre a área de um círculo e o quadrado do seu diâmetro
- 13.
- 14. Ano Civilização/Autor 2000 a.C. Babilónios 2000 a.C. Egípcios Século XIIa.C. Chineses 550 a.C. Reis Século III a.C. Arquimedes Século II d.C. Ptolomeu Século III d.C. Chung Hing 263 d.C. Liu Hui Século V Tsu Chung-Chi Número utilizado
- 15. Ano Civilização/Autor 500 Arubhatta Século VI Brahmagupta 1220 Leonardo dePisa (Fibonacci) Antes de 1436 Al-Kashi de Samarkand 1593 Adriaen van Roomen 1596 Ludolph van Ceulen 1655 Wallis 1665 1666 Newton 1671 Gregory Número utilizado
- 16.
- 17.
- 18. Ano Civilização/Autor 1966 IBM 7030 (Paris) 1967 CDC6600 (Paris) 1976 Jean Guilloud e M.Bouyer 1983 Y Tamura e Y Kanada Número utilizado Usam um CDC 7600 para calcular 1 milhão de casas decimais em 23,3 horas. Usam um HITAC M-280H para calcular 18 milhões de dígitos em trinta horas. 1988 Kanada Calcula 201326000 dígitos num Hitachi AS-830, em seis horas 1995 Kanada Calcula 6 mil milhões de dígitos 1996 Os irmãos Chudnovsky Calculam mais de 8 milhares de milhão de dígitos. 1997 Kanada e Takashi Calculam 51,5 milhares de milhão de dígitos num Hitachi SR2201, em pouco mais de 29 horas.
- 19. MNEMÓNICA Esta mnemónicarealizada pelo grupo, com a ajuda da nossa professora, serve para memorizar alguns dos algarismos do pi (π) : 3 ,1 2 5 4 1 5 6 9 5 8 3 9