1) O documento discute a história da matemática chinesa, desde os primeiros registros no período Shang até contribuições de matemáticos como Chu Shï-kié no século XIII.
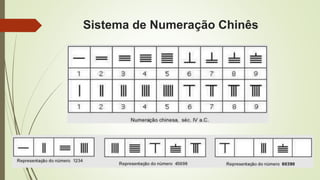
2) A China desenvolveu um sofisticado sistema de numeração posicional decimal e reconheceu os números negativos muito antes do Ocidente.
3) Matemáticos chineses como Liu Hui e Ch'in Kiu-shao realizaram cálculos precisos de pi e desenvolveram métodos algébricos como o de