Baixado 26 vezes
Carregado porBaguiasri
PI - 3,14....
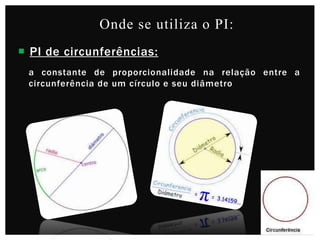
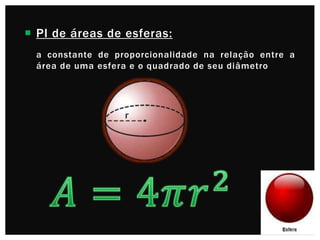
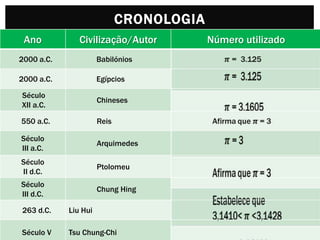
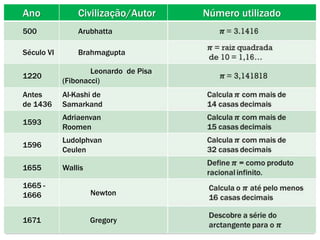
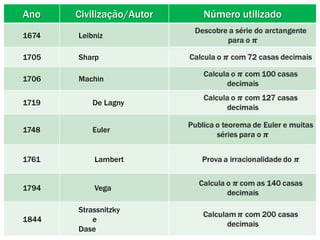
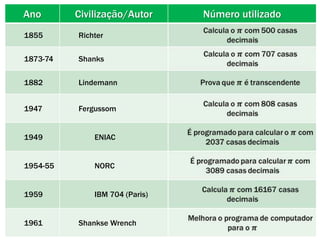
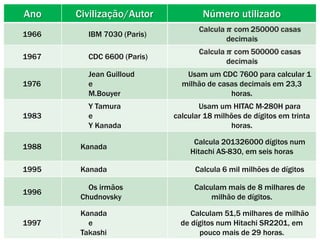
O documento descreve a história do número pi. Começa com estimativas antigas de pi por babilônios e egípcios. Arquimedes foi o primeiro a calcular pi com precisão usando polígonos inscritos em círculos. Ao longo dos séculos, matemáticos de diversas civilizações melhoraram as aproximações de pi, culminando nos cálculos de milhões de dígitos décimais por computadores modernos.
Mais conteúdo relacionado
PI - 3,14....
- 1.
- 2. História do Pi Como se sabe pi é o número mais famoso da história universal, no qual recebeu um nome próprio, um nome grego, pois embora seja um número, não pode ser escrito como um número finito de algarismos. Os primeiros vestígios de uma estimativa de pi, encontram-se no Papiro de Rhind escrito, aproximadamente, em 1700 a.C. , onde se lê: "a área de um círculo é igual a de um quadrado cujo lado é o diâmetro de círculo diminuído de sua nona parte".
- 3. No velhotestamento (I Reis 7: 23) lê-se: "E ele (Salomão) fez também um lago de dez cúbitos, de margem a margem, circular, cinco cúbitos de fundo, e trinta cúbitos em redor", este mesmo verso aparece também em II Crónicas 4:2. Hebreus Os antigos Hebreus se contentavam em atribuir a pi o valor 3. Este valor foi possívelmente encontrado por medição.
- 4. O valor3 foi usado durante muito tempo por motivos religiosos e culturais em certas civilizações, como a dos Egípcios e a dos Babilónios, quando já se conheciam nessas mesmas civilizações determinações melhores. Nas matemáticas babilónicas a melhor aproximação do pi é a bíblia, como já referimos... "Fez o tanque de fundição, redondo, com 10 côvados de diâmetro, 5 côvados de altura e 30 de circunferência".
- 5. Arquimedes deSiracusa (287-212 a.C.) pôs mãos à obra com novas experiências, muito profundos. Suspeitava que o pi não era racionalmente determinável. Assim sendo, propôs-se descobrir um processo para a determinação de pi, o Método de Arquimedes, com a precisão que se desejasse. Este usou, processos geométricos, complicados mas gerais, que dão limites inferiores e superiores para pi. Arquimedes utilizou alguns polígonos regulares, com um número crescente de lados, até chegar ao polígono de 96 lados, através do qual obteve a seguinte aproximação de pi:
- 6. No entanto Hui(263 d. C.) descobriu, através de polígonos regulares inscritos e circunscritos que: Dois séculos mais tarde, no ano 480 da nossa era, um certo engenheiro hidráulico chinês de nome Tsu ChungChi (430-501 d.C.), chegou a um valor de pi extraordinariamente preciso, considerada a época em que foi calculado. O pi de Tsu Chung-Chi, em nossa notação decimal, oscilaria entre 3,1415926 e 3,1415927. Sendo desconhecido como é que ele chegou a este resultado.
- 7. Na Índia (Séc.V e VI) Aryabhata, (476-550), na sua obra "Aryabhatiya", enuncie: "Junte 4 a 100, multiplique por 8, junte ainda 62.000, ter-se-á assim para um diâmetro de duas míriadas (20.000), o comprimento aproximado da circunferência". Na Itália (Séc. XIII), o Papa Inocêncio III, governava os estados pontifícios desde 1198 e, em 1212 conseguiu proclamar o seu pupilo Frederico II, rei da Germânia e, na corte deste monarca, em Itália, se notabilizou Leonardo Fibonnaci.
- 8. Frederico II, decognome "stupor mundi" (o espanto do mundo), partiu do valor de Arquimedes 22/7, a que chamou inexacto e, conhecendo o valor 377/120 calculado por Ptolomeu, calculou um valor a que chamou "exacto". Na época do Renascimento houve na devida altura, um novo mundo matemático. Entretanto, descobriu-se que a definição não geométrica de pi e do papel "não geométrico" deste valor. Assim chegou à descoberta das representações de pi por séries infinitas.
- 9. Um Inglês chamadoShanks, usou a fórmula de Machin para calcular pi até às 707 casas decimais, das quais só 527 estavam correctas, publicando o resultado do seu trabalho em 1873. Em 1949 um computador foi usado para calcular o pi até às 2000 casas decimais. Em 1961 conseguiu-se através de computação a aproximação de pi através de 100 265 casas decimais, mais tarde em 1967 aproximou-se até às 500 000 casas decimais.
- 10. Recentemente, David Bailey,Peter Borwein e Simon Plouffe contabilizaram 10 bilhões de casas decimais para pi, usando uma fórmula que dá cada casa decimal do pi individualmente, para cada k escolhido.
- 11. O matemático suíçoLeonhard Euler em 1737 adoptou o símbolo que rapidamente se tornou uma notação standard.
- 12. Onde se utilizao PI: PI de circunferências: a constante de proporcionalidade na relação entre a circunferência de um círculo e seu diâmetro
- 13. PI deáreas de círculos: a constante de proporcionalidade na relação entre a área de um círculo e o quadrado de seu diâmetro
- 14. PI deáreas de esferas: a constante de proporcionalidade na relação entre a área de uma esfera e o quadrado de seu diâmetro
- 15. PI devolumes de esferas: a constante de proporcionalidade na relação entre o volume de uma esfera e o cubo de seu diâmetro
- 16.
- 17. CRONOLOGIA Ano Civilização/Autor 2000 a.C. Babilónios 2000 a.C. Egípcios Século XIIa.C. Chineses 550 a.C. Reis Século III a.C. Arquimedes Século II d.C. Ptolomeu Século III d.C. Chung Hing 263 d.C. Liu Hui Século V Tsu Chung-Chi Número utilizado
- 18. Ano Civilização/Autor 500 Arubhatta Século VI Brahmagupta 1220 Leonardo dePisa (Fibonacci) Antes de 1436 Al-Kashi de Samarkand 1593 Adriaenvan Roomen 1596 Ludolphvan Ceulen 1655 Wallis 1665 1666 Newton 1671 Gregory Número utilizado
- 19.
- 20.
- 21. Ano Civilização/Autor 1966 IBM 7030 (Paris) 1967 CDC6600 (Paris) 1976 Jean Guilloud e M.Bouyer 1983 Y Tamura e Y Kanada Número utilizado Usam um CDC 7600 para calcular 1 milhão de casas decimais em 23,3 horas. Usam um HITAC M-280H para calcular 18 milhões de dígitos em trinta horas. 1988 Kanada Calcula 201326000 dígitos num Hitachi AS-830, em seis horas 1995 Kanada Calcula 6 mil milhões de dígitos 1996 Os irmãos Chudnovsky Calculam mais de 8 milhares de milhão de dígitos. 1997 Kanada e Takashi Calculam 51,5 milhares de milhão de dígitos num Hitachi SR2201, em pouco mais de 29 horas.
- 22. MNEMÓNICA Esta mnemónicarealizada pelo grupo serve para ajudar a fixar alguns dos números do pi (π) : 3 , 1 2 5 4 1 6 5 9 5 8 3 9
- 23. WEB GRAFIA http://www.slideshare.net/sextoc2012/a-histria-do-pi http://www.educ.fc.ul.pt/icm/icm98/icm11/historiadopibot ao.htm http://www.educ.fc.ul.pt/icm/icm2001/icm34/indice.htm http://www.fmboschetto.it/didattica/Pi_mnemonics/Pi %20 Mnemonics.htm http://www.mundovestibular.com.br/articles/204/1/ONUMERO-PI/Paacutegina1.html http://www.educ.fc.ul.pt/icm/icm2001/icm34/historia.htm http://www.coladaweb.com/matematica/numero-pi http://www.mat.ufrgs.br/~portosil/aplcom1a.html