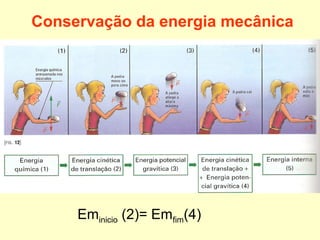
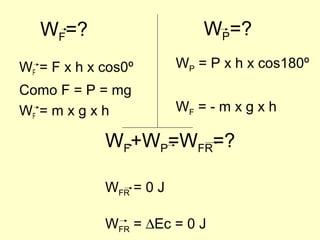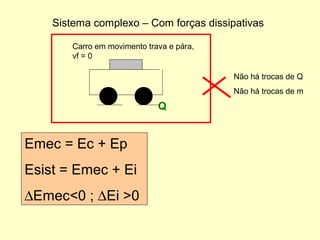
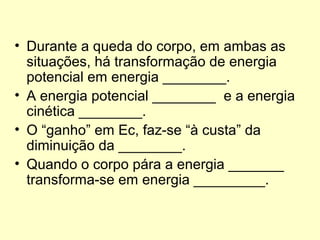
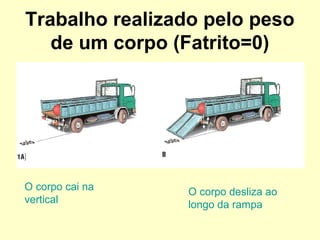
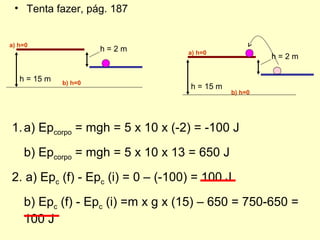
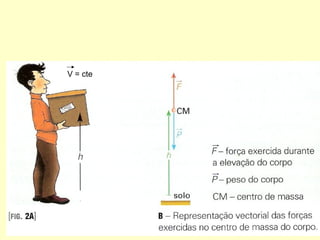
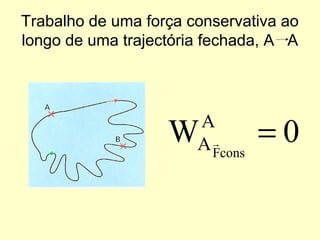
- O documento discute a conservação e transformação de energia mecânica em sistemas com forças conservativas e dissipativas. - Forças dissipativas como o atrito causam a diminuição da energia mecânica total do sistema. - A conservação da energia mecânica só se aplica quando as únicas forças são conservativas, como a gravidade.

1. Representação gráfica do trabalho realizado
por uma força constante.
Forças dissipativas. (p. 154-155;p. 167)
Teorema da energia cinética
Trabalho realizado pelo peso de um corpo.
Conservação da energia mecânica.

2. Relembrar:
Ec = ½ m v2
; ∆Ec = ½ m [(vf)2
-(vi)2
]
Ep = m g h ; ∆Ep = m g ∆h
Esist =Emec + Ei ; ∆Esist =∆Emec + ∆Ei ;

3. Não há trocas de Q
Não há trocas de m
Carro em movimento trava e pára,
vf = 0
Q
Sistema complexo – Com forças dissipativas
Emec = Ec + Ep
Esist = Emec + Ei
∆Emec<0 ; ∆Ei >0

4. A ação das forças dissipativas, traduz-se
numa diminuição da energia mecânica.
Diz-se que são forças não conservativas
(ex. forças de atrito)
A ação das forças dissipativas, traduz-se
numa diminuição da energia mecânica.
Diz-se que são forças não conservativas
(ex. forças de atrito)
∆Esist = 0
∆Esist = ∆Emec + ∆Eint =0
∆Emec<0 ;∆Ei>0
∆

5. No modelo do centro de massa a ação das
forças dissipativas traduz-se apenas numa
diminuição da energia mecânica.
Porquê? Pág. 167
No modelo do centro de massa a ação das
forças dissipativas traduz-se apenas numa
diminuição da energia mecânica.
Porquê? Pág. 167

6. Quando a ação das forças não fazem variar a
energia mecânica diz-se que são forças
conservativas (ex. peso de um corpo).
Quando a ação das forças não fazem variar a
energia mecânica diz-se que são forças
conservativas (ex. peso de um corpo).
Ex pág.175, nº20

7. Teorema da energia cinética
)(
2
1 22
ifF
F
vvmW
EcW
R
R
−=
∆=


TENTA FAZER pag. 178
Pág. 198, nº3 e 4

8. Trabalho realizado pelo peso
gravP
EpW ∆−=

9. Conservação da energia
mecânica
2211
21
EcEpEcEp
EmecEmec
+=+
=

10. • Durante a queda do corpo, em ambas as
situações, há transformação de energia
potencial em energia ________.
• A energia potencial ________ e a energia
cinética ________.
• O “ganho” em Ec, faz-se “à custa” da
diminuição da ________.
• Quando o corpo pára a energia _______
transforma-se em energia _________.

11. Trabalho realizado pelo peso
de um corpo (Fatrito=0)
O corpo cai na
vertical
O corpo desliza ao
longo da rampa

12. O trabalho realizado pelo peso de um corpo é
simétrico da variação da energia potencial do
sistema
WP = - ∆Ep
O trabalho realizado pelo peso do corpo
depende apenas do ponto inicial e do ponto
final e não da trajectória. Assim, diz-se que o
peso é uma força conservativa.
Uma força conservativa é uma força não
dissipativa
Pág. 192, nº 5

13. V = cte

14. WF=?
WF = F x h x cos0º
Como F = P = mg
WF = m x g x h
WP=?
WP = P x h x cos180º
WF = - m x g x h
WF+WP=WFR=?
WFR = 0 J
WFR = ∆Ec = 0 J

15. Trabalho de uma força conservativa ao
longo de uma trajectória fechada, A A
0WA
A consF
=

16. • Exercício resolvido, pág 187
• Tenta fazer, pág. 187
h = 2 m
h = 15 m

17. ∆Em = ∆Ei = 0
∆Em = 0
Eminício = Emfinal
∆Ei = 0
Conservação da energia mecânica
- forças de atrito desprezáveis-

18. Conservação da energia mecânica
Eminicio (2)= Emfim(4)

19. • Exercícios pág. 199, nº 8,9, 10, 13,14,17,
18, 19
Consultar síntese pág. 196

20. • Lição nº ___, ___, ___
Sumário: correcção do trabalho de casa.
Realização da actividade A.L. 2.3.
TPC
Ler a actividade A.L. 2.3, trazer máquina de
calcular e livro de lab.(pág. 56) PODE AJUDAR
A SUBIR A NOTA
Tenta fazer, pág. 187, nº2

21. • Tenta fazer, pág. 187
h = 2 m
h = 15 m
1.a) Epcorpo = mgh = 5 x 10 x (-2) = -100 J
b) Epcorpo = mgh = 5 x 10 x 13 = 650 J
2. a) Epc (f) - Epc (i) = 0 – (-100) = 100 J
b) Epc (f) - Epc (i) =m x g x (15) – 650 = 750-650 =
100 J
h = 2 m
h = 15 m
a) h=0
b) h=0
a) h=0
b) h=0

22. • Conclusão
Quando determino a variação de energia
potencial o referencial tomado como
referência (h=0), é arbitrário.

23. ∆Em = 0
Eminicio= Emfim
Eci + Epi = Ecf + Epf
Eci - Ecf = Epf – Epi
∆Ec + ∆Ep = 0
Conservação da energia mecânica
validade: qd só existem forças conservativas,
ex: peso

24. Eminicio= Emfim
∆Em = 0
Existem forças conservativas, ex. peso, e
forças não conservativas, ex. força de
atrito
∆Em = Edissipada
∆Ec + ∆Ep = Edissipada

25. Pág. 192 do manual, exercício resolvido
∆Ec + ∆Ep = Edissip
½ m (vf2
– vi2
) + mg(hf – hi) = Edissip
½ x 30 x 9 + 30 x 10 x (-2) = Edissip
15 x 9 – 600 = Edissip
Edissip = - 465 J
∆Em = Edissip <0 logo está a perder E. mecânica

26. ∆Em = Edissip
∆Ec + ∆Ep = 3/5 Em(i)
½ m(vf2
– vi2
) + mg(hf – hi) = 3/5 x (½ m vi2
+mghi)
Vf = 12 m/s
Pág. 193 do manual, tenta fazer
= 0
= 0 = 0

27. A.L. 2.3
∆Em = Edissip = WFatrito= Fatrito x ∆r x cosα
∆Em = Fatrito x ∆r
Fatrito
=
∆Em / ∆r
Fazer todos os registos no caderno / caderno de
actividades
Responder no caderno às questões da pág 62 do caderno
de actividades
?