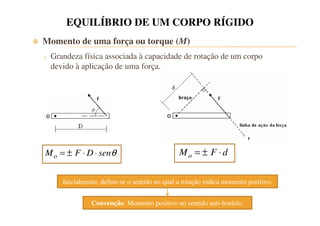
O documento discute o equilíbrio de estruturas, apresentando as condições de equilíbrio para pontos materiais e corpos rígidos em 1, 2 e 3 dimensões. Exemplos ilustram o cálculo de forças e momentos em sistemas sob equilíbrio, como determinar a tensão em cabos que sustentam um motor e calcular reações em barras e guindastes.

1. EQUILÍBRIO DE ESTRUTURAS
Prof. Magno Mota
Faculdade Área1
Disciplina: Resistência dos Materiais - 5REZN

2. EQUILÍBRIO DE UM PONTO MATERIAL
Condição de equilíbrio de um ponto material
o A resultante das forças que atuam sobre o ponto material deve ser
nula
F = 0
o É recomendada a construção do chamado diagrama de corpo livre.

3. EQUILÍBRIO DE UM PONTO MATERIAL
Equações de equilíbrio
o Para uma situação bidimensional
F x = 0
0 y F =
Onde 1 representa a componente da força 1 na direção do eixo x x F F
o Para uma situação tridimensional
1 2 3 4 0 x x x x F + F − F − F =
1 4 2 3 0 y y y y F + F − F − F =
0 z F =
0 x F = 0 y F =

4. EQUILÍBRIO DE UM PONTO MATERIAL
Exemplo 1
o Determinar a tensão nos cabos AB e AD para o equilíbrio do motor de
250 Kg mostrado na figura

5. EQUILÍBRIO DE UM CORPO RÍGIDO
Exemplo 2
o A figura abaixo um peso de 44 N suspenso no ponto P por uma corda.
Os trechos AP e BP da corda formam um ângulo de 90°, e o ângulo
entre BP e o teto é igual a 60°. Qual é o valor, em N, da tração no
trecho AP da corda?

6. EQUILÍBRIO DE UM CORPO RÍGIDO
Momento de uma força ou torque (M)
o Grandeza física associada à capacidade de rotação de um corpo
devido à aplicação de uma força.
o M = ± F ×D× senq
o M = ± F × d
Inicialmente, define-se o sentido no qual a rotação indica momento positivo.
Convenção: Momento positivo no sentido anti-horário.

7. EQUILÍBRIO DE UM CORPO RÍGIDO
Equações de equilíbrio de um corpo rígido
o Deve-se ter o equilíbrio de forças (evita a translação) e o equilíbrio de
momentos (evita a rotação):
Onde:
é a soma de todas as forças que F atual sobre o corpo
é a soma dos momentos de todas as forças em relação
a um pontor qualquer
o
O
M
=
0
=
o
0
F
M
o Para um problema bidimensional (forças atuando no plano x-y, com
origem no ponto O)
0 0 0 x y o F = F = M =
o Para um sistema de coordenadas tridimensional x, y, z com origem no
ponto O
0 0 0
0 0 0
= = =
F F F
M M M
x y z
= = =
x y z

8. EQUILÍBRIO DE UM CORPO RÍGIDO
Exemplo 3
o A lança AB do guindaste mostrado na figura abaixo possui massa
igual a 200 kg, está conectada por um pino em A e é sustentada pela
haste BC. Calcule a reação no apoio A e a força que atua na haste BC.

9. EQUILÍBRIO DE UM CORPO RÍGIDO
Exemplo 4
o Calcular as reações que atuam na barra abaixo. Desconsidere o peso
da barra.
Solução:
• Diagrama de corpo livre • Equações de equilíbrio
0 0
0 4 8 KN
= =
F R
x A
x
= =
F R ,
y A
y
0 12 48 KN
= = ×
M M , m
o A

10. EQUILÍBRIO DE UM CORPO RÍGIDO
Exemplo 5
o Calcular as reações que atuam na estrutura abaixo. A estrutura possui
massa igual a 200 Kg, é constituída por um único material e apresenta
a mesma seção transversal em todos os pontos.