Mca3 resol.cap5

|1|

MATEMÁTICA CIÊNCIA E APLICAÇÕES 3

Números complexos

5.

5

a) i25 · i18 = i43 = i3 = i2 · i = –i
b) (–2i)11 = (–2)11 · i11 = – 2 048 · i3 = – 2 048 (–i) = 2 048 i
i79
= i47 = i3 = –i
i32
0 2
d) [(i2)2 ]3 = [(i2)1]9 = i18 = i2 = –1
i–98
e) –34 = i–64 = (i64)–1 = (i0)–1 = 1
i
c)

Exercícios
1.

a) (3, 2) + (0, 1) = (3 + 0, 2 + 1) = (3, 3)

b) (2, 3) · (– 1, 4) = (2 · (–1) – 3 · 4, 2 · 4 + 3 · (–1)) = (–14, 5)
c) (2x – y, 6x + 2y) + (x – 2y, x) = (2x – y + x – 2y,

f )

6x + 2y + x) = (3x – 3y, 7x +2y)
d) (–1, –1) · (– 4, 2) = ((–1) · (–4) – (–1) · 2, (–1) · 2 +
+ (–1) (–4)) = (6, 2)

6.

i + i2 + i3 + i4 = i – 1 – i + 1 = 0
i = i5 = i9 = ... = i49 = i
i2 = i6 = i10 = ... = i50 = –1
⇒
i3 = i7 = i11 = ... = i47 = –i
i4 = i8 = i12 = ... = i48 = 1

e) (2, –3) – (–1, –2) = (2 – (–1), (–3) – (–2)) = (3, –1)
f ) (1, 0) · (x, –y) = (1, x – 0 · (–y), 1 · (–y) + 0 · x) = (x, –y)

2.

0
1
1 + i
i132 + i61
= 1 – i.
= i + i =
–1
i42
i2

z1 = (–2, 1), z2 = (0, –1)

⇒ (i + i2 + i3 + i4) + (i5 + i6 + i7 + i8) + ... +
= 0

z1 + z2 = (–2, 1) + (0, –1) = (–2, 0)

+ (i45 + i46 + i47 + i48) + i49 + i50 = i – 1

z1 · z2 = (–2, 1) · (0, –1) = (–2 · 0 – 1 · (–1), (–2)(–1) + 1 · 0) =

= 0

= (1, 2)
Im(z)

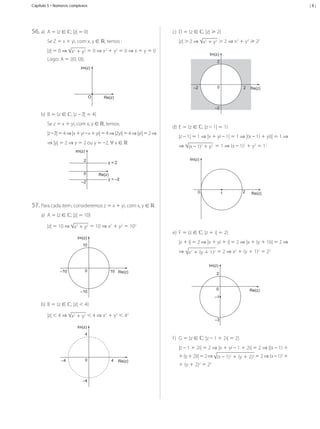
7.
Q

2
M

1

–2 P

1

= 0

a)

i
i5
i9
i13

i2
i6
i10
i14

i3
i7
i11
i15

i4
i8 ⇔
i12
i16

i

–1 –i

1

i

–1 –i

1

i

–1 –i

1

i

–1 –i

1

O quadrado não é mágico, pois as somas dos elementos

Re(z)

das colunas não são iguais.

–1 N

b) S = 4i + 4 (–1) + 4 (–i) + 4 · 1 = 0

3.

z1 = (x, 3) e z2 = (2 – y, y)

8.

z2 – z1 = (5, –4) ⇒ (2 – y, y) – (x, 3) = (5, –4) ⇒
⇒ (2 – y – x, y – 3) = (5, 4) ⇒

2 – y –x = 5
y – 3 = –4

b) (–4, 3) = –4 + 3i
c) 1 – 2i = (1, –2)

⇒

d) 5i = (0, 5)

⇒ x = –2 e y = – 1

4.

a) (3, –2) = 3 – 2i

e) (0, 4) = 4i
f ) (4, 0) = 4

a) i54 = i2 = –1

g) –3 + i = (–3, 1)

b) i = i = i · i = (–1) · i = –i

h) –5 = (–5, 0)

95

3

2

c) i = i = i
161

1

9.

d) i200 = i0 = 1
e) i

= i =i

f ) i

= i2 =1

1 221

1

b) z = 3i + 3 ⇒ Re(z) = 3 e Im(z) = 3

2 022

g) i
h) i

= i = i · i = –i

13 335

3

= i0 =1

12 784

MCA3-ManualResoluções-2aProva.indd 90

a) z = 4 + 5i ⇒ Re(z) = 4 e Im(z) = 5

2

c) z = – 1 + 1 i ⇒ Re(z) = – 1 e Im(z) = 1
4
2
4
2
d) z = –7 – i ⇒ Re(z) = –7 e Im(z) = –1

13/05/10 04:33

Capítulo 5 • Números complexos

|2|

–2 + 5i
= – 2 + 5 i ⇒
3
3
3
2 e Im(z) = 5
⇒ Re(z) = –
3
3

c) Re(z) > Im(z) ⇒ 3 – x > x + 1 ⇒ x < 1

e) z =

d) Im(z) < 3 ⇒ x + 1 < 3 ⇒ x < 2

f ) z = –i 3 ⇒ Re(z) = 0 e Im(z) = – 3

17. a) m + (n – 1)i = –4 + 3i ⇒
10. z = (1 + 2i) · (i – 4) = i – 4 + 2i2 – 8i i = –1 z = – 6 – 7i ⇒

m = –4
e
n –1 = 3 ⇒ n = 4

2

⇒ M = (–6, –7)

11. a) z = (m – 3) + 4i é imaginário puro ⇔ Re(z) = m – 3 =
= 0 e Im(z) = 4 ≠ 0 ⇔ m = 3
b) z = –3 + (m + 3)i é real ⇔ Im(z) = m + 3 = 0 ⇔ m =
= –3

n – 2 = 3 ⇒ n = 5
b) (n – 2, m + 5) = (3, –2) ⇒ e
m + 5 = – 2 ⇒ m = –7
m – 3 = 0 ⇒ m = 3
c) (m – 3) = (n – 2)i = 5i ⇒ e
n – 2 = 5 ⇒ n = 7
d) (m – n + 1) + (2m + n – 4)i = 0 ⇒

12. - z = (1 – p) + (p – 1)i é real ⇒ Im(z) = p – 1 = 0 ⇒
2

⇒ p = –1 ou p = –1

2

z ≠ 0

p = –1

⇒

--p = –1 ⇒ z = 1 + 1 = 2

m = 1 e n = 2

18. a) (2 – 3i) + (–1 + 2i) + (3 + 2i) = (2 – 1 + 3 ) +

13. z = (m2 – 25) + (m + 5)i

+ (– 3 + 2 + 2)i = 4 + i

a) z é imaginário puro ⇒

Re(z) = m – 25 = 0 ⇒ m = 5 ou m = –5
⇒ e

b) (–7 + 5i) – (3 – 2i) = –7 + 5i – 3 + 2i = – 10 + 7i

2

⇒ m = 5

Im(z) = m + 5 ≠ 0 ⇒ m ≠ – 5

m – n + 1 = 0
e
2m + n – 4 = 0

c) 2 + (3 – i) + (–1 + 2i) + i = 2 + 3 – i – 1 + 2i + i =
= 4 + 2i
d) 4i – (1 – 3i) – (–2 + i) = 4i – 1 + 3i + 2 – i = 1 + 6i

b) m = 5 ⇒ z = (52 – 25) + (5 + 5)i ⇒ z = 10i

e) (–4 + 3i) + 2i – (–3 – i) = –4 + 3i + 2i + 3 + i = – 1 + 6i
f ) –1 – (–2 + i) + (5 – i) – (3 – 7i) = –1 + 2 – i + 5 – i –

14. z = (m2 + 1) + (m – 1)i é imaginário puro ⇒

Re(z) = m2 – 1 = 0 (∃ m ∈ ℝ
/
⇒ e
Im(z) = m – 1 ≠ 0 ⇒ m ≠ 1

⇒ ∃ m ∈ ℝ
/

15. v = (–2 – m) + 3ni é imaginário puro ⇒
(1) – 2 – m = 0 ⇒ m = –2
⇒ e
(2) 3n ≠ 0 ⇒ n ≠ 0
w = 4 – (m2 – 4)i é real ⇒ m2 – 4 = 0 ⇒ m = 2 ou
m = –2 (3)

– 3 + 7i = 3 + 5i

19. u = 2 + 3i, v = – 5i e w = –1 – 2i
a) u + v + w = 2 + 3i – 5i – 1 – 2i = 1 – 4i
b) (u – i) + (v – w) = 2 + 3i – i – 5i + 1 + 2i = 3 – i
c) v – w + u = – 5i + 1 + 2i + 2 + 3i = 3

20. a) z1 = (–2, x) = – 2 + xi, com x ∈ ℝ e z2 = (y, – 3) =
= y – 3i, com y ∈ ℝ
b) z1 + z2 = – 4 + 2i ⇒ – 2 + xi + y – 3i = – 4 + 2i ⇒
⇒ (y – 2) + (x – 3)i = – 4 + 2i ⇒

Como m = –2 satisfaz (1) e (3), então m = –2.
Logo: m = –2 e n ≠ 0

y – 2 = –4
⇒

16. z = (3 – x) + (x –1)i
a) Re(z) = 2 ⇒ 3 – x = 2 ⇒ x = 1
b) Im(z) = –4 ⇒ x + 1 = –4 ⇒ x = –5


21.

e
x – 3 = 2

x = 5 e y = –2

u + v = 2 – 5i (1)
u – 2 v = –4 + 13 (2)

13/05/10 04:33

|3|


Subtraindo-se membro a membro: (2) de (1), vem: 3v =

25. a) Fazendo-se

–5 + 12i = x + yi, com x, y ∈ ℝ, vem:

= 6 – 18 i ⇒ v = 2 – 6i (3).

( –5 + 12i) = (x + yi)2 ⇒ –5 + 12i = (x2 – y2) +

Substituindo-se (3) em (1): u + 2 – 6i = 2 – 5i ⇒ u = i.

+ 2xyi ⇒ 2xy = 12 ⇒ y = 6 (2)

2

22. a) x2 + 100 = 0 ⇒ x2 = –100 ⇒ x = 100 · (–1) =

x2 – y2 = –5 (1)

Substituindo-se (2) em (1): x2 – 36 = –5 ⇒
2

x
⇒ (x2)2 + 5x2 – 36 = 0 ⇒ x2 = 4 ou x2 = –9 (x ∈ ℝ) ⇒

=100i2 ⇒ x = 10i ou x = –10i

⇒ x = 2 ou x = –2.

b) x2 – 6x + 10 = 0
6 ± 2i
6 ± 4i2
⇒ x =
=
2
2 ⇒
2
∆ = – 4 = 4i

x = 2 (2) y = 3
x = –2 (2) y = –3

⇒ x = 3 + i ou x = 3 – i

c) –x2 + 4x – 29 = 0 ⇒

x2 – 4x + 29 = 0
∆ = –100 = 100i2

⇒ x =

x2 – y2 = 0 (1)
⇒ e
2xy = 4 ⇒ y = 2 (2)
x

d) (x2 + 9) · (x2 – 1) = 0 ⇒
x2 + 9 = 0 ⇒ x2 = –9 = 9i2 ⇒ x = 3i ou x = –3i
⇒ ou

Substituindo-se (2) em (1): x2 – 42 = 0 ⇒ x4 – 4 =
= 0 ⇒ (x2 – 2)(x2 + 2) = 0

23. x3 – 14x2 + 58x = 0 ⇒ x ( x2 – 14x + 58) = 0 ⇒
(I) x = 0
ou
(II) x2 – 14x + 58 = 0

∆ = –36

não existe x ∈ ℝ

x = 2 (2) y = 2

( 4 + 3i)2 = (x + yi)2 ⇒ 4 + 3i = (x2 – y2) + 2xyi ⇒

24. a) x + 5x + 6 = 0 ⇒ (x + 2)(x + 3) = 0 ⇒
2

2

2

x = – 2 = 2i ⇒ x = i 2 ou x = – i 2
ou
x2 = –3= 3i2 ⇒ x = i 3 ou x = –i 3
2

Logo: S = {i 2 , – i 2 , i 3 , –i 3 }

b) x4 + 3x2 – 4 = 0 ⇒ (x2)2 + 3x2 – 4 = 0 2 y2 +
x = y
+ 3y – 4 = 0 ⇒ y = 1 ou y = –4 ⇒
⇒

x2 = 1 ⇒ x = 1 ou x = –1
ou
x2 = –4 = 4i2 ⇒ x = 2i ou x = – 2i

Logo: S = {–1,1, –2i, 2i}.


x2 – y2 = 4 (1)
2xy = 3 ⇒ y = 3 (2)
2x

2
(II): x2 – 14 x + 58 = 0 ⇒ x = 14 ± 36 i =
2
= 14 ± 6 i ⇒ x = 7 + 3i ou x = 7 – 3i
2
Logo: S = {0, 7 + 3i, 7 – 3i}.

⇒

2 + i 2
– 2 – i 2

c) Fazendo-se 4 + 3i = x + yi, com x, y ∈ ℝ, vem:

⇒

(I): 0 ∈ ℂ

2

⇒ 4i =

x = – 2 ⇒ y = – 2

a) Universo ℝ: S = {0}
b) Universo ℂ:

x ∈ ℝ

x
x2 = 2 ⇒ x = 2

ou x = – 2

x2 – 1 = 0 ⇒ x2 = 1 ⇒ x = 1 ou x = –1

4

2 + 3i
–2 – 3i

( 4i)2 = (x + yi)2 ⇒ 4i = (x2 – y2) + 2xyi ⇒

x = 2 – 5i

⇒

⇒ –5 + 12i =

b) Fazendo-se 4i = x + yi, com x, y ∈ ℝ, vem:

2
= 4 ± 100 i = 4 ± 10i ⇒ x = 2 + 5i ou
2
2

x

Substituindo-se (2) em (1):
x2 – 9 2 = 4 ⇒ 4(x2)2 – 16x2 – 9 = 0 ⇒ x2 = 18 ou
4x
4
2 (x ∈ ℝ) ⇒ x = 3 2 ou x = – 3 2
x2 = –
2
2
4
x = 3

2

2

x = – 3

2

(2) y =
2

2
2

(2) y = –

⇒ 4 + 3i =
2
2

3 2 + i 2
2
2
=
3 2 – i 2
–
2
2
d) Fazendo-se 1 – i 3 = x + yi, com x, y ∈ ℝ, vem:

( 1 – i 3 )2 = (x + yi)2 ⇒ 1 – i 3 = (x2 – y2) + 2xyi ⇒
⇒

x2 – y2 = 1 (1)
3
(2)
2xy = – 3 ⇒ x = –
2y

13/05/10 04:33


|4|

3 2 – y2 = 1 ⇒ 4 (y2)2 + 4y2 – 3 = 0 ⇒ y2 = – 6 (y ∈ ℝ)

4y
4
2
2
ou y = –
ou y2 = 2 ⇒ y =
2
2
4
y =

2
6
x = –
2 (2)
2

⇒

6
2
– + i
2
2
=
6 2
– i
2 2

2
6
y = – (2) x =
2
2

30. z1 =

1 , 3 = 1 + 3i; z = (2, –5) = 2 – 5i
2
2
2

a) z1 · z2 = 1 + 3i (2 – 5i) = 1 – 5 i + 6i – 15i2 = 16 +
2
2
+ 7 · i
2
b) z2 = (2 – 5i)2 = 4 – 20i + 25i2 = –21 – 20i
2

1 – i 3 =

31. a) (1 + i)5 · (1 – i)5 = [(1 + i) (1 – i)]5 = (1 – i2)5 = 25 = 32
b) (1 – i)3 = (1 – i) (1 – i)2 = (1 – i) (1 – 2i + i2) =
= (1 – i) (–2i) = –2i + 2i2 = –2 – 2i
c) (2 + 2i)4 = [(2 + 2i)2]2 = (4 + 8i + 4i2)2 = (8i)2 = 64i2 =
= –64

26. a) (2 + 5i) (1 – i) = 2 – 2i + 5i – 5i2 = 2 + 3i – 5 (–1) = 7 + 3i
b) (4 + 3i)(–2 + 2i) = – 8 + 8i – 6i +6i2 = –14 + 2i
c) (6 – 3i) (–3 + 6i) = – 18 + 36i + 9i – 18i2 = 45i
d) (4 + i ) (2 – i) + 3 – i = 8 – 4i + 2i – i2 + 3 – i =
= 12 – 3i

32. z = (a + i)3, em que a ∈ ℝ
a) z = (a + 1)3 = a3 + 3a2i + 3ai2 + i3 = (a3 – 3a) + (3a2 – 1)i

b) z é imaginário puro ⇒
a3 – 3a = 0 ⇒ a (a2 – 3) = 0 ⇒ a = 0, a = 3

e) 4 + 3i + (1 – 2i) (3 + i) = 4 + 3i + 3 + i – 6i – 2i2 =
= 9 – 2i
f ) (–5i) (4 – 3i) (1 + 2i) = (–5i) (4 + 8i – 3i – 6i2) =
= (–5i) (10 + 5i) = –50i – 25i2 = 25 – 50i

3
⇒ ou a = – (1)
e
3a2 – 1 ≠ 0 (2)
Como todos os valores de a encontrados em (1) satisfazem (2), então: a = 0, a = 3 ou a = – 3 .

27. a) (1 + i) · (1 – i) = 1 – i = 2
2

b) (2 – 3i)2 = 4 – 12i + 9i2 = –5 – 12i
c) (4 + i)2 = 16 + 8i + i2 = 15 + 8i
d) (–3 – 3i)2 = [–(3 + 3i)]2 = (3 + 3i)2 = 9 + 18i + 9i2 = 18i
e) (4 + 4i)3 = 43 + 3 · 42 · 4i + 3 · 4 · (4i)2 + (4i)3 = 64 +
+ 192i + 192i2 + 64i3 = 64 + 192i – 192 – 64i = –128 +
+ 128i
f ) (2 + i)3 = 23 + 3 · 22 · i + 3 · 2 · i2 + i3 = 8 + 12i – 6 – i =
= 2 + 11i

28. u = 4 – 3i, v = –5i e w = 1 + 2i

33. - z = (x + 3i) · (1 – 2i) = x – 2xi + 3i – 6i2 = (x + 6) +
+ (3 – 2x)i, com x ∈ 

--z ∈  ⇒ 3 – 2x = 0 ⇒ x = 3
2
3 ⇒ z = 3 + 6 ⇒ z = 15
--x = 2
2
2

34. - z = (x + i) (x + 2i) = x2 + 2xi + xi + 2i2 = (x2 – 2) + 3xi,
com x ∈ 

--z é imaginário puro ⇒

x2 – 2 = 0 ⇒ x = 2 ou x = – 2 (1)
⇒ e
3x ≠ 0 (2)

u · v · w = (4 – 3i) · (–5i) (1 + 2i) = (4 – 3i) (–5i – 10i2) =

Como todos os valores de x encontrados em (1) satisfa-

= (4 – 3i) (–5i + 10) = – 20i + 40 + 15i2 – 30i = 25 – 50i

zem (2), então x = 2 ou x = – 2 .

29.

2

3 ( 3 + i 3 ) = 3( 3 + i 3 )2 = 3(3 + 6i + 3i2) =

--Assim :

x = 2 ⇒ z = 3 2 i
x = – 2 ⇒ z = –3 2 i

= 3(6i) = 18i


13/05/10 04:33

|5|


35. u = – 2 + i ⇒ A = (–2, 1)

b)
Im(z)

v = 1 + 5i ⇒ B = (1, 5)
P

7

–4

w = 4 + i ⇒ C = (4, 1)

0

AABC = 1 · AC · BH = 1 · 6 · 4 = 12
2
2
Im (z)
B

5

A

H

–2

1

0

4

Re(z)

C
4

–7

P'
P = (–4, 7) ⇒ P' = (4, –7)

Re (z)

c)

36. z1 = –1 – 3i, z2 = 2i e z3 = 1 – i

Im(z)
P

b) z2 · z3 = 2i (1 – i) = 2i · (1 + i) = 2i + 2i2 = – 2 + 2i
= –2i
c) z1 + z3 = –1 – 3i + 1 – i = –1 + 3i + 1 – i = 2i

0

a) z1 + z2 = – 1 – 3i + 2i = 1 – 3i – 2i = 1 – 5i

7

–4

d) Usando as propriedades do conjugado:
z2 · z3 = z2 · z3 = z2 · z3 = (–2 i) · (1 – i) =

Re(z)

= –2i + 2i2 = –2 –2i

37. P = (2, –3) ⇒ z1 = 2 – 3i; Q = (–1, 2) ⇒ z2 = –1 + 2i
a) z1 = 2 + 3i ⇒ afixo: (2, 3)
b) z1 · z2 = (2 – 3i) (–1 – 2i) = –2 – 4i + 3i + 6i2 = – 8 – i ⇒
⇒ afixo: (–8, –1)

–7
P'
P = (–4, 7) ⇒ P' = (–4, –7)

d) P = (–4, 7) ⇒ z = –4 + 7i
zi = (–4 + 7i) · i = – 4i + 7i2 = –7 – 4i ⇒ P' = (–7, –4)

c) (z 1 · z 2 ) = z · z = (2 + 3i) · (–1 + 2i) =
2

2
1

2
2

2

2

= (4 + 12i + 9i2) (1 – 4i + 4i2) = (–5 + 12i) (–3 – 4i) =
= 15 + 20i – 36i – 48i2 = 63 – 16i ⇒ afixo: (63, –13)

39. Seja z = a + bi, com a, b ∈ .
z – z = 6i ⇒ (a + bi) – (a – bi) = 6i ⇒ 2bi = 6i ⇒
⇒ b = 3, ∀a ∈ 

38. a)

Logo: z = a + 3i, em que a ∈ .
Im(z)
P

7

P'

40. Seja z = a + bi, com a, b ∈ .
2 · zi + 3 = 2z – z + 2i ⇒ 2i (a – bi) + 3 =
= 2 (a + bi) – (a – bi) + 2i ⇒

–4

0

⇒ (2b + 3) + 2ai = a + (3b + 2)i ⇒
4 Re(z)

P = (–4, 7) ⇒ P' = (4, 7)

⇒ 2b + 3 = a
2a = 3b + 2
Logo: z = –5 – 4i.


⇒ a = –5 e b = – 4


41. a) (z)2 = z
Seja z = a + bi, com a, b ∈ , temos:
(a – bi)2 = (a + bi)2 ⇒ a2 – b2 – 2abi = a2 – b2 + 2abi ⇒
⇒

(1) a2 – b2 = a2 – b2 ⇒ ∀a, b, ∈ 
(2) – 2ab = 2ab ⇒ a · b = 0 ⇒ a = ou b = 0

De (1) e (2), conclui-se que a = 0 ou b = 0, ou seja:
z é um número real ou um imaginário puro.
b) z2 = 2 · z · i
Seja z = a + bi, em que a, b ∈ , temos:

|6|

1
3 + i
3 + i
3
1
c) 3 – i = (3 – i)(3 + i) = 9 – i2 = 10 + 10 · i
2i
2i(1 + i)
2i + 2i2
–2 + 2i
d) 1 – i = (1 – i)(1 + i) = 1 – i2 =
= –1 + i
2
2
2
e) 4 + i = (4 + i) = 16 + 8i + i = 15 + 8i =
(4 – i)(4 + i)
16 – i2
4 – i
17
= 15 + 8 i
17 17

f ) 6 = 6 · i2 = 6i = – 6 i
5i
5 · i
–5
5

z2 = 2 · z · i ⇒ (a + bi)2 = 2i (a – bi) ⇒
⇒ a2 – b2 + 2abi = 2b + 2ai ⇒
2
2
⇒ a – b = 2b (1)
ab = a (2)

De (2): ab = a ⇒ a(b – 1) = 0 ⇒ a = 0 ou b = 1
a = 0 (1) –b2 = 2b ⇒ b (b + 2) = 0 ⇒ b = 0
ou b = – 2
b = 1 ⇒ a2 –1 = 2 ⇒ a = 3 ou a = – 3
Assim temos:
a = b = 0 ⇒ z = 0
a = 0 e b = – 2 ⇒ z = – 2i
a = 3 e b = 1 ⇒ z = 3 + i
a = – 3 e b = 1 ⇒ z = – 3 + i
c) (z)2 = –2i
Seja z – a + bi, com a, b ∈ , temos:
(z)2 = – 2i ⇒ (a – bi)2 = –2i ⇒ a2 – b2 – 2abi = – 2i ⇒

⇒

a – b = 0 (1)
ab = 1 (2)
2

2

De (1): a2 – b2 = 0 ⇒ (a – b) · (a + b) = 0 ⇒
⇒ a = b ou a = – b
a = b (2) a2 = 1 ⇒ a = b = 1 ou a = b = – 1
a = – b (2) – a2 = 1 ⇒ a2 = –1 ⇒ ∃ a, b ∈ 
/

Assim:

42. a)

a = b = 1 ⇒ z = 1 + i
a = b = –1 ⇒ z = –1 –i

3 – 7i = (3 – 7i)(3 – 4i) = 9 – 12i – 21i + 28i2 =
9 – 16i2
3 + 4i
(3 + 4i)(3 – 4i)
19
33
= –19 – 33i = – 25 – 25 i
25

1 – i
1
– i
1 – i
43. a) z = 1 + 1 + i = i(–i) + (1 + i)(1 – i) = –i + 1 – i2 =
i
= –i + 1 – i = –2i + 1 – i = 1 – 3 i
2
2
2 2
b) z =

3 – 2i = 3(2 – 3i) – 2i (3 + 2i) =
2 + 3i 3 – 2i
4 – 9i2
9 – 4i2

2
= 6 – 9i – 6i – 4i = 10 – 15 i
13 13
13
c) z = 1 + i – i = (1 – i)(–i) – i(1 – i) = –i +
i
1 + i
i(–i)
1 – i2
2
+ i2 – i + i = –2i – 2 – i –1 = – 3 – 3 i
2
2
2 2

d) z = 2 – i + 1 – 2i = (2 – i)(3 + i) + (1 – 2i)(3 – i) =
3 – i
3 + i
(3 – i) (3 + i)
=

6 – i – i2 + 3 – 7i + 2i2
4 4
= 5 – 5 i
9 – i2

2
e) z = (2 – i)(4 + 3i) = 8 + 6i – 4i – 3i = 11 – 2i =
1 – 2i
1 – 2i
1 – 2i

=

(11 + 2i)(1 + 2i) 11 + 22i + 2i + 4i2
7
24
=
= 5 + 5 i
5
1 – 4i2

2
2
f ) z = (1 + i) = 1 + 2i + i = 2i = 2i (1 + i) =
1 – i
1 – i
1 – i
12 – i2

= –2 + 2i = –1 + i
2

44. z = 3 – 4i
3 + 4i
a) 1 = 1 =
= 3 + 4i = 3 + 4 i
z
3 – 4i (3 – 4i)(3 + 4i) 9 – 16i2 25 25
1 =
1
1 =
=
b) z1 = 12 =
z
(3 – 4i)2
9 – 24i + 16i2
–7 – 24i
= –7 + 24i 2 = – 7 + 24 i = z1 = – 7 – 24 i
49 – 576 i
625 625
625 625
1
c) 1 =
= 1 = 4 – 3i 2 = 4 – 3 i
zi
(3 – 4i) · i
4 + 3i
16 – 9i
25 25

2
b) 1 – 2i = (1 – 2i)(2 – i) = 2 – i – 4i + 2i = –5i = – i
4 – i2
2 + i
(2 + i)(2 – i)
5


13/05/10 04:33

|7|


45. z =

1
1 + i

e) z = – 2 3 – 2i ⇒ |z| = (–2 3 )2 + (–2)2 = 4

a) 1 = 1 + i
z
1
= 1 = –i = – 1 i ⇒
b) z2 = 1 2 =
(1 + i)
1 + 2i + i2
2i
2
2i(–i)
1
⇒ Re(z2) = 0 e Im(z2) = –
2

46. 3 + 2i = 1 – i ⇒ z = 3 + 2i =
z
1 – i

1 1
f ) z = – ⇒ |z| =
4 4

51. |2 + 3i| =

2

4 + 9 = 13 ≅ 3,61; |3 + i| = 9 + 1 =

= 10 ≅ 3,16; |1| = 1
1
1
1
|–2| = 2; |4i| = 16 = 4; |– i| = 4 =
2
2

(3 + 2i)(1 + i) =
(1 – i)(1 + i)

2
= 3 + 3i + 2i + 2i ⇒ z = 1 + 5 i
1 – i2
2 2

2

2
1 + – 1
=
4
4
4

Logo, o complexo que tem o maior módulo é 4i.

52. a) z = (2 – 3i) · (4 + 6i) ⇒ |z| = |2 –3i| · |4 + 6i| =

4 + 9 ·

· 16 + 36 = 13 · 52 = 26
2
2 + i
47. z = 3 – ai = (2 + i)(3 + ai) = 6 + 2ai + 3i + ai ⇒
9 + a2
9 – a2 i2

|3i|
2
= 3 = 3 = 3
b) z = 3i ⇒ |z| =
|1 + i|
1 + i
2
2
1 + 1

⇒ z = 6 – a2 + 2a + 3 · i
9 + a
9 + a2

c) z = 2 · i119 = 2i3 = – 2i ⇒ |z| = |–2| = 2

z: imaginário puro ⇒

Logo: a = 6, pois este valor satisfaz a condição (2).

48. z = 2 + mi = (2 + mi)(1 + i) = 2 + 2i + mi + mi ⇒
1 – i2
1 – i
(1 – i)(1 + i)
2

⇒ z = 2 – m + 2 + m · i (1)
2
2

51

53
51
2
49. (1 + i)51 = (1 + i) · (1 + i) = 1 + i · (1 + 2i +i2) =
51
1 – i
(1 – i)
(1 – i)
51

2i
· (2i) = 1 – i2

f ) z =
=

|5i|
5i
⇒ |z| =
=
( 3 – i) (3 + 4 i)
| 3 – i| |3 + 4 i|
5
= 5 = 1
2 · 5
2
3 + 1 · 9 + 16

53. u = 2 + i, v = 3 – 2i e w = i

--z ∈ ℝ ⇒ 2 + m = 0 ⇒ m = –2
2
--Substituindo-se m = –2 em (1), obtém-se z = 2.

(1 + i)2
= (1 – i) (1 +i)

e) z = (4 – 4i) (1 – i) = (4 + 4i) (1 – i) ⇒ |z| = |4 + 4i| ·
· |1 – i| = 16 + 16 · 1 + 1 = 4 2 · 2 = 8

(1) 6 – a2 = 0 ⇒ a = 6
⇒ e 9 + a
(2) 2a + 3 ≠ 0
9 + a2

d) z = 2i (–1 + 2i) = –2i + 4i2 = – 4 – 2i ⇒
⇒ |z| = 16 + 4 = 2 5

51

· (2i) =

2i 51
= 2 · (2i) = i51 · (2i) = i3 · (2i) = 2i4 = 2 ∈ 

v – u · w = 3 – 2i – (2 + i)i = 3 – 2i – 2i – i2 = 4 – 4i ⇒
⇒ |v – u · w| = |4 – 4i| = 16 + 16 = 4 2

54. z1 = x + 3i e z2 = 2 + (x – 1)i, com x ∈ 
|z1| = |z2| ⇒ x2 + 9 = 4 + (x – 1)2 ⇒
⇒ x2 + 9 = 4 + x2 – 2x + 1 ⇒ x = –2

55. A = (3, 1) ⇒ z1 = 3 + i; B = (2, –2) ⇒ z2 = 2 – 2i
a) z1 + z2 = (3 + i) + (2 – 2i) = 5 – i ⇒ |z1 + z2| =
= 25 + 1 = 26

50. a) z = 2 + i ⇒ |z| =

22 + 12 = 5

b) z = 5i ⇒ |z| = 02 + 52 = 5
c) z = –4 + 3i ⇒ |z| = (–4)2 + 32 = 5
d) z = –4 ⇒ |z| = |–4| = 4


b) z1 – z2 = (3 + i) – (2 – 2i) = 1 + 3i ⇒ |z1 – z2| =
= 1 + 9 = 10
c) z1 · z2 = (3 – i) (2 + 2i) = 8 + 4i ⇒ |z1 · z2 | = 64 + 16 =
= 4 5

13/05/10 04:33


|8|

56. a) A = {z ∈ ℂ; |z| = 0}

c) D = {z ∈ ℂ; |z| ⩾ 2}

Se Z = x + yi, com x, y ∈ ℝ, temos :

|z| > 2 ⇒ x2 + y2 > 2 ⇒ x2 + y2 ⩾ 22

|z| = 0 ⇒ x2 + y2 = 0 ⇒ x2 + y2 = 0 ⇒ x = y = 0
Logo: A = {(0, 0)}.

Im(z)
2

Im(z)

–2
O

0

2

Re(z)

Re(z)
–2

b) B = {z ∈ ℂ; |z – z| = 4}
Se z = x + yi, com x, y ∈ ℝ, temos:
|z – z| = 4 ⇒ |x + yi – x + yi| = 4 ⇒ |2yi| = 4 ⇒ |yi| = 2 ⇒
⇒ |y| = 2 ⇒ y = 2 ou y = –2, ∀ x ∈ ℝ
Im(z)
2
0
–2

d) E = {z ∈ ℂ; |z – 1| = 1}
|z – 1| = 1 ⇒ |x + yi – 1| = 1 ⇒ |(x – 1) + yi)| = 1 ⇒
⇒ (x – 1)2 + y2 = 1 ⇒ (x – 1)2 + y2 = 12
Im(z)

y=2
Re(z)
y = –2

0

1

2

Re(z)

57. Para cada item, consideremos z = x + yi, com x, y ∈ ℝ.
a) A = {z ∈ ℂ; |z| = 10}
|z| = 10 ⇒ x2 + y2 = 10 ⇒ x2 + y2 = 102
Im(z)

e) F = {z ∈ ℂ; |z + i| = 2}
|z + i| = 2 ⇒ |x + yi + i| = 2 ⇒ |x + (y + 1)i| = 2 ⇒

10

⇒ x2 + (y + 1)2 = 2 ⇒ x2 + (y + 1)2 = 22
Im(z)
–10

0

10 Re(z)

2

0

–10

Re(z)

–1

b) B = {z ∈ ℂ; |z| < 4}
|z| < 4 ⇒ x2 + y2 < 4 ⇒ x2 + y2 < 42

–3

Im(z)
4

f ) G = {z ∈ ℂ; |z – 1 + 2i| = 2}
|z – 1 + 2i| = 2 ⇒ |x + yi – 1 + 2i| = 2 ⇒ |(x – 1) +

–4

0

4

Re(z)

+ (y + 2)i| = 2 ⇒ (x – 1)2 + (y + 2)2 = 2 ⇒ (x – 1)2 +
+ (y + 2)2 = 22

–4


13/05/10 04:33

|9|


g) z = –3 – 3i 3 ⇒ |z| = 9 + 9 · 3 = 6

Im(z)

1

–1

3
= – 1
6
2
3 3 = – 3
sen θ = –
6
2
cos θ = –

3 Re(z)

–2

⇒

3π
π < θ < 2

θ = π + π =
3
4π
=
3

h) z = 2 + i 2 ⇒ |z| = 2 + 2 = 2
2
2
2
sen θ =
2
cos θ =

58. a) z =

3 + i ⇒ |z| = 3 + 1 = 2
⇒

0° < θ < 90°

θ = 30°

z é um número real e Re(z) < 0 ⇒ θ = π
j) z = 6 – i 2 ⇒ |z| = 6 + 2 = 2 2

b) z = 4 3 – 4i ⇒ |z| = 16 · 3 + 16 = 8
3
8
2
4
1
sen θ = – 8 = – 2
3

sen θ =

2

=

= –

2 2
2
2
=
2
2 2

⇒

270° < θ < 360°

θ = 360° – 30° =
= 330°

k) z = –

2
2

⇒

90° < θ < 180°

θ = 180° – 45° =
= 135°

2
= – 1
4
2
2 3 = 3
sen θ =

4
2
cos θ = –

⇒

90° < θ < 180°

θ = 180° – 60° =
= 120°

2
e) z = – 1 – 1 i ⇒ |z| = 1 + 1 =
4
4
2 2
2

cos θ =

sen θ =

2
2
1
– 2

2
2

θ = 2π – π = 11π
6
6

– 2
2
cos θ =
= – 1
2
2

⇒

π
2 < θ < π

6
2
3
=
2
2

θ = π – π = 2π
3
3

l) z = – i
4
z é imaginário puro e IM(z) < 0 ⇒ θ = 3π
2

59. P1∈ semieixo real positivo ⇒ θ1 = 0°
Como o hexágono é regular, cada um dos arcos P1P2 , P2P3 ,
P3P4 , P4P5 , P5P6 e P6P1 , mede 60°.

2
= – 2
⇒

2
= – 2

⇒

3π
2 < θ < 2π

2
6
2
6
+
i ⇒ |z| = 4 + 4 = 2
2
2

sen θ =

d) z = –2 + 2i 3 ⇒ |z| = 4 + 4 · 3 = 4

1
– 2

6
3
=
2 2
2
– 2
sen θ =
= – 1
2
2 2

cos θ =

c) z = –2 + 2i ⇒ |z| = 4 + 4 = 2 2
cos θ = –

θ = π
4

i) z = –6

3
2
sen θ = 1
2

cos θ =

cos θ = 4

⇒

π
0 < θ < 2

Logo: θ2 = 60°, θ3 = 120°, θ4 = 180°, θ5 = 240° e θ6 = 300°.
θ = 180° + 45°

180° < θ < 270°

Im(z)

θ = 225°

f ) z = 2i

P3

P2

P4

P1

Re(z)

z é imaginário puro e Im(z) > 0 ⇒ θ = 90°
P5


P6

13/05/10 04:33


60. a) z = – 5

3
2

| 10 |

+ 5 i ⇒ ρ =
2

25 · 3 + 25 = 5
4
4

3
– 5 3
= –
cos θ = –
2
2
5
⇒ θ = 150°
5
2
sen θ =
= 1
2
5
Logo: z = 5 (cos 150° + i sen150°).
b) z = – 2 – i 2 ⇒ ρ = 2 + 2 = 2
2
2
2
sen θ = –
2
cos θ = –

⇒ θ = 225°

Logo: z = 2 (cos 225° + i sen225°).
c) z = 2i ⇒ ρ = 2
z é imaginário puro e Im(z) > 0 ⇒ θ = 90°
Logo: z = 2 (cos 90° + i sen 90).
d) z = 1 – i 3 ⇒ ρ = 1 + 3 = 2
cos θ = 1
2

3
sen θ =
2

⇒ θ = 300°

Logo: z = 2 (cos 300° + i sen 300°).
3
⇒ ρ = 1 + 3 = 1
e) z = 1 + i
4
4
2
2
cos θ = 1
2
⇒ θ = 60°
3
sen θ =
2
Logo: z = cos 60° + i sen 60°.

2
cos θ = –5 = –
2
5 2

5
2
=
2
5 2
Logo: z = 5 2 (cos 3π + i sen 3π ).
4
4
sen θ =

i) z = –i ⇒ ρ = 1
z é imaginário puro e Im(z) < 0 ⇒ θ = 3π .
2
3π + i sen 3π .
Logo: z = cos
2
2
3
3
= – 1 – i ⇒ ρ = 1 + 3 = 1
j) z = – 1 , –
16 16 2
4
4
4
4
– 1
4
cos θ = –
= – 1
2
1
2
– 3
3
sen θ = 4 =
2
1
2

k) z = (1 – i)2 = 1 – 2i + i2 = –2i ⇒ ρ = 2
z é imaginário puro e Im(z) < 0 ⇒ θ = 3π
2
3π + i sen 3π ).
Logo: z = 2 (cos
2
2
l) z = 13 ⇒ ρ = 13
z ∈ ℝ e Re(z) > 0 ⇒ θ = 0
Logo: z = 13 (cos 0 + i sen 0).

61. - ρ1 = 3, θ1 = 90° ⇒ z1 = 3 (cos 90° + i sen 90°)

--ρ = 3 + 2 = 5; θ = 180° – 30° = 150° ⇒
2

⇒ z2 = 5 (cos 150° + i sen 150°)

z ∈ ℝ e Re(z) < 0 ⇒ θ = π
Logo: z = 4 (cos π + i sen π).

--ρ = 3 + 2 = 5; θ = 270° + 45° = 315° ⇒
3

3

⇒ z3 = 5 (cos 315° + i sen 315°)

g) z = 3 – 3i ⇒ ρ = 9 + 9 = 3 2
3
2
=
2
3 2
2
sen θ = – 3 = –
2
3 2
cos θ =

⇒ θ = 7π
4

Logo: z = 3 2 (cos 7π + i sen 7π ).
4
4
h) z = (–5, 5) = –5 + 5i ⇒ ρ = 25 + 25 = 5 2


⇒ θ = 4π
3

Logo: z = 1 cos 4π + i sen 4π .
3
3
2

2

f ) z = – 4 ⇒ ρ = 4

⇒ θ = 3π
4

Im(z)
P1
P2
30°
0

3

Re(z)

45°
2

P3

13/05/10 04:33

| 11 |


i
62. - z = 1 + i

-

z
a) =

+ 1
i

(1 – i) i + (– i) = i – i2 – i =
(1 + i)(1 – i) i(– i) 1 – i2 –i2

= i + 1 – 2i = 1 – i
2 2
2

- z = 1 – 2i
2
2

2

2

2
b) .z = 1 – i ⇒ ρ = 1 + 1 =
4
4
2 2
2

Logo: z =

a) x + yi = –1 – 2i (· i)
2xi + y = 1 + i

1
= –i ⇒ x = – i (2)
i
i (–i)

⇒ θ = 315°

- y = –1 + i ⇒ ρ =

- z é imaginário puro e Im(z) < 0 ⇒ θ = 270°.

1
2
= –
2 ⇒ θ = 3π
2
4
1
2
sen θ =
=
2
2

2

Logo: z2 = 1 (cos 270° + i sen 270°).
2
3
– 1 + i
⇒
2
2

3
b) z = 6 cos 4π + i sen 4π = 6 – 1 – i
⇒
2
3
3
4
⇒ z = – 3 – 3i 3
c) z = 3 (cos 90° + i sen 90°) = 3(0 + i) ⇒ z = 3i
d) z = cos 3π + i sen 3π = 0 + i (–1) ⇒ z = – i
2
2
3
e) z = cos 210° + i sen 210° = – + i – 1 ⇒
2
2
3
1 i
⇒ z = –
–
2
2
3
f ) z = 2 (cos 5π + i · sen 5π ) = 2 –
+ i · 1 ⇒
2
6
6
2
⇒ z = – 3 + i
g) z = 2 (cos 135° + i sen 135°) = 2 –


2
2
+ i ·
⇒
2
2

1 + 1 = 2

cos θ = –

z = – 1 · i ⇒ ρ = 1
2
2

63. a) z = 4 (cos 120° + i sen 120°) = 4

3xi = 3 ⇒ –x =

2 (–i) i + y = 1 + i ⇒ y = –1 + i
Assim, temos:
3π
3π
x = –i ⇒ ρ = 1 e θ = ⇒ x = cos + i sen 3π
2
2
2

2

⇒ z = –1 + i

xi – y = –i + 2
2xi + y = 1 + i (1)

⇒ +

2
(cos 315° + i sen 315°).
2

⇒ z = – 2 + 2i 3

⇒

64. x, y ∈ ℂ

= 1 – i + i = – i
4
4 2
2

1
2
2
=
cos θ = –
2
2
2
– 1
2
2
= –
sen θ =
2
2
2

2
2
+ i –
h) z = 3 cos 7π + i · sen 7π = 3
4
4
2
2
2
2
⇒ z = 3 – 3 · i
2
2

Logo: y = 2 (cos 3π + i sen 3π ).
4
4
b) 2x + yi = 0 (· i) ⇒
xi + y = 3 – 3i 3
⇒ + 2xi – y = 0 (1)
xi + y = 3 – 3i 3

3
3xi = 3 – 3i 3 ⇒ x = 1 – i = – 3 – i (2)
i

De (1) : y = 2xi (2) 2i (– 3 – i) ⇒ y = 2 – 2i 3
Assim, temos:

- x = –

3 – i ⇒ ρ = 3 + 1 = 2

3
2
1
sen θ = –
2

cos θ = –

⇒ θ = 210°

Logo: x = 2 (cos 210° + i sen 210°).

- y = 2 – 2i

3 ⇒ ρ = 4 + 12 = 4

2
1
=
4
2
–2 3 = – 3
sen θ = –
4
2

cos θ =

⇒ θ = 300°

13/05/10 04:33


| 12 |

Assim: ρA = ρB = ρC = ρD= 25 + 25 = 5 2 .

Logo: y = 4 (cos 300° + i sen 300°).

65. M: imagem do complexo z = ρ [cos (180° – θ + i ·
· sen (180° – θ)]
Assim: z = ρ (– cos θ + i sen θ) (1)
3
tg θ = 2

9 13
⇒ sec2 θ = 1 + 4 = 4 ⇒ cos2 θ =
2
1 +tg2 θ = sec2 θ
13
4

=
cos θ =
(2)
13 0 < θ < 90°
3
3 2
tg θ = sen θ = 2 ⇒ sen θ = 2 · ⇒ sen θ =
cos θ
13
3 (3)
=
13
Substituindo-se (2) e (3) em (1), obtém-se:

θA = π ⇒ θB = π + π = 3π, θC = π + π = 5π e θc =
4
4
2
4
4
4
π + 3π = 7π
=
4
2
4
Logo: z = 5 2 (cos θ + i sen θ), com θ = π , 3π, 5π ou 7π
4 4 4
4

68. z1 = 6 ( cos 240° + i sen 240°); z2 =
= 2 3 (cos 30° + i sen 30°); z3 = 3(cos 150° + i sen 150°)
a) z1 · z2 = 6 · 2 3 [cos (240° + 30°) + i sen (240° + 30°)] =
= 12 3 (cos 270° + i sen 270°)
b) z3 · z2 = 3 · 2 3 [cos (150° + 30°) + i sen (150° + 30°)] =
= 6 3 (cos 180° + i sen 180°)
c) z1 · z2 · z3 = 6 · 2 3 · 3 · [cos (240° + 30° + 150°) +

2
3
z = ρ – + i
13
13

+ i sen (240° + 30° + 150°)] = 36 3 (cos 420° +

Assim, de modo geral, a forma algébrica de Z é dada por:
z = – 2ρ + 3ρ i
13
13
Logo, se ρ = 13 , obtém-se z = –2 + 3i, uma possível
forma algébrica de z.
Im(z)

+ i sen 420°) = 36 3 (cos 60° + i sen 60°)
z
d) 1 = 6 [cos (240° – 30°) + i sen (240° – 30°)] =
z2
2 3
= 3 (cos 210° + i sen 210°)
z
e) 1 = 6 [cos (240° – 150°) + i sen (240° – 150°)] =
z3
3
= 2 (cos 90° + i sen 90°)
f )

M
θ
O

z2
= 2 3 [cos (30° – 150°) + i sen (30° – 150°)] =
3
z3
= 2 3 [cos (–120°) + i sen (– 120°)] = 2 3 (cos 240° +
3
3

Re(z)

+ i sen 240°)

66. z = i

· i · i · . . . · i = i

21

22

23

29

= i

21 + 22 + ... + 29

(21 + 29)

2

· 9

= i = i
225

5

–5

2
b) v =
cos 11π – 3π + i sen 11π – 3π =
8
8
8
8
2
u

A(5,5)
π
4

C(–5,–5)

2 cos 11π + i sen 11π
8
8

= 2 – 2i

Im(z)

0

8

2
2
= 2 2 cos 7π + i sen 7π = 2 2
– i
=
4
4
2
2

67. afixos: A(5, 5), B(–5, 5), C(–5, –5), D(5, –5)

–5

8

a) u · v = 2 · 2 cos 3π + 11π + i sen 3π + 11π =
8
8
8
8

z = i = cos π + i sen π
2
2

B(–5,5)

69. u = 2 cos 3π + i sen 3π e v =

=
5

D(5,–5)

Re(z)

2
2
2
(cos π + i sen π) =
(–1 + i · 0) = –
2
2
2

c) u2 = u · u = 2 · 2 · cos 3π + 3π + i sen 3π + 3π =
8
8
8
8
2
2
=
= 4 cos 3π + i sen 3π = 4 – – i ·
4
4
2
2
= – 2 2 + 2i 2


13/05/10 04:33

| 13 |


70. a) z1 = 4 (cos 120° + i sen 120°)
z1 · z2 = 2 (cos 270° + i sen 270°) ⇒
⇒ z2 = 2 (cos 270° + i sen 270°)
4 (cos 120° + i sen 120°)
2
Logo: z = 1 [cos (270° – 120°) + i sen (270° – 120°)] ⇒
2
⇒ z2 = 1 (cos 150° + i sen 150°).
2
3
– 3
1
1
– i · ⇒ z2 = – + i
b) z2 = 1
2
4
2
4
2

71. z = 2 (cos 30° + i sen 30°)

a) z3 = 23 (cos 3 · 30° + i sen 3 · 30°) = 8 (cos 90° + i sen 90°) =
= 8 ( 0 + i · 1) = 8i

3
·3
b) z6 = 26 (cos 6 · 0° + i sen 6 0°) = 64 (cos 180° + i sen 180°) =
= 64 (–1 + i · 0) = –64

c) z10 = 210 (cos 10 · 30° + i sen 10 · 30°) = 1 024 (cos 300° +
1 i 3
= 512 – 512 i 3
+ i sen · 300°) = 1024 –
2
2

72. z =

74. z =

π
π
3 1
i ou z = 1 cos – 6 + i sen – 6
–
2
2

π
zn = 1n cos –n 6 + i sen –n π
6

3 + i

a) z = ( 3 + i)4 = ( 3 )4 + 4( 3 )3 i + 6 ( 3 )2 · i2 +
+ 4 ( 3 ) i3 + i4 = 9 + 12i 3 – 18 – 4i 3 + 1 =
= – 8 + 8i 3
b) z = 3 + i = 2 (cos 30° + i sen 30°) ⇒
⇒ z4 = 24 (cos 4 · 30° + i sen 4 · 30°) = 16 (cos 120° +
+ i sen 120°) = 16

3
–1
+ i ·
= – 8 + 8 i 3
2
2

6 – i 2 ⇒ z =2 2 cos 7π + i sen 7π
6
6
z 10 = (– 6 – i 2 ) 10 = (2 2 ) 10 cos 10 · 7π +
6

73. a) z = –

+ i sen 35π =
+ i sen 10 · 7π = 215 cos 35π
6
3
3
3
1
=215 cos 5π + i sen 5π = 215 – i ·
=
2
2
3
3
= 214 – 214 i 3

=

= cos –n π + i sen –n π
6
6
z45 = cos – 15π + i sen – 15π = cos π + i sen π = i
2
2
2
2
z50 = cos – 25π + i sen – 25π =cos – π + i sen – π =
3
3
3
3
= 1 – 3 i
2
2
2

z100 = (z50)2 = 1 – 3 i =
2
2
= 1 –2· 1 · 3 i+
2
4
2

4

2

3 i =
2

= 1 – 3 – 3 i=– 1 – 3 i
2
2
4
4
2

75. a) z0 = i ⇒ z0 = cos π + i sen π

2
2
Seja z = ρ (cos θ + i sen θ), tal que z2 = z0, ou seja,

z2 = ρ2 (cos 2 θ + i sen 2 θ) = cos π + i sen π ⇒
2
2
ρ2 = 1 ⇒ ρ = 1
⇒

2θ = π + k: 2π ⇒ θ = π + kπ, k ∈ ℤ (*)
2
4

Em (*), fazendo-se k = 0, 1, obtém-se:
π
4
5π
2
θ =
4

θ1 =

Logo: i =

2
1
1
b) z = + i ⇒ z = cos π + i sen π
5
5
5
4
4
8

8

2
1
1
+ i = cos 8 · π + i sen 8 · π =
5
5
5
4
4
= 16 (cos 2π + i sen 2π) = 16 (1 + i · 0) = 16
58
58
58
z8 =

c) z = –4 + 4 i 3 ⇒ z = 8 (cos 120° + i sen 120°)
z–6 = (–4 + 4i 3 )–6 = 8–6 (cos (–6) · 120° + i sen (–6) ·


· 120°) = 1 (cos (–720°) + i sen (–720°) = 1 (cos 00 +
218
218
1 (1 + i · 0) = 1
0
+ i sen 0 ) = 18
2
218

2
2
z1 = cos π + i sen π =
+
i
4
4
2
2

2
2
z2 = cos 5π + i sen 5π = – –
i
4
4
2
2
b) z0 = –3 ⇒ z0 = 3 (cos π + i sen π)
z = ρ (cos θ + i sen θ) e z2 = z0 ⇒
⇒ ρ2 (cos 2θ + i sen 2θ) = 3 (cos π + i sen π) ⇒

13/05/10 04:33


| 14 |

ρ2 = 3 ⇒ ρ = 3
⇒
2θ = π + k · 2π, k ∈ ℤ ⇒ θ = π + kπ, k ∈ ℤ
2

Em (*), fazendo-se k = 0, 1 e 2 obtêm-se: θ1 = 2π , θ2 =
9
8π e θ = 14π.
∙
3
9
9
3

Logo: –2 + 2i 3 =

Em (*), fazendo-se k = 0, 1, obtém-se:

θ1 = π
2
3π
θ2 =
2

z1 = 4 cos 2π + i sen 2π
9
9
3

= z = 3 4 cos 8π + i sen 8π
2
9
9
z3 = 4 cos 14π + i sen 14π
9
9
3

Logo: –3 =

z1 = 3 cos π + i sen π =
2
2
= 3 (0 + i · 1) =i 3
z2 = 3 cos 3π + i sen 3π =
2
2
3 [0 + i(–1)] = – i 3

c) zo = – 1 i ⇒ zo = 1 cos 3π + i sen 3π
2
2
4
4

b) z0 = –5 – 5i ⇒ z0 = 5 2 cos 5π + i sen 5π
4
4
⇒ ρ4 (cos 4θ + i sen 4θ) = 5 2 cos 5π + i sen 5π ⇒
4
4
8

ρ4 = 5 2 ⇒ ρ4 = 50 ⇒ ρ = 50
⇒

z = ρ (cos θ + i sen θ) e z2 = zo ⇒
⇒ ρ2 (cos 2θ + i sen 2θ) = 1 cos 3π + i sen 3π ⇒
2
2
4
1 ⇒ ρ = 1
ρ2 =
4
2
⇒
2θ = 3π + k · 2π ⇒ θ = 3π + kπ, k ∈ ℤ (*)
2
4
θ1 = 3π
4 .
Em (*), fazendo-se k = 0,1, obtêm-se:
θ2 = 7π
4

3
3
⇒

3

ρ = 4 ⇒ ρ = 2
3θ = 2π + k · 2π ⇒ θ = 2π + k · 2π , k ∈ ℤ (*)
3
9
3


16
16
8

z2 = 50 cos 13π + i sen 13π
16
16
8

z3 = 50 cos 21π + i sen 21π
16
16
z4 = 50 cos 29π + i sen 29π
16
16
8

c) z0 = 4 3 – 4i ⇒ z0 = 8 cos 11π + i sen 11 π
6
6
6
6

3 ⇒ z0 = 4 cos 2π + i sen 2π
3
3


3

4

Logo: –5 – 5i =

8

2
2
z1 = 1 cos 3π + i sen 3π = 1 · – + i =
2
2
2
2
4
4
2
2
= – + · i
4
4
2
2
z2 = 1 cos 7π + i sen 7π = 1 · – i =
2
2
2
2
4
4
2
2
= – · i
4
4

76. a) z0 = – 2 + 2i

Em (*), fazendo-se k = 0, 1, 2 e 3, obtêm-se: θ1 = 5π ,
16
θ2 = 13π, θ3 = 21π e θ4 = 29π .
16
16
16

=

Logo: – 1 i =
4

4θ = 5π + k · 2π ⇒ θ = 5π + k · π , k ∈ ℤ (*)
4
16
2

5

⇒

ρ5 = 8 ⇒ ρ = 8
5θ = 11π + k · 2π ⇒ θ = 11π + k · 2π , k ∈ ℤ (*)
6
30
5

Em (*), fazendo-se k = 0, 1, 2, 3 e 4, obtêm-se:
θ1 = 11π, θ2 = 23π, θ3 = 7π , θ4 = 47π e θ5 = 59π
30
30
30
30
30
5

Logo: 4 3 – 4i =

13/05/10 04:33

| 15 |


z1 = 8 cos 11π + i sen 11π
30
30
5

z2 = 8 cos 23π + i sen 23π
30
30
5

=

6
6

x = ρ(cos θ + i sen θ) e x3 = x0 ⇒
⇒ ρ3(cos 3θ + i sen 3θ) = 16 cos π + i sen π ⇒
6
6
3

5

z4 = 8 cos 47π + i sen 47π
30
30

⇒

5

z5 = 8 cos 59π + i sen 59π
30
30
5

77. a) x4 + 16 = 0 ⇒ x4 = –16
x0 = –16 ⇒ x0 = 16 (cos π + i sen π)
x = ρ (cos θ + i sen θ) e x4 = x0 ⇒
⇒ ρ4 (cos 4θ + i sen θ) = 16 (cos π + i sen π) ⇒

ρ3 = 16 ⇒ ρ = 2 2
3θ = π + k · 2π ⇒ θ = π + k · 2 π , k ∈ ℤ (*)
6
18
3

Em (*), fazendo-se k = 0, 1 e 2, obtêm-se: θ1 = π ,
18
θ2 = 13π e θ3 = 25π.
18
18
3
Logo: x = 2 2 (cos θ + i sen θ), com θ = π , 13π
18 18
ou 25π.
18

d) x3 = (–1, 3 ) = –1 + i 3
x0 = –1 + i 3 ⇒ x0 = 2 cos 2π + i sen 2π
3
3

ρ4 = 16 ⇒ ρ = 2
⇒

x = ρ(cos θ + i sen θ) e x3 = x0 ⇒ ρ3(cos 3θ + i sen 3θ) =

4θ = π + k · 2π ⇒ θ = π + k · π , com k ∈ ℤ (*)
4
2

= 2 cos 2π + i sen 2π ⇒
3
3

Em (*), fazendo-se k = 0, 1, 2 e 3, obtêm-se: θ1 = π ,
4
θ2 = 3π, θ3 = 5π e θ4 = 7π.
4
4
4
Logo: x = 2(cos θ + i sen θ), com θ = π , 3π , 5π ou
4 4 4
= 7π , ou seja:
4
x = 2 + i 2 , – 2 + i 2 , – 2 – i 2 ou 2 – i 2 .

3

⇒

ρ3 = 2 ⇒ ρ = 2
3θ = 2π + k · 2π ⇒ θ = 2π + k · 2π , k ∈ ℤ (*)
3
9
3

Em (*), fazendo-se k = 0, 1 e 2, obtêm-se: θ1 = 2π , θ2 =
9
= 8π e θ3 = 14π.
9
9
Logo: x = 2 (cos θ + i sen θ), com θ = 2π , 8π ou
9 9
14π.
9
3

b) x4 – 2i = 0 ⇒ x4 = 2i
x0 = 2i ⇒ x0 = 2 cos π + i sen π
2
2
x = ρ (cos θ + i sen θ) e x4 = x0 ⇒
⇒ ρ4 (cos 4θ + i sen 4θ) = 2 cos π + i sen π ⇒
2
2
4

⇒

e) x2 = 1 , – 1 = 1 – 1 i
2
2
2 2
2
x0 = 1 – 1 i = cos 7π + i sen 7π
4
4
2
2 2

ρ4 = 2 ⇒ ρ = 2

x = ρ (cos θ + i sen θ) e x2 = x0 ⇒ ρ2 (cos 2θ + i sen 2θ) =

4θ = π + k · 2π ⇒ θ = π + kπ , k ∈ ℤ (*)
2
8
2

=

Em (*), fazendo-se k = 0, 1, 2 e 3, obtêm-se: θ1 = π ,
8
θ2 = 5π, θ3 = 9π e θ4 = 13π .
8
8
8
4
Logo: x = 2 (cos θ + i sen θ), com θ = π , 5π, 9π
8 8 8
ou 13π .
8
c) x3 – 8 3 – 8i = 0 ⇒ x3 = 8 3 – 8i
x0 = 8 3 + 8i ⇒ x0 = 16 cos π + i sen π
6
6


2
cos 7π + i sen 7π ⇒
2
4
4
4

⇒

2
8
⇒ ρ =
2
2
2θ = 7π + k · 2π ⇒ θ = 7π + kπ, k ∈ ℤ (*)
4
8
ρ2 =

Em (*), fazendo-se k = 0 e 1, obtêm-se: θ1 = 7π e θ2 =
8
= 15π.
8
4

Logo: x =

8
(cos θ + i sen θ), com θ = 7π ou 15π.
2
8
8

13/05/10 04:33


| 16 |

--Os argumentos das raízes quartas formam uma P.A.
360°

78. Dado z = 4i

a) z = 4i ⇒ z = 4 cos π + i sen π
2
2

= 90°.
4
3
Logo: z1 = 2(cos 30° + i sen 30°) = 2
+ i · 1 = 3 + i
2
2
de razão

2
z1 = ρ cos θ + i sen θ e z1 = z ⇒

⇒ ρ (cos 2θ + i sen 2θ) = 4 cos π + i sen π ⇒
2
2
ρ2 = 4 ⇒ ρ = 2
⇒
2θ = π + k · 2π ⇒ θ = π + kπ, k ∈ ℤ (*)
2
4
2

Em (*), fazendo-se k = 0 e 1, obtêm-se: θ1 = π e θ2 =
4
= 5π
4
2 cos π + i sen π
4
4
Logo: z1 = 4i =
π + i sen π
2 cos
4
4
Im(z)

3
z3 = 2(cos 210° + i sen 210°) = 2 – – i · 1 = – 3 – i
2
2
3
= 1 – i 3
z4 = 2(cos 300° + i sen 300°) = 2 1 – i ·
2
2

81. cos 72° + i sen 72° é raiz da equação x5 + k = 0 ⇒
⇒ (cos 72° + i sen 72°)5 + k = 0 ⇒
⇒ (cos 360° + i sen 360°) + k = 0 ⇒
⇒ k = – cos 0° – i · sen 0° ⇒ k = –1
⇒ k = cos 180° + i sen 180°
x = ρ (cos θ + i sen θ) e x3 = k ⇒

P1
2

2

3
= –1 + i 3
z2 = 2(cos 120° + i sen 120°) = 2 –1 + i ·
2
2

⇒ p3 (cos 3θ + i sen 3θ) = cos 180° + i sen 180° ⇒

π
4

0

Re(z)

P2

⇒

ρ3 = 1 ⇒ ρ = 1
3θ = 180° + k · 360° ⇒ θ = 60° + k · 120° , k ∈ ℤ (*)

Em (*), fazendo-se k = 0, 1 e 2, obtêm-se: θ1 = 60°, θ2 =
= 180° e θ3 = 300°.

b) P1 P2 = 2ρ = 2 · 2 = 4

79. zA = 2(cos 60° + i sen 60°) = 2

1 + i · 3 = 1 + i 3
2
2

zB = 2(cos 180° + i sen 180°) = 2(–1 + i · 0) = –2

3
cos 60° + i sen 60° = 1 + i
2
2
3
Logo: k = cos 180° + i sen 180° = –1
3
1
cos 300° + i sen 300° = – i
2
2
Im(z)

3
zc = 2(cos 300° + i sen 300°) = 2 1 – i ·
= 1 – i 3
2
2

1 3
,
2 2

Im(z)
A

0

(–1,0)

1

Re(z)

2
60°
B

1
3
,–
2
2

2 Re(z)

0

82. A = (–1, 0): imagem de z1 = –1 (raiz sexta de z)

C

6

a) z1 = z ⇒ z = z61 = (–1)6 ⇒ z = 1

80. Uma das raízes quartas de –8 + 8i

3 é z1 = 2 (cos 30° +

+ i sen 30°).

--Todas as raízes quartas de –8 + 8i
módulo ⇒ ρ1 = ρ2 = ρ3 = ρ4.


b) z1 = –1 = cos 180° + i sen 180°

--ρ = 1 ⇒ ρ = ρ = ρ = ρ = ρ = 1
--os argumentos principais de z formam uma P.A.
360°
1

2

3

4

5

6

6

3 têm mesmo

de razão

6

= 60°, ou seja:

13/05/10 04:33

| 17 |


θ2 = θ1 – 3 · 60° = 0°
θ3 = θ1 – 2 · 60° = 60°
θ1 = 180° ⇒

θ4 = θ1 – 1 · 60° = 120°

Exercícios complementares
1.

10

a) A = Σ in = (i0 + i1 + i2 + i3) + (i4 + i5 + i6 + i7) +
n=0

θ5 = θ1 + 1 · 60° = 240°

+ i8 + i9 + i10 = i0 + i1 + i2 = 1 + i – 1 = i

θ6 = θ1 + 2 · 60° = 300°

P.A.

Logo: z1 = cos 180° + i sen 180° = – 1

b) A = i · i2 · i3 · ... · i19 · i20 = i1 + 2 + 3 + ... + 19 + 20 = i

z2 = cos 0° + i sen 0° = 1

=i

3
z3 = cos 60° + i sen 60° = 1 + i
2
2

=0

=0

2.

210

(1 + 20) · 20
2

=

= i = –1
2

.
a) n: no natural par ⇒ n = 2p, p ∈ ℕ
p

A = in + i2n + i3n + i4n = i2p + i4p + i6p + i8p = (i2) +

3
z4 = cos 120° + i sen 120° = –1 + i
2
2

p

p

p

2p

+ (i4) + (i2) · (i4) + (i4) = (–1)p + 1p + (–1)p · 12p +

3
z5 = cos 240° + i sen 240° = –1 – i
2
2

+ 12p ⇒

3
z6 = cos 300° + i sen 300° = 1 – i
2
2

⇒ A = 2 · (–1)p + 2 ⇒ A =

2 + 2 = 4, se p é par
–2 + 2 = 0, se p é ímpar

(1) n = 4k

83.

3

1 = ?

--

(3) n = 4k + 2

z0 = 1 ⇒ z0 = cos 0° + i sen 0°

A = in + i–n = in + 1
in

= cos 0° + i sen 0° ⇒

⇒

(1): n = 4k ⇒ in = i4k = (i4)k = 1k = 1 ⇒ A = 1 + 1 = 2
1

ρ3 = 1 ⇒ ρ = 1

(2): n = 4k + 1 ⇒ in = i4k + 1 = i4k · i = i ⇒ A = i + 1 =
i
= i + (–i) = i – i = 0
i(–i)

3θ = 0° + k · 360° ⇒ θ = k · 120°, k ∈ ℤ (*)

Em (*), fazendo-se k = 0, 1 e 2, obtêm-se: θ1 = 0°, θ2 =

(3): n = 4k + 2 ⇒ in = i4k + 2 = i4k · i2 = –1 ⇒ A = –1 +
+ 1 = –2
–1

= 120° e θ3 = 240°.
z1 = cos 0° + i sen 0° = 1
3
z = cos 120° + i sen 120° = –1 + i
Logo: 1 = 2
2
2
1
z3 = cos 240° + i sen 240° = – – i 3
2
2

(4): n = 4k + 3 ⇒ in = i4k + 3 = i4k · i3 = –i ⇒ A = –i + 1 =
–i
i = –i + i = 0
= –i +
(–i)i

3

P P
1 2 3

3
3 ⇒
= 1 (P2P3) · (HP1) = 1 · 2 ·
·
2
2
2
2

3
⇒ AP P P = 3
1 2 3
4

Logo: A = 2, 0 ou –2

3.

ΔAPB equilátero ⇒ h = PH = 2a 3 = a 3
2
a>0

Im(z)

P

b

1 3
P2 – ,
2 2

2a
H

0

, ∀k ∈ ℤ, ou seja,

(4) n = 4k + 3

z = ρ (cos θ + i sen θ) e z3 = z0 ⇒ ρ3 (cos 3θ – i sen 3θ) =

AP

(2) n = 4k + 1

.
b) n: no inteiro ⇒

2a

P1 (1, 0) Re(z)
60°

P3 –

1
3
,–
2
2


A

a

H

a

B

AAPB = 36 3

13/05/10 04:33


| 18 |

1 ⋅ 2a ⋅ a 3 = 36 3
2
a=6
e

7.

z = (3 + i) · (2 – xi) = 6 + x2 + 2 – 3x · i
(2 + xi) · (2 – xi) 4 + x
4 + x2

b=a 3 =6 3
Assim: z = a + bi ⇒ z = 6 + 6i 3

a) Re(z) = 1 ⇒ 6 + x2 = 1 ⇒ x2 – x – 2 = 0 ⇒ x = 2 ou
4+x

Logo: z = (6 + 6i 3 ) = 36 + 36i ⋅ 3 + 72i 3 ⇒
2

z = 3 + i , com x ∈ ℝ
2 + xi

2

2

x = –1

⇒ z2 = –72 + 72i 3

4.

b) Im(z) = 0 ⇒ 2 – 3x = 0 ⇒ 2 – 3x = 0 ⇒ x = 2
4 + x2
3

A = {x ∈ ℤ; |x| < 5} = {x ∈ ℤ; –5 < x < 5} = {–4, –3, –2, ..., 4} ⇒
⇒ n(A) = 9
Seja z ∈ A, z = (a, b).
.
a) a ∈ A e b ∈ A ⇒ (a, b) ∈ (A × A) ⇒ no de pares (a, b)
é n(A × A) = n(A) · n(A) = 9 · 9 = 81

c) Re(z) = Im(z) ⇒ 6 + x2 = 2 – 3x ⇒ 6 + x = 2 – 3x ⇒
4+x
4 + x2
⇒ x = –1

b) (a, b) é imaginário puro ⇒ a= 0 e b ≠ 0 ⇒
.
⇒ (0, b) ∈ {0} × A* no de pares (0, b), com b ≠ 0, é
n({0} × A*) = 1 · n(A*) = 8

8.

2
34x
+ 5x – 45 · i
A = (5 – xi) · (5x + 9i) =
(5x – 9i) · (5x + 9i) 25x2 + 81 25x2 + 81

c) z · z = 20 ⇒ (a + bi) · (a – bi) = 20 ⇒ a2 + b2 = 20 ⇒
⇒ b = ± 20 – a2 ⇒
a, b ∈ A

2
• A ∈ ℝ ⇒ 5x 2 – 45 = 0 ⇒ 5x2 – 45 = 0 ⇒ x = 3

a = –4 ⇒ b = –2 ou b = 2 ⇒ z = –4 – 2i ou z = –4 + 2i

25x + 81

a = –2 ⇒ b = –4 ou b = 4 ⇒ z = –2 – 4i ou z = –2 + 4i

⇒

ou x = –3

a = 2 ⇒ b = –4 ou b = 4 ⇒ z = 2 – 4i ou z = 2 + 4i

• x = 3 ⇒ A =

a = 4 ⇒ b = –2 ou b = 2 ⇒ z = 4 – 2i ou z = 4 + 2i

5.

A = 5 – xi , x ∈ ℝ
5x – 9i

Seja z = a + bi, com a, b ∈ ℝ.
(z)2 + iz = –2 ⇒ (a – bi)2 + i(a + bi) = –2 ⇒ a2 – b2 – 2abi +
+ ai – b = –2 ⇒ a2 – b2 – b + (a – 2ab)i = –2 ⇒
⇒

a2 – b2 – b = –2

x = –3 ⇒ A = 34 · (–3) = – 1
25 · 9 + 81
3

(1)

9.

a – 2ab = 0 ⇒ a (1 – 2b) = 0 ⇒ a = 0 ou b = 1 (2)
2

a)

OB = r = 3; BH = 2
△OHB retângulo

Assim, de (2):

⇒ OH2 + 22 = 32 ⇒ OH = 5

A(–3, 0) ⇒ zA = –3
Logo: B( 5 , 2) ⇒ zB = 5 + 2i
C( 5 , –2) ⇒ zC = 5 – 2i

a = 0 ⇒ b2 + b – 2 = 0 ⇒ b = –2 ou b = 1
(1)

b = 1 ⇒ a2 = –2 + 1 + 1 ⇒ a2 = – 5 ⇒ ∃ a ∈ ℝ
/
2 (1)
4
2
4
Logo: z = i ou z = – 2i.

6.

34 · 3 = 1 ou
25 · 9 + 81
3

b) D =

Seja z = a + bi, com a, b ∈ ℝ, temos:

AABC = 1 · |D| ⇒ AABC = 1 · (12 + 4 5 ) = 6 + 2 5
2
2

u + v + z = (1 + 2i) + (3 + 4i) +(a + bi) =
= (a + 4) + (b + 6)i ∈ ℝ

–3 0 1
5 2 1 = –12 – 4 5
5 –2 1

(1)

Im(z)

u · v · z = (1 + 2i) · (3 + 4i) · (a + bi) =
= (–5 + 10i) · (a + bi) = (–5a – 10b) +
+ (10a – 5b)i ∈ ℝ
De (1): b = –6
De (2): 10a – 5b = 0

B

(2)

2
A

O

Re(z)

⇒a=–3

H
C

Logo: z = –3 – 6i.


13/05/10 04:33

| 19 |


10. Seja z = x + yi, com x, y ∈ ℝ, temos:
z+z=4
z · z = 13

⇒

2x = 4 ⇒ x = 2

Im(z)
4

⇒

x2 + y2 = 13

2

C

⇒ 4 + y2 = 13 ⇒ y = –3 ou y = 3
0

Assim: zA = 2 – 3i ⇒ A = (2, –3); zB = 2 + 3i ⇒ B = (2, 3);

2

Re(z)

*
13. w = 4 + 2i; z = 3a + 4ai, em que a ∈ ℝ+

O = (0, 0)
AABO = 1 · AB · OH = 1 · 6 · 2 = 6
2
2

• h: altura do △ABC ⇒ h = |z| = 9a2 + 16a2 = 25a2 ⇒
⇒ h = 5a

a>0

Im(z)

• b = Re (z · w)

B(2, 3)

3

z · w = (4 + 2i) · (3a + 4ai) ⇒ z = 4a + 22ai ⇒ b = 4a
2
H

0

–3

Re(z)

• AAB = 1 · b · h = 90 cm2 ⇒ 1 · 4a · 5a = 90 ⇒ a = 3 cm
C

2

2

a>0

14. z1 = ρ1(cos θ1 + i sen θ1) e z2 = ρ2 (cos θ2 + i sen θ2), com

A(2, –3)

0 < θ1; θ2 < 90°

11. Seja z = x + yi, com x, y ∈ ℝ, temos:
|z + z| = 6
z · z = 10

⇒

|2x| = 6 ⇒ x = –3 ou x = 3
x2 + y2 = 10

(*)

x = –3 ⇒ y2 = 1 ⇒ y = –1 ou y = 1
x = 3 ⇒ y2 = 1 ⇒ y = –1 ou y = 1
⇒

A(–3, –1); B(–3, 1),
C(3, 1) e D(3, –1)

⇒

• z1 · z2 = 80(cos 16° + i sen 16°)10 ⇒ z1 · z2 = 80 · (cos 160° +
+ i sen 160°) ⇒

(1) ρ1 · ρ2 = 80

(2) θ1 + θ2 = 160° + k1 · 360°
z
z
• 2 = 4(cos 8° + i sen 8°)5 ⇒ 2 = 4(cos 40° + i sen 40°) ⇒
z1
z1
⇒

ρ2
=4
ρ1
(4) θ2 – θ1 = 40° + k2 · 360°
(3)

a) 2p = 2 · BC + 2 · AB = 2 · 6 + 2 · 2 = 16
De (1) e (3) obtêm-se: ρ1 = 2 5 e ρ2 = 8 5 .

b) AABCD = AD · AB = 6 · 2 = 12

De (2) e (4) obtêm-se: (θ1 = 60° e θ2 = 100°) ou

Im(z)
B

1

–3
A

–1

(θ1 = 240° e θ2 = 280°).
C
3 Re(z)
D

Logo: z1 = 2 5 (cos 60° + i sen 60°) e
z2 = 8 5 (cos 100° + i sen 100°)
ou
z1 = 2 5 (cos 240° + i sen 240°) e

12. S = {z ∈ ℂ; |z – (2 + 4i)| = 2}

z2 = 8 5 (cos 280° + i sen 280°)

Se z = x + yi, com x, y ∈ ℝ, temos:
|z – (2 + 4i)| = 2 ⇒ |(x – 2) + (y – 4)i| = 2 ⇒
⇒ (x – 2)2 + (y – 4)2 = 2
(x – 2)2 + (y – 4)2 = 4


15. P: imagem de z1 ⇒ z1 = ρ1(cos 30° + i sen 30°)
Q: imagem de z2 ⇒ z2 = ρ2(cos 120° + i sen 120°)
PQ = 20; ρ1 = 2ρ2
△POQ retângulo

⇒ 4ρ22 + ρ22 = 20 ⇒ ρ2 = 2 ⇒
⇒ ρ1 = 4

13/05/10 04:33


| 20 |

Assim: z1 · z2 = ρ1 · ρ2 (cos (30° + 120°) + i sen (30° + 120°) =

Assim, n = 6.

= 8 · (cos 150° + sen 150°) (f. trigonométrica)

II. –2 3 – 2i = 4 cos 7π + i sen 7π
6
6

e

z2 = (–2 3 – 2i)n ⇒ z2 = 4n cos n · 7π + i sen n · 7π
6
6

3
= i · 1 = –4 3 + 4i
f. algébrica: z1 · z2 = 8 –
2
2

z2 é imaginário puro ⇒ cos n · 7π = 0 ⇒ n · 7π = π +
6
6
2
7n – 3 ∈ ℤ e n ∈ ℤ+
*
+ kπ, k ∈ ℤ ⇒ k =
6

Im(z)
Q

P
ρ2

Como 7n – 3 deve ser múltiplo de 6, então n = 3.

ρ1

b) n = 6 ⇒ z1 = 26(cos 11π + i sen 11π) = 64 (–1 + i · 0) ⇒

30°
O

Re(z)

⇒ z1 = –64
1 + i = 2 (cos 45° + i sen 45°)

n = 3 ⇒ z2 = 43 cos 7π + i sen 7π = 64 (0 + i (–1)) ⇒

2
2

x1 + y1i = (1 + i)9 = ( 2)9 (cos 405° + i sen 405°) =

16. a)

⇒ z2 = –64i

= 16 2 (cos 45° + i sen 45°) = 16 2

2
2
+i·
2
2

19. a)

q e r: quociente e resto da divisão de N por 4
⇒

iN = –1 ⇒ i4q + r = –1 ⇒

x1 + y1 · i = 16 + 16i

N = 4q + r

Logo: P' = (x1, y1) = (16, 16).

⇒ i4q · ir = –1 ⇒ (i2)2q · ir = – 1 ⇒ (–1)2q · ir = –1 ⇒
⇒ ir = –1

b) A distância de P à origem é igual ao módulo de x1 +
+ y1i, ou seja, d = 16 2.

⇒ w = r[cos (2π – θ) + i sen (2π – θ)]

⇒ z1004 = ( 2)1004 · (cos 1255π + i sen 1255π)
z

=z

⇒

⇒ a = b = –1

Assim: z = –1 – i ⇒ z = 2 cos 5π + i sen 5π ⇒
4
4

(cos π + i sen π) = –2

502

⇒

0 ⩽ θ < 2π

⇒ z · w = 1 ⇒ z · w = 1(cos 2π + i sen 2π) ⇒

⇒ (2a – b + 1) + (a – 2b – 1) i = 0 ⇒

502

r=2

w = r(cos θ + i sen θ) ⇒ w = r(cos θ – i sen θ)

i · z + 2 · z + 1 – i = 0 ⇒ i(a + bi) + 2(a – bi) + 1 – i = 0 ⇒

1004

⇒

0⩽r<4

b) z = 2 cos π + i sen π
3
3

17. Seja z = a + bi, com a, b ∈ ℝ, temos:

⇒ 2a – b + 1 = 0
a – 2b – 1 = 0

0⩽r<4

20. a)

2r = 1 ⇒ r = 1
2
π + (2π – θ) = 2π ⇒ θ = π
3
3

80
84
–
z = (1 + i) 96 (1 – i)
i

1 + i = 2 cos π + i sen π ⇒
4
4
⇒ (1 + i)80 = 240(cos 0 + i sen 0) = 240

18. a)

I. 3 – i = 2 cos 11π + i sen 11π
6
6

z1 = ( 3 – i)n ⇒ z1 = 2n cos n · 11π + i sen n · 11π
6
6
z1 ∈ ℝ ⇒ sen n · 11π = 0 ⇒ n · 11π = k · π, k ∈ ℤ ⇒
6
6
*
⇒ k = 11 n ∈ ℤ e n ∈ ℤ+
6


1 –i = 2 cos 7π + i sen 7π ⇒
4
4
⇒ (1 – i)84 = 242 (cos π + i sen π) = –242
i96 = i0 = 1
40
42
Logo: z = 2 + 2 = 240 (1 + 22) = 5 · 240
1
5
b) z = (1 + i 3)
4
(1 – i 3 )

13/05/10 04:33

| 21 |


x15 = 1 ⇒ ρ15(cos 15θ1 + i sen 15θ1) = 1 (cos 0 + i sen 0) ⇒
1

1 + i 3 = 2 cos π + i sen π ⇒ (1 + i 3 )5 =
3
3

⇒

= 25 cos 5π + i sen 5π
3
3

ρ15 = 1 ⇒ ρ1 = 1
1
k1 · 2π
θ1 = 15 , k1 ∈ ℤ

Assim:

1 – i 3 = 2 cos 5π + i sen 5π
3
3

x = cos

(1 – i 3)4 = 24 cos 20π + i sen 20π =
3
3

(2) x = ρ2(cos θ2 + i sen θ2)
x12 = 1 ⇒ ρ12(cos 12θ2 + i sen 12θ2) = 1 (cos 0 + i sen 0) ⇒
1

= 24 cos 2π + i sen 2π
3
3
5
Logo: z = 24 cos 5π – 2π + i sen 5π – 2π
2
3
3
3
3

⇒
=

ρ12 = 1 ⇒ ρ2 = 1
1
k2 · 2π
θ2 = 12 , k2 ∈ ℤ

Assim:

= 2(cos π + i sen π) = –2

x = cos

21. a)

k1 · 2π
k1 · 2π
15 + i sen 15 , com k1 = 0, 1, 2, ..., 14.

k2 · π
k2 · π
6 + i sen 6 , com k2 = 0, 1, 2, ..., 11.

As soluções comuns de (1) e (2) são obtidas nos seguintes

A(0, –2), afixo de z = –2i ⇒ os demais vértices são:

casos:

B(2, 0), C(0, 2) e D(–2, 0)

k1 = k2 = 0 ⇒ θ1 = θ2 = 0
2π
k1 = 5 e k2 = 4 ⇒ θ1 = θ2 = 3
4π
k1 = 10 e k3 = 8 ⇒ θ1 = θ2 = 3

b) AAOB = 1 · 2 · 2 = 2 ⇒ AABCD = 4 · AAOB = 8
2
c) (x – 2i)(x + 2i)(x – 2)(x + 2) = 0 ⇒ (x2 + 4)(x2 – 4) =0 ⇒

Logo, n(S1 ∙ S2) = 3 ⇒ n(S) = 27 – 3 = 24.
(*)

⇒ x4 – 16 = 0

23.

2 C

C
–2

B
2 Re(z)

0

comprimento
do arco (u. c.)

ângulo central
(rad)

4π

Im(z)

2π

π
3

α

π
⇒ α = 6 rad

Assim, temos:
11π
11π
P1: afixo de z1 ⇒ z1 = 2 · cos 6 + i sen 6 = 3 – i ⇒
⇒ z1 = 3 + i
π
π
5
P2: afixo de z2 ⇒ z2 = 2 · cos 2 + i sen 2 = 2 ⇒ z2 = 32

–2 A

22. (x15 – 1) · (x12 – 1) = 0 ⇒ (1) x15 – 1 = 0 ou (2) x12 – 1 = 0
S : conjunto solução de (1)
Sejam S1: conjunto solução de (2)
2

7π
7π
P3: afixo de z3 ⇒ z3 = 2 · cos 6 + i sen 6 = – 3 – i
5
|z1 + z2 + z3| = | 3 + i + 32 – 3 – i| = 32

Im(z)
P2

temos: S = S1 ∙ S2 ⇒ n(S) = n(S1) + n(S2) – n(S1 ∙ S2) =
= 15 + 12 – n(S1 ∙ S2) ⇒
⇒ n(S) = 27 – n(S1 ∙ S2)
soluções comuns

(*)

–2

0
P3

α

2 Re(z)
P1

(1) x = ρ1(cos θ1 + i sen θ1)


13/05/10 04:33

| 22 |


3

3 i
7π
7π
–
= cos 6 + i sen 6
2
2
7π
+ i sen 2 ⇒ w = –i ⇒ w12 = 1

24. w =

–

3

7π
= cos 2 +

• na parte inferior
.
no de pontos:

4

+1

⇒

+2

⇒

5

⇒

3

+4

⇒

7–7

Seja v = ρ(cos θ + i sen θ), tal que v4 = 1, temos:
ρ4 (cos 4θ + i sen 4θ) = 1(cos 0 + i sen 0) ⇒

Logo:

ρ4 = 1 ⇒ ρ = 1
⇒ 4θ = k · 2π ⇒ θ = kπ , k ∈ ℤ (*)
2
Em (*), fazendo-se k = 0, 1, 2 e 3, obtêm-se θ1 = 0,
π
3π
θ2 = 2 , θ3 = π, θ4 = 2 .
v1 = cos 0 + i sen 0 = 1
π
π
v2 = cos 2 + i sen 2 = i
Logo:
v3 = cos π + i sen π = –1
3π
3π
v4 = cos 2 + i sen 2 = –i

25. a)

+3

0

0

+5

⇒

5

+6

⇒ 4

7–7

11 – 7

?
=
?

Testes
1. (a − b)(c − d) = (2 + i − i + 3)(1+ i − 3 + 2i) =
= −2 + 3i) = 10 + 15i
5(
−
Resposta: c.

2. z= x + 2i

ρ2 = ρ4 = ρ5 = ρ7 = 1

z=

θ1 = π ⇒ θ2 = 3 · π = 3π ; θ4 = 7 · π = 7π ; θ5 =
8
8
8
8
8

π = 9π ; θ = 13 · π = 13π
=9·
8
8 7
8
8

x 2 + 22= 2 2 ⇒ x 2 + 4 8
=

⇒ x 2 = ⇒ x = 2 (x é real negativo)
4
−

Logo, z = 2 + 2i ⇒
−

b) r = 2π = π
8
4

⇒ z 2 =−2 + 2i)2 = − 8i − 4 = 8i
(
4
−

π
= π
8
4
1 · 1 · 1 · sen π =
AP OP =
2
4
1
8

c) m(P1OP8) = 2 ·

Resposta: b.

3. a, b, c: números inteiros positivos (*)

2
2
1
=
=2·
2
4
8· 2
=2 2
Aoctógono = 8 · AP OP =
4
1
8

c = (a + bi)2 – 14i ⇒ c = a2 + b2i2 + 2abi – 14i ⇒

⇒ c = a2 – b2 + (2ab – 14)i ⇒
2ab – 14 = 0
(1)
⇒ e
c = a2 – b2, com a2 > b2 (2)

P1
1
O
1

π
8

(2)

De (1): a · b = 7 ⇒ a = 7 e b = 1
(*)

π
8

Logo, de (2): c = 72 – 12 = 48
Resposta: a.
P8

4. (a − 3) + (b + 2)i = 2b + (a − 2)i
a − 3 = 2b ⇒ a = 2b + 3 
 ⇒ 2b + 3 = b + 4 ⇒
b + 2 = a − 2 ⇒ a = b + 4

Desafio
Como em cada metade da peça do dominó a quantidade x de

⇒ b =1⇒ a =5

pontos marcados é tal que 0  x  6, então os padrões estabelecidos obedecem ao sistema de numeração de base 7.
Assim, temos:
• na parte superior
.
no de pontos:
6

+2

⇒

1

–1

⇒

8–7


0

+2

⇒

2

–1

⇒

1

+2

⇒

3

–1

⇒

2

5+
5−
Logo, z = i e z = i
Resposta: a.

5.

z= e z=
a + bi
a − bi
2

z + z − 2z = 3 + 3i

13/05/10 04:33

| 23 |


(

a2 + b2

) + a + bi − 2(a − bi) = 3 + 3i
2

9.

z = a + bi , com a, b ∈ℝ
1+i
|a + bi| =1 ⇒ a2 + b2 = 1 ⇒
• |z| = 1 ⇒ a + bi = 1 ⇒

a2 + b2 + a + bi − 2a + 2bi = 3 + 3i

2
• z = a + bi = (a + bi) (1 – i) = a – ai + bi – bi =
2

1+i
(1 + i) (1 – i)
a + b + (b – a)i
=
2
2
2(b – a)
Re(z) = 2 · Im(z) ⇒ a + b =
⇒
2
2
⇒ a + b = 2b – 2a ⇒ b = 3a (2)

1± 1+ 8 1± 3 a1 = 2
=
⇒a
=
2
2 a2 = −1
Logo, a =2 e b =1⇒ z =2 + i e a =−1e b =1⇒

⇒ z =−1+ i.

{2 + i, −1+ i}

a2 + 9a2 = 2 ⇒ a =

z é tal que: 3z + 2z = 10 + 5i (1)

Logo: a · b =

Seja z = a + bi, com a, b ∈ ℝ, e temos em (1):

5
3 5
⇒ b=
5 (2)
5

Resposta: d.

3(a + bi) + 2(a – bi) = 10 + 5i ⇒ 5a + bi = 10 + 5i ⇒
⇒ 5a = 10 ⇒ a = 2
b=5
Assim: z = 2 + 5i
Logo: z ⋅ z = (2 + 5i)(2 – 5i) = 4 – 25i2 = 29
Resposta: b.

7.

1–i

Substituindo (2) em (1), vem:

Resposta: d.

6.

1+i

⇒ a2 + b2 = 2 ⇒ a + b2 = 2 (1)
2

3b = 3 ⇒ b = 1e a2 + b2 − a = 3 ⇒ a2 − a − 2 = 0 ⇒

S=

|1 + i|

1+i

(a2 + b2 − a) + 3bi =3 + 3i

z = a + bi
w= 6 + 3i
wz =(6 + 3i)(a + bi) =6a + 6bi + 3ai − 3b =
= (6a − 3b) + (3a + 6b)i

10.

5 3 5
3
·
=
5
5
5

917 062 007 4
11

229 265 501

37
10
26
22
20
007
3
917062007

wz = (6a − 3b) − (3a + 6b)i

Logo, i

wz + wz − 5 = 0 ⇒ (6a − 3b) + (3a + 6b)i +
+(6a − 3b) − (3a + 6b)i − 5 = 0 ⇒

= i3 = −i

Resposta: b.

⇒ 2(6a − 3b) − 5 = 0 ⇒ 12a − 6b − 5 = 0 que é

11. Sabe que para n∈ , in + in+1 + in+2 + in+3 =
0

uma equação de reta.
Logo,

Resposta: b.

v = + i2 + i3 +  + i22 =21 + i22 = + i2 = − 1e
i
i
i
i

w = + i2 + i3 +  + i78 =77 + i78 = + i2 = − 1
i
i
i
i

8. z = a + bi e z =

a − bi

iz − 2z + (1+ i) =
0
i(a + bi) − 2(a − bi) + 1+ i =
0
ai − b − 2a + 2bi + 1+ i =
0
( −b − 2a + 1) + (a + 2b + 1)i =
0

=
−b − 2a + 1 0 (×2)

0
2b + a + 1=
0
−2b − 4a + 2 =
(+)

2b + a + 1=
0

− 3a + 3 = 0 ⇒ a = 1⇒ −b − 2 + 1= 0 ⇒ b = −1
Logo, z = 1− i
Resposta: e.

MCA1-Resoluc�o�es-Mercado.indd 148

Assim, v ⋅ w =(i − 1)2 =−1− 2i + 1=−2i
Resposta: d.

a + bi
a − bi
12. z = e z =
z + 5z =12 − 16i
−
a + bi + 5(a − bi) =12 − 16i
−
6a − 4bi =12 − 16i ⇒ 6a =12 ⇒
−
−
⇒ a = 2 e − 4b = 16 ⇒ b =
−
−
4

−
Logo, z = 2 + 4i
z = ( −2)2 + 42 = 20 = 2 5
Resposta: b.

9/2/10 10:48:13 AM


2(1+ i)2 2(1+ 2i − 1)
4i
=
=
=
(1− i)3 (1− i)2 (1− i) (1− 2i − 1)(1− i)

=
13. z
=

| 24 |

z
17. =

−2i(1− i) −2(i + 1)
4i
4i
=
=
=
= −1− i
2
2i − 2i −2(1+ i) (1+ i)(1− i)
2

1+ 3i
(1+ 3i)(1+ 2i)
+ (1− i)6
=
+ [(1− i)2 =
]3
1− 2i
(1− 2i)(1+ 2i)

1+ 2i + 3i − 6
5i − 5
+ (1− 2i −=
1)3
+ ( −2i)3
=
1+ 4
5
=i − 1+ 8i =−1+ 9i

=

Resposta: d.

Logo, z = ( −1)2 + 92 = 82 ≅ 9,06

14. Sejam P1, P2, P3 e P4

as imagens de z, –z, z e –z, respecti-

Resposta: e.

vamente.
Se z = a + bi, em que a, b ∈ ℝ, e temos: P1 = (a, b),
P2 = (–a, –b), P3 = (a, –b) e P4 = (–a, b), com a > b.

18.

• P1P2P3P4 é um retângulo ⇒

2
P1 ∈ λ ⇒ dCP = r2 ⇒ (k – 2)2 + 4 = 13 ⇒ (k – 2)2 = 9 ⇒

⇒ A = (2a) (2b)
2p = 2 · (2a) + 2 · (2b) = 4a + 4b
Im(z)

P4

–a

Assim, a equação de λ é (x – 5)2 + y2 = 13 (1)
Se P = (x, y) é a imagem de z = x + yi, temos:
z – 5 = x – 5 + yi ⇒ |z – 5| = (x – 5)2 + y2 (2)

a Re(z)

P2

Substituindo (1) em (2): |z – 5| = 13

P3

–b

A = 24 ⇒ 4ab = 24 ⇒ ab = 6
2p = 20 ⇒ 4a + 4b = 20 ⇒ a + b = 5

ℝ> 0

1

⇒k = 5

P1(a, b)

b

P1 = (2, 2): imagem de z1 = 2 + 2i
λ: circunferência de raio r = 13 e centro C = (k, 0),
com k > 0

Resposta: b.
⇒ a=3

a>b

19.

z1 = 2 + i ⇒ A = (2, 1)
z2 = –4 + i ⇒ B = (–4, 1)

e b = 2 ⇒ z = 3 + 2i

z3 = bi ⇒ C = (0, b), com b < 0

Resposta: e.

AB = 6 e h = 1 + |b|
AABC = 12 ⇒ 1 · 6 · (1 + |b|) = 12 ⇒ 1 + |b| = 4 ⇒
2
⇒ |b| = 3 ⇒ b = –3

0
15. x 2 − 2ax + a2 + b2 =
2a ± 4a2 − 4(a2 + b2 ) 2a ± −4b2
= =
2
2
z1= a + bi
2a ± 2bi
=
z 2 = a − bi
2

b<0

x=

z1 + z 2 =

Im(z)
1

B

a2 + b2 + a2 + b2 = 2 a2 + b2

–4

0

2

Re(z)

b C

Resposta: c.

Resposta: c.

16. z= x + yi
z + i = x + (y + 1)i

20.

z + 2 = (x + 2) + yi

z + i = z + 2 ⇒ x 2 + (y + 1)2 =

(x + 2)2 + y 2 ⇒

⇒ x + y + 2y + 1= x + 2x + 4 + y ⇒
2

A

2

2

2

 1− i 


 1+ i 

801

 (1− i)(1− i) 
=
 (1+ i)(1− i) 



801

 −2i 
= 

 2 

801

=i)801 =
(−

= i)1 = i
(−
−
Resposta: b.

⇒ 2y − 2x − 3 = 0 ⇒ (x, y) percorrem uma reta.
Resposta: d.


20

20

20

9
21. z = 1 + i27 = 1 + i3 = 1 + i = (1 + i) (1 + i)
1+i
1+i
1+i
(1 – i) (1 + i)

20

=

9/2/10 10:48:14 AM

| 25 |


= 1 + 2i + i
1 – i2

20

=

2i
2

20

.
⇒ π – θ ∈ 1o quadrante.
2
Como π – θ = arg zi, então a imagem de zi pertence
2
.
ao 1o quadrante.

= i20 = i0 = 1

Resposta: a.

22. Os afixos são tais que Re(z) ≥ 0 e

Resposta: a.

z ≤ 1.

Resposta: e.

26.
23. Ao dividirmos 1− i ⋅
quociente z
=

3 por −1+ i, obtemos como

( −1− 3) i ⋅ ( 3 − 1)
+
2
2

Note que o módulo de z vale

⇒ w = r(cos θ – i sen θ) = r[cos(–θ) + i sen(–θ)]
Assim: z · w = 2r cos π – θ + i sen π – θ
6
6
z·w=1⇒

2

2r = 1 ⇒ 2 · |w| = 1 ⇒ |w| = 1
2
r = |w|
⇒ π
θ= π
– θ = k · 2π, k ∈ ℤ ⇒ θ = π – k · 2π ⇒
6
6
6
0 ⩽ θ < 2π

Seu argumento principal θ é tal que

senθ =

( 6 − 2)
(− 2 − 6 )
e cos θ =
4
4

( 6 − 2)
,
4
concluímos que θ pertence ao segundo quadrante;
= 180° − 15° 165°
θ
=

Resposta: c.

Como sen 15° sen(45° −=
=
30°)

Em radianos, θ =

27.

  π
 π 
= cos  3 ⋅  + i sen 3 ⋅ =
z3

 6 
  6
π
π
=
cos + i sen =
i
2
2

11π
12

  π
 π 
= cos  6 ⋅  + i sen 6 ⋅ =
z6

 6
 6 

= cos π + i sen π = −1

Resposta: e

24. z =8 − 4i =4(2 − i)
3π
3π  
2
2

+i
w =  cos + i sen  =  −
2
2
=
4
4   2
2 


= 2 + 2i
−

π
π 
 

= cos  12 ⋅  + i sen 12 ⋅ =
z12

6
6 

 

= cos2π + i sen2π 1
=

z 3 + z 6 + z12 = i − 1+ 1= i

w = 2 − 2 i = 2 (1+ i)
−
−

Resposta: d.

z
4(2 − i)
−2 2 (2 − i)(1− i)
= =
=
w − 2(1+ i)
(1+ i)(1− i)

28. (z – 2)4 = –4 ⇒ z – 2 =

−2 2 (2 − 3i − 1)
=
= (1− 3i)
− 2
1+ 1

4

4

–4 ⇒ z = 2 + –4

4

Calculando –4 , obtêm-se:

Resposta: e.

25. •

z = 3 + i ⇒ z = 2 · cos π + i sen π
6
6
w = r · (cos θ + i sen θ) ⇒

w1 = 2 cos π + i sen π = 1 + i
4
4

z = cos θ – i sen θ ⇒ z = cos (–θ) + i sen (–θ)
i = cos π + i sen π
2
2
Assim: z · i = cos π – θ + i sen π – θ .
2
2

⇒
• 0 < θ < π x(–1) – π < –θ < 0 ⇒ 0 < π – θ < π ⇒
π
2
2
2
2

w2 = 2 cos 3π + i sen 3π = –1 + i
4
4
w3 = 2 cos 5π + i sen 5π = –1 – i
4
4
w4 = 2 cos 7π + i sen 7π = 1 – i
4
4

2


9/2/10 10:48:16 AM


| 26 |

4

Como z = 2 + –4 , então z m = 2 + w m, em que
m = 1, 2, 3 e 4.
Assim, obtemos: z1 = 3 + i, z2 = 1 + i, z3 = 1 – i e z4 =
= 3 – i, cujas respectivas imagens são: P1(3, 1), P2(1, 1), P3(1, –1)
e P4(3, –1).
Logo: P1P2P3P4 é um retângulo cuja área é A = 2 · 2 = 4.
Im(z)
P2

1

0
–1

3 Re(z)

P3

360º
x

⇒x=

5
· 360º = 30º
60

Ao girar 30º no sentido horário, P1 passa a ser imagem do
complexo z, no qual ρ = 2 e θ = arg z = 150º – 30º = 120º.
Logo: z = 2(cos 120º + i sen 120º) ⇒ z = –1 + i 3.
Resposta: c.

P1

1

giro de P1
60 min
5 min

1 – cotg
31. z = 1 + i 1 x = (1 + i cotg ix) (1 –x cotg x) =
i
cotg
=

P4

1 – i cotg x
1 – i cotg x
cotg x
1
=
=
–
·i=
1 + cotg2 x
cossec2 x
cossec2 x cossec2 x

= sen2 x – i · (sen x) · (cos x)

Resposta: e.

Logo: |z| = sen4 x + (sen2 x) (cos2 x) =
= sen2 x (sen2 x + cos2 x) = sen2 x = |sen x|

29. ρA = 2 e θA = 60º

=1

A é imagem de zA = 2(cos 60º + i sen 60º)

Resposta: e.

B, C e D: demais vértices do quadrado ⇒
θB = 60º + 90º = 150º
θC = 150º + 90º = 240º ⇒
θD = 240º + 90º = 330º

⇒ ρB = ρC = ρD = 2 e

zB = 2(cos 150º + i sen 150º) ⇒ zB = – 3 + i
⇒ z = 2(cos 240º + i sen 240º) ⇒ z = –1 –i 3
C
C
zD = 2(cos 330º + i sen 330º) ⇒ zD = 3 – i
Resposta: e.

30.

z1 = – 3 + i ⇒ ρ1 = 2 e θ1 = 150º
P1: extremidade do ponteiro dos minutos (imagem de z1)
Im(z)

P1
2

150°
0

2

Re(z)

Como, a cada hora, P1 dá uma volta completa sobre a
circunferência, temos:


9/2/10 10:48:13 AM

Mca3 resol.cap5

Mais conteúdo relacionado

Mais procurados

Semelhante a Mca3 resol.cap5

Último

Mca3 resol.cap5