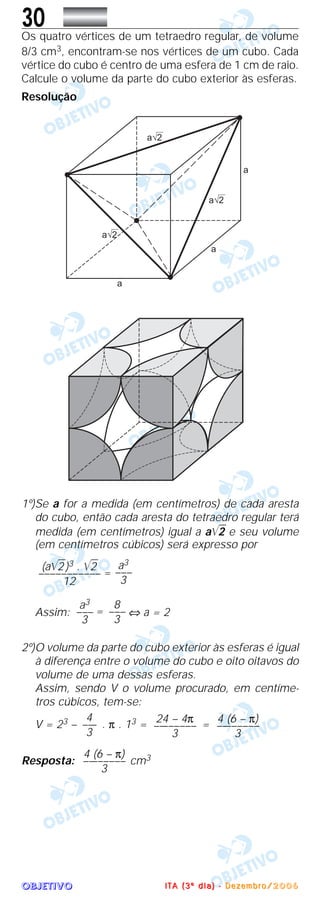
O documento apresenta três problemas matemáticos relacionados a conjuntos, progressões aritméticas e equações. O primeiro problema trata de conjuntos e progressões aritméticas, o segundo de subconjuntos e o terceiro de equações complexas e soma de quadrados.













![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
17 AAAA
Sejam A:(a, 0), B:(0, a) e C:(a, a), pontos do plano car-
tesiano, em que a é um número real não nulo. Nas alter-
nativas abaixo, assinale a equação do lugar geométrico
dos pontos P:(x, y) cuja distância à reta que passa por A
e B, é igual à distância de P ao ponto C.
a) x2 + y2 – 2xy – 2ax – 2ay + 3a2 = 0
b) x2 + y2 + 2xy + 2ax + 2ay + 3a2 = 0
c) x2 + y2 – 2xy + 2ax + 2ay + 3a2 = 0
d) x2 + y2 – 2xy – 2ax – 2ay – 3a2 = 0
e) x2 + y2 + 2xy – 2ax – 2ay – 3a2 = 0
Resolução
Sendo A(a;0), B(0;a), C(a;a) e P(x;y), temos:
1º) reta AB: + = 1 ⇔ x + y – a = 0
2º) distância de P à reta AB:
dP,AB =
3º) distância entre os pontos P e C:
dP,C = (x – a)2 + (y – a)2
4º) dP,AB = dP,C ⇒ =
= (x – a)2 + (y – a)2 ⇔
⇔ (x + y – a)2 = 2 . [(x – a)2 + (y – a)2] ⇔
⇔ x2 + y2 – 2xy – 2ax – 2ay + 3a2 = 0
͉x + y – a͉
––––––––––––
͙ළළ2
͉x + y – a͉
––––––––––––
͙ළළ2
y
–––
a
x
–––
a
IIII TTTT AAAA (((( 3333 ºººº dddd iiii aaaa )))) ---- DDDD eeee zzzz eeee mmmm bbbb rrrr oooo //// 2222 0000 0000 6666](https://image.slidesharecdn.com/ita20073dia-130425173309-phpapp02/85/Ita2007-3dia-14-320.jpg)
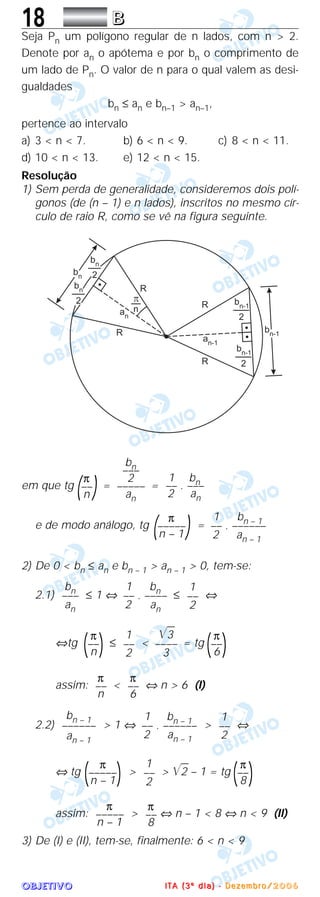


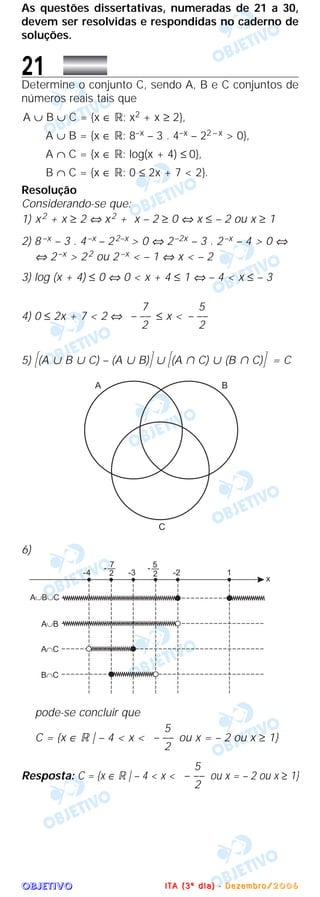


![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
25Sendo x, y, z e w números reais, encontre o conjunto
solução do sistema
log [(x + 2y)(w – 3z)–1] = 0,
2x+3z – 8 . 2y–3z+w = 0,
3
͙ළළළළළළළළළළළළළළළළළළළළළළ2x + y + 6z – 2w – 2 = 0.
Resolução
1) log [(x + 2y) (w – 3z)–1)] = 0 ⇔
⇔ = 1 ⇔ x + 2y = w – 3z ⇔
⇔ x + 2y + 3z = w (I)
2) 2x + 3z – 8 . 2y – 3z + w = 0 ⇔
⇔ 2x + 3z = 23 + y – 3z + w ⇔
⇔ x + 3z = 3 + y – 3z + w ⇔
⇔ x – y + 6z = 3 + w (II)
͙ළළළළළළළළළළළළළළළළළළළළ3)
3
2x + y + 6z – 2w – 2 = 0 ⇔
⇔ 2x + y + 6z – 2w = 8 ⇔
⇔ 2x + y + 6z = 2w + 8 (III)
De (I), (II) e (III), fazendo w = k, temos:
Resposta: (x, y, z, w) = + k, – , – , k ,∀k ≠ – 5
5
––
3
8
––
3
31
–––
3
31 8 5
x = ––– + k y = – –– z = – –– w = k, ∀k ≠ – 5
3 3 3
31 + 3k
x + 2y + 3z = k x = ––––––––
3
8⇔
Ά – x – 5y = 3 – k ⇔
Άy = – –––
3
8 5
y = – –– z = – –––
3 3
x + 2y + 3z = k x + 2y + 3z = k
Άx – y + 6z = 3 + k ⇔
Ά – x – 5y = 3 – k ⇔
2x + y + 6z = 2k + 8 – 3y = 8
(x + 2y)
–––––––
w – 3z
IIII TTTT AAAA (((( 3333 ºººº dddd iiii aaaa )))) ---- DDDD eeee zzzz eeee mmmm bbbb rrrr oooo //// 2222 0000 0000 6666](https://image.slidesharecdn.com/ita20073dia-130425173309-phpapp02/85/Ita2007-3dia-21-320.jpg)