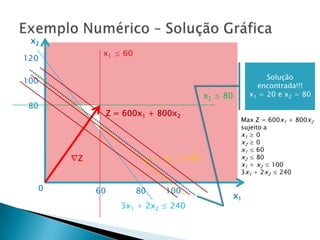
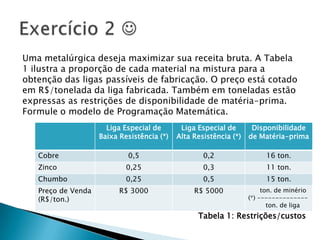
O documento apresenta um exemplo numérico de programação linear para maximizar o lucro de um agricultor cultivando dois tipos de cereais, sujeito a restrições de área, mão-de-obra e demanda do mercado. É formulado o modelo matemático para maximizar a função objetivo Z = Lucros, sujeito às restrições de área, mão-de-obra, produção e demanda. A solução é encontrada graficamente.

1. Matemática ComputacionalProgramação LinearAula 002

2. Programação LinearAula 002Exercícios e Solução GráficaFlávio Augusto de Freitas

3. O problema da tomada de decisão leva em conta variáveis e as condições que “prendem” estas variáveis, às quais denominaremos restrições.Há problemas que envolvem milhares de restrições e variáveis.Geralmente, uma decisão está ligada a certo objeto: minimizar os custos de produção, maximizar os lucros, melhorar as condições de vida de uma população etc.Discussão Geral

4. Um agricultor deseja cultivar duas variedades de cereais, digamos A e B, em uma área restrita a um hectare, sendo que cada are cultivado pelo cereal A produz 8 sacas, enquanto cada are cultivado pelo cereal B produz 10 sacas. Para o plantio, cada are cultivado de cereal tipo A precisa de 3 homens-hora (Hh), sendo que se dispõe de até 240 Hh de trabalho para o cultivo. O custo da mão-de-obra é de 200 R$/Hh. A demanda máxima é limitada pelo mercado consumidor a 480 sacas de cereal tipo A, vendido a 150 R$/saca, e 800 sacas de cereal tipo B, vendido a 120 R$/saca. O agricultor deseja planejar sua produção de forma a maximizar o lucro.Exemplo Numérico

5. Sejam x1 = quantidade de ares cultivados pelo cereal tipo A, e x2 = quantidade de ares cultivados pelo cereal tipo B.Passemos agora à formulação da função objetivo: maximizar o lucro.Lucro = Receitas – CustosReceita cereal A é igual a8 sacas/are x x1 ares x 150 R$/saca = R$ 1200x1Receita cereal B é igual a10 sacas/are x x2 ares x 120 R$/saca = R$ 1200x2Receitas = 1200x1 + 1200x2Exemplo Numérico - Modelagem

6. Os únicos custos considerados nesse modelo são os de pagamento de mão-de-obra.A mão-de-obra de cultivo do cereal A será 3 Hh/are x x1 ares = 3x1Hh.Esse trabalho é remunerado a 200 R$/Hh = R$ 600x1, para o cereal A.Para o cereal B, 2x2Hh x 200 R$/Hh = R$ 400x2. Assim,Custos = 600x1 + 400x2Exemplo Numérico - Modelagem

7. Tomando-se agora o lucro Z = Receitas – Custos, tem-se Z = 1200x1 + 1200x2 - (600x1 + 400x2), ou Z = 600x1 + 800x2.Agora serão formadas as restrições.Um hectare de terra disponível para o cultivo corresponde a 100 ares. Assim, a área cultivada pelo cereal tipo A mais a área cultivada pelo cereal tipo B devem ocupar parte ou toda essa área de 100 ares, o que se traduz por meio da restrição x1 + x2 ≤ 100.Exemplo Numérico - Modelagem

8. Já o consumo de homens-hora mede-se por 3x1 para o cultivo do cereal tipo A, pois cada are cultivado por cereal A precisa de 3 homens-hora.O cultivo de cereal tipo B necessita ao todo de 2x2 homens-hora.O consumo total será a soma dessas quantias e não poderá exceder a 240. Assim, 3x1 + 2x2 ≤ 240.Exemplo Numérico - Modelagem

9. A quantidade total de sacas do cereal tipo A é de 8x1, pois cada are produz 8 sacas.Essa quantidade produzida será não superior à demanda máxima do mercado consumidor, e assim 8x1 ≤ 480, ou, o que é o mesmo, x1 ≤ 60.Para a demanda máxima do cereal tipo B, teremos 10x2 ≤ 800, ou x2 ≤ 80.Além do mais, essas quantidades não podem assumir valores negativos, pois não há nenhum sentido nisso.Exemplo Numérico - Modelagem

10. O modelo matemático completo para esse problema traduz-se por:Max Z = 600x1 + 800x2sujeito a x1 + x2 ≤ 1003x1 + 2x2 ≤ 240 x1 ≤ 60 x2 ≤ 80 x1 ≥ 0 x2 ≥ 0Exemplo Numérico - Modelagem

11. Exemplo Numérico – Solução Gráficax2x1 ≤ 60120Solução encontrada!!!x1 = 20 e x2 = 80100x2 ≤ 8080Z = 600x1 + 800x2Max Z = 600x1 + 800x2sujeito ax1 ≥ 0x2 ≥ 0x1 ≤ 60x2 ≤ 80x1 + x2 ≤ 1003x1 + 2x2 ≤ 240x1 + x2 ≤ 100∇Z06010080x13x1 + 2x2 ≤ 240

12. Uma empresa pode fabricar, com uma máquina trabalhando 45 horas por semana, três artigos diferentes: P1, P2 e P3.O artigo P1 dá um lucro líquido de R$ 4, o artigo P2 de R$ 12 e o artigo P3 de R$ 3.Os rendimentos da máquina são, respectivamente, para os três produtos, 50, 25 e 75 artigos por hora.Um estudo de mercado mostrou que as possibilidades de venda não ultrapassam 100 objetos P1, 500 objetos P2 e 1500 objetos P3, por semana.Pede-se que se reparta a capacidade de produção entre os três produtos, de maneira que se maximize o lucro líquido total.Exercício 1 

13. Uma empresa pode fabricar, com uma máquina trabalhando 45 horas por semana, três artigos diferentes: P1, P2 e P3.O artigo P1 dá um lucro líquido de R$ 4, o artigo P2 de R$ 12 e o artigo P3 de R$ 3.Os rendimentos da máquina são, respectivamente, para os três produtos, 50, 25 e 75 artigos por hora.Um estudo de mercado mostrou que as possibilidades de venda não ultrapassam 100 objetos P1, 500 objetos P2 e 1500 objetos P3, por semana.Pede-se que se reparta a capacidade de produção entre os três produtos, de maneira que se maximize o lucro líquido total.Exercício 1  - Modelagemx1, x2, x3 = horas de máquinax1 + x2 + x3 ≤ 4550x1 ≤ 100 ⇒ x1 ≤ 225x2 ≤ 500 ⇒ x2 ≤ 2075x3 ≤ 1500 ⇒ x3 ≤ 20Z = 50x1.4 + 25x2.12 + 75x3.3Z = 200x1 + 300x2 + 225x3Max Z = 200x1 + 300x2 + 225x3Sujeito ax1 + x2 + x3 ≤ 45x1 ≤ 2x2 ≤ 20x3 ≤ 20x1 ≥ 0x2 ≥ 0x3 ≥ 0

14. Uma metalúrgica deseja maximizar sua receita bruta. A Tabela 1 ilustra a proporção de cada material na mistura para a obtenção das ligas passíveis de fabricação. O preço está cotado em R$/tonelada da liga fabricada. Também em toneladas estão expressas as restrições de disponibilidade de matéria-prima. Formule o modelo de Programação Matemática.Exercício 2 Tabela 1: Restrições/custos

15. ?

16. Flávio Augusto de Freitashttp://sites.google.com/site/flavioifetrpflaviocefetrp@gmail.com

17. FIM