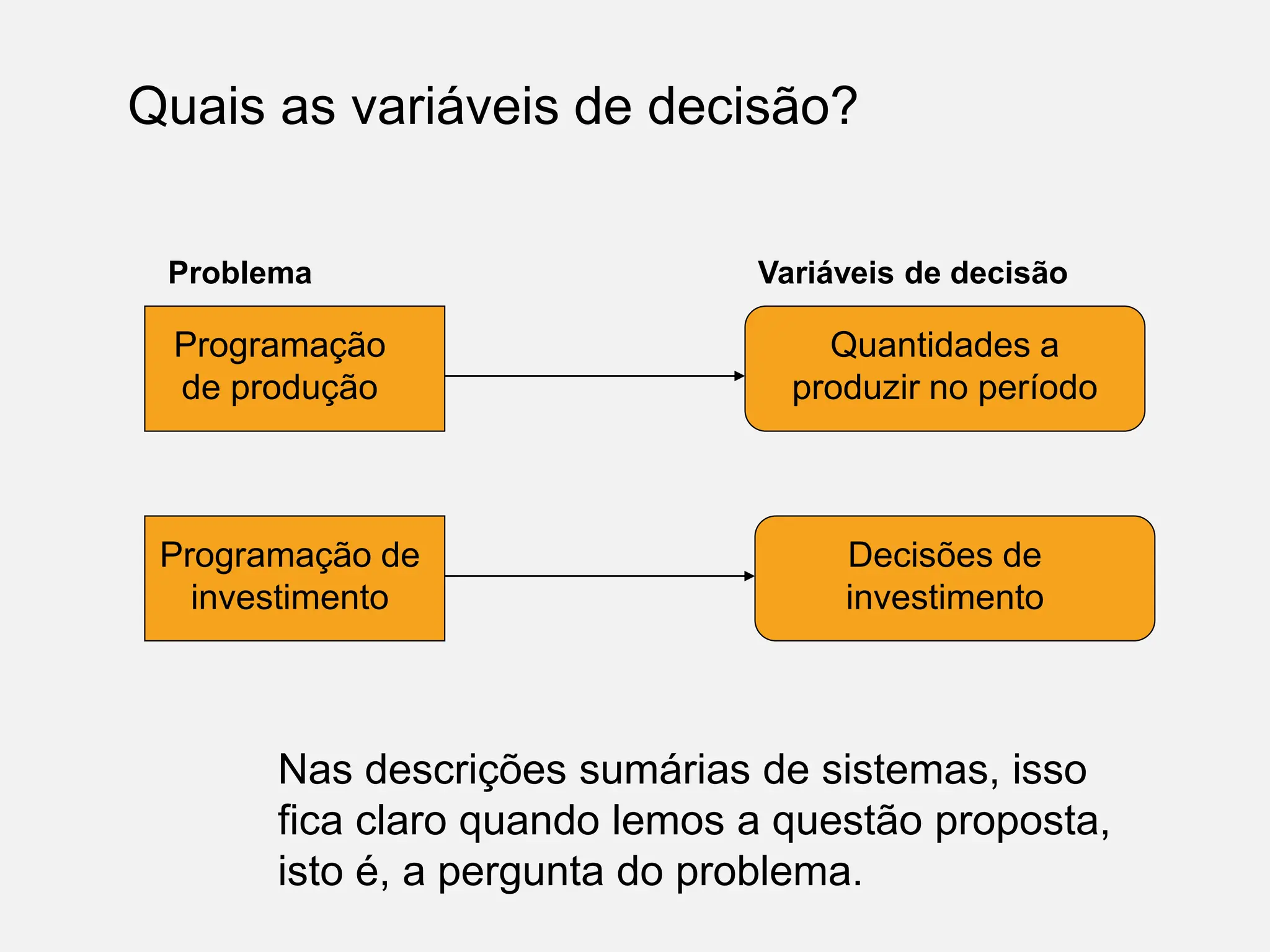
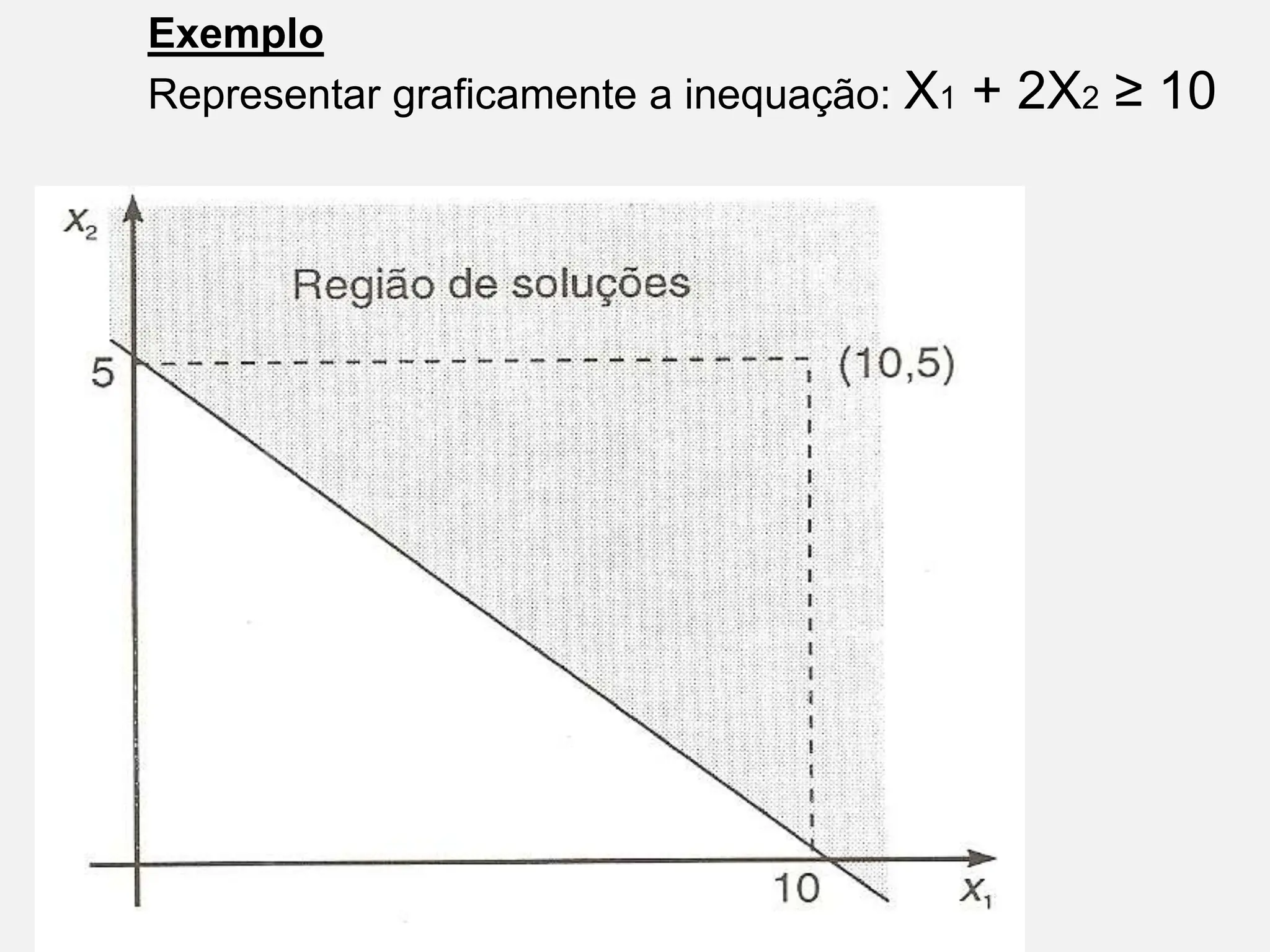
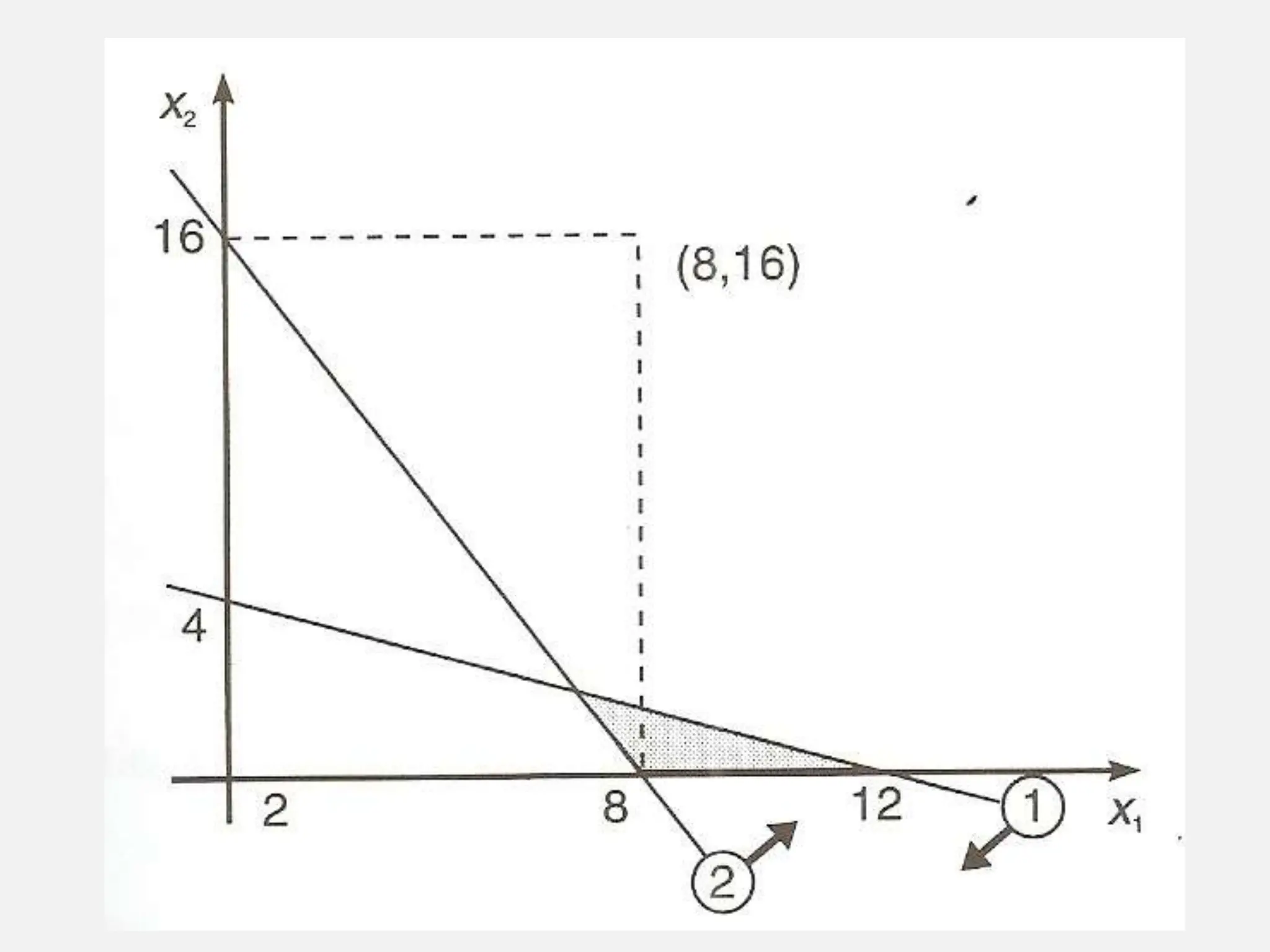
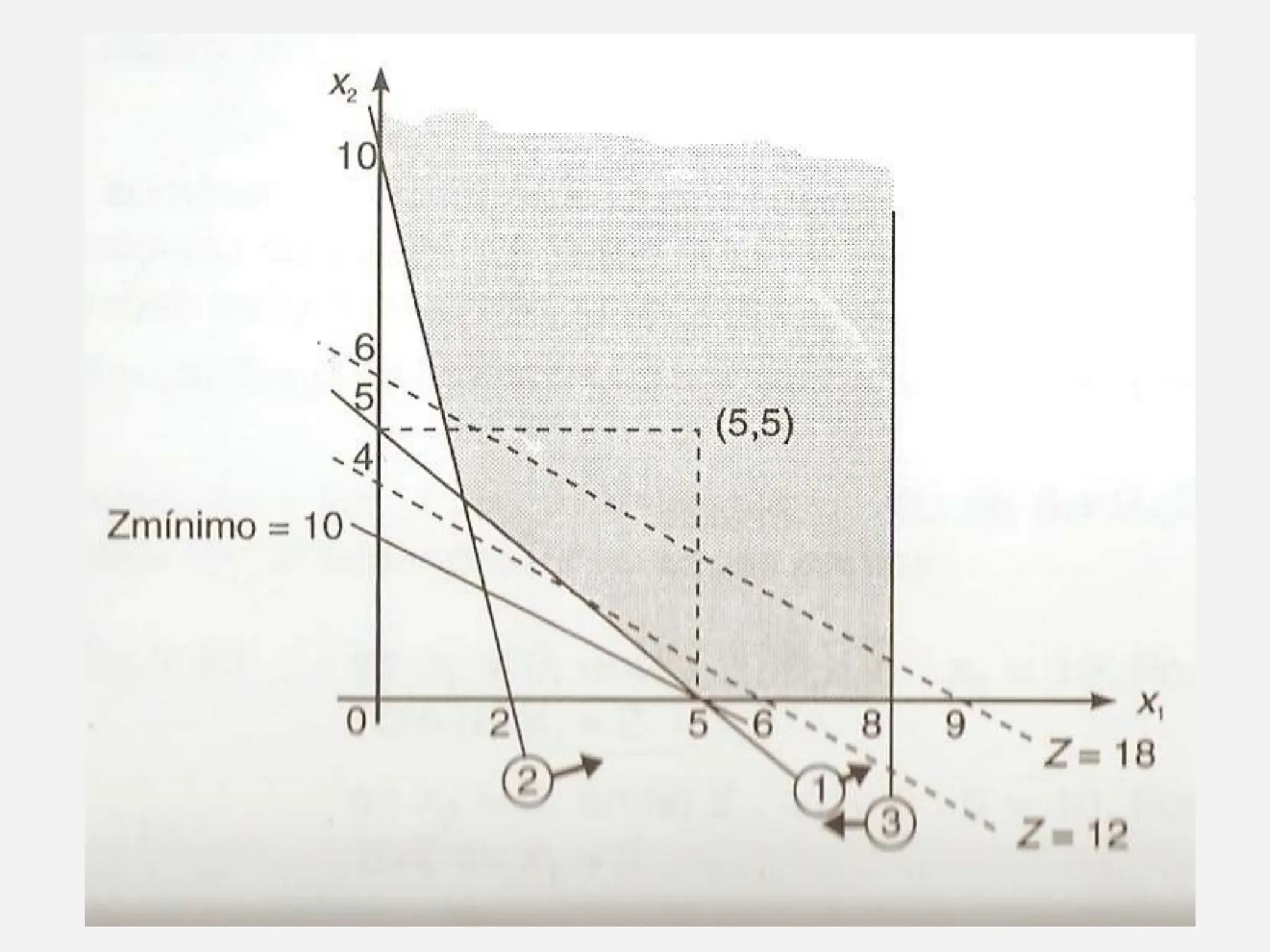
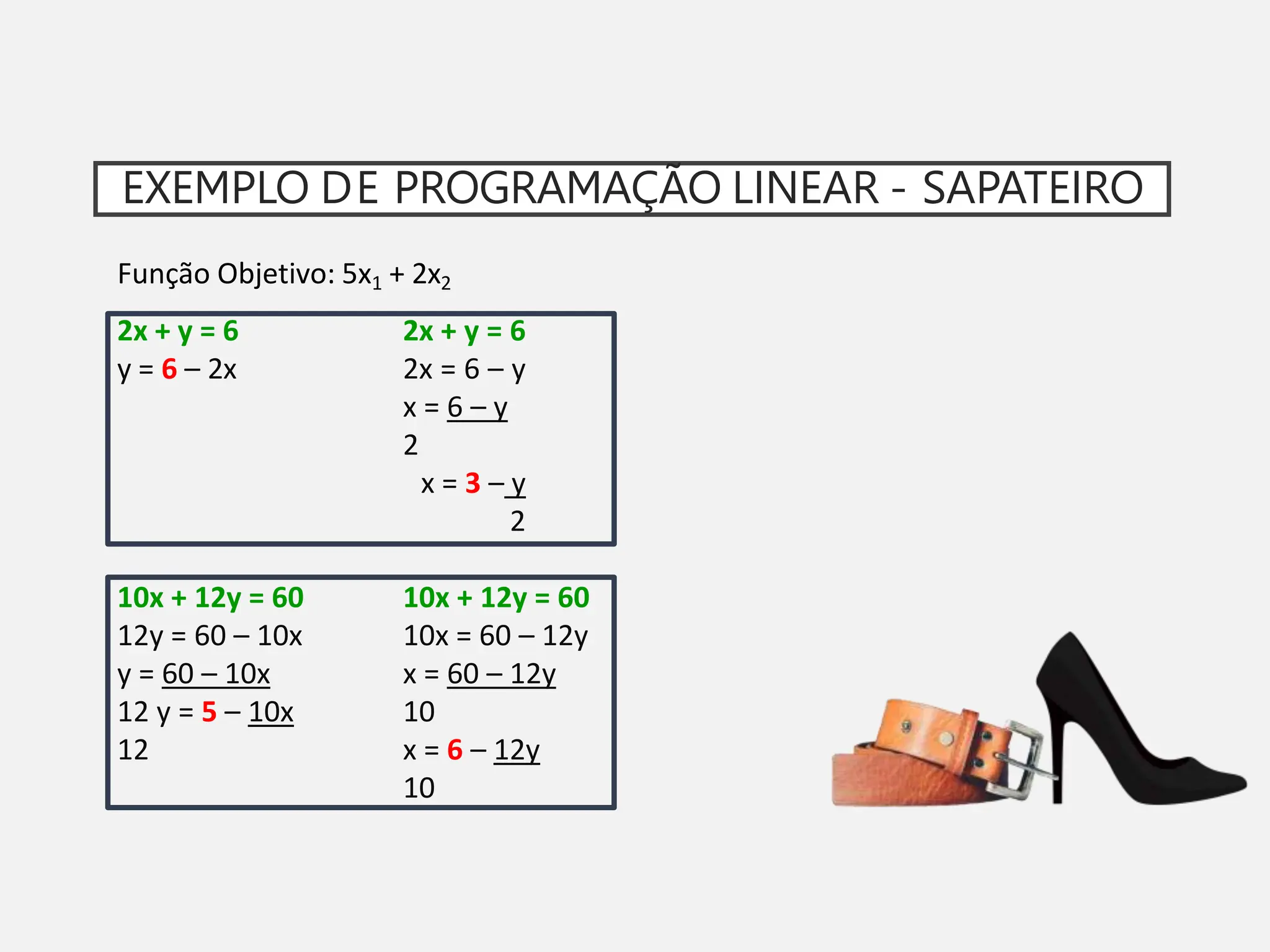
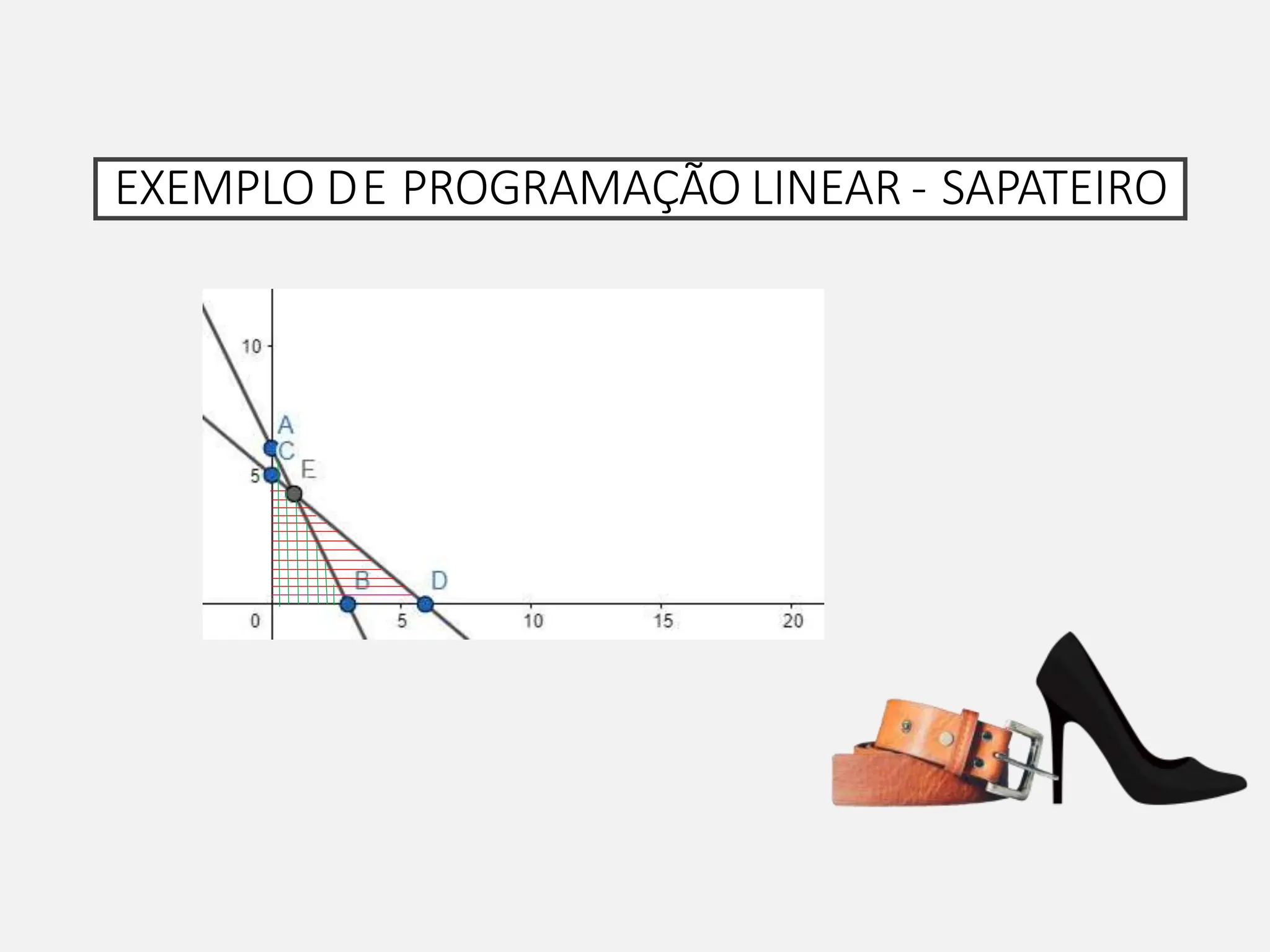
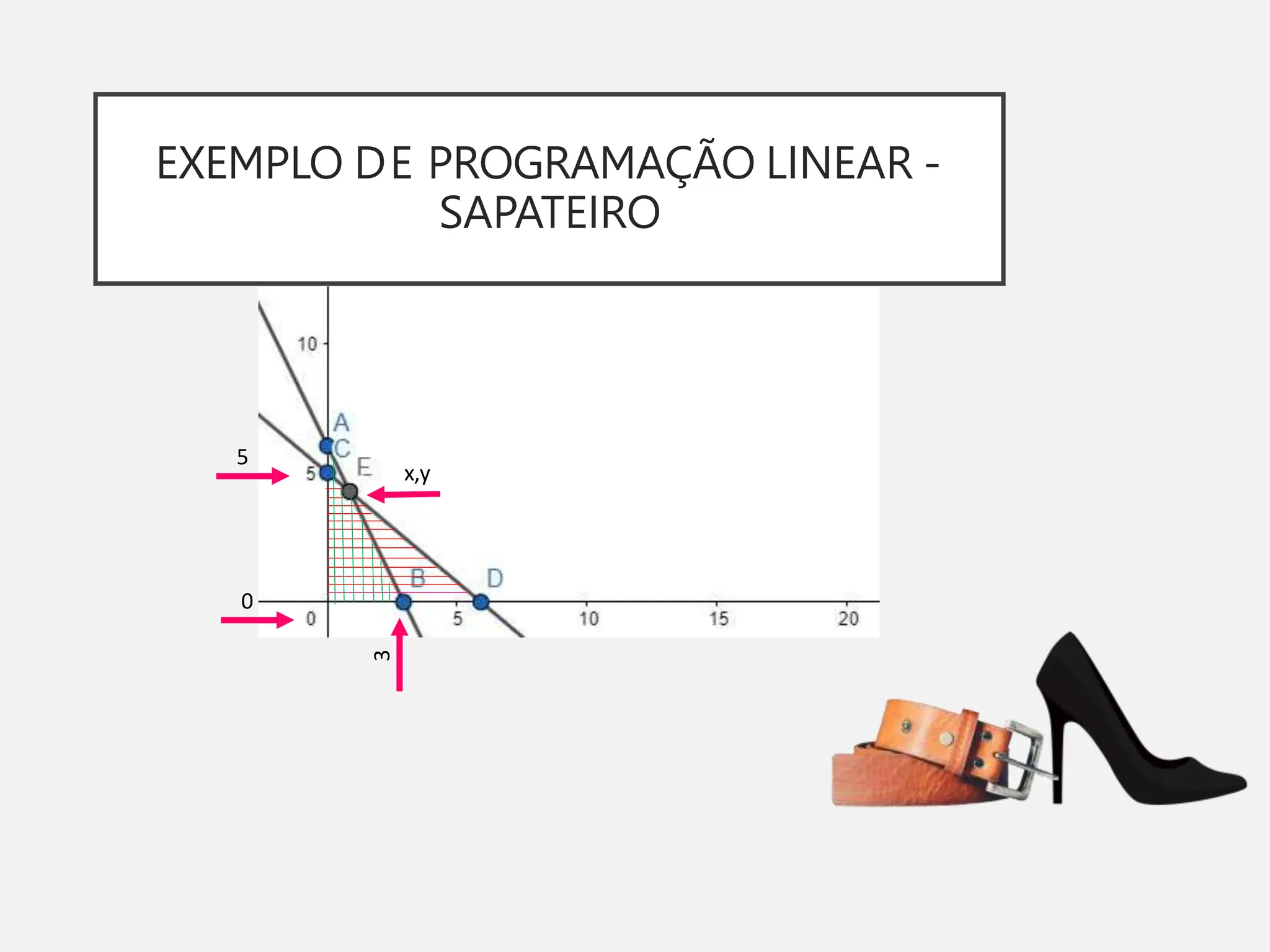
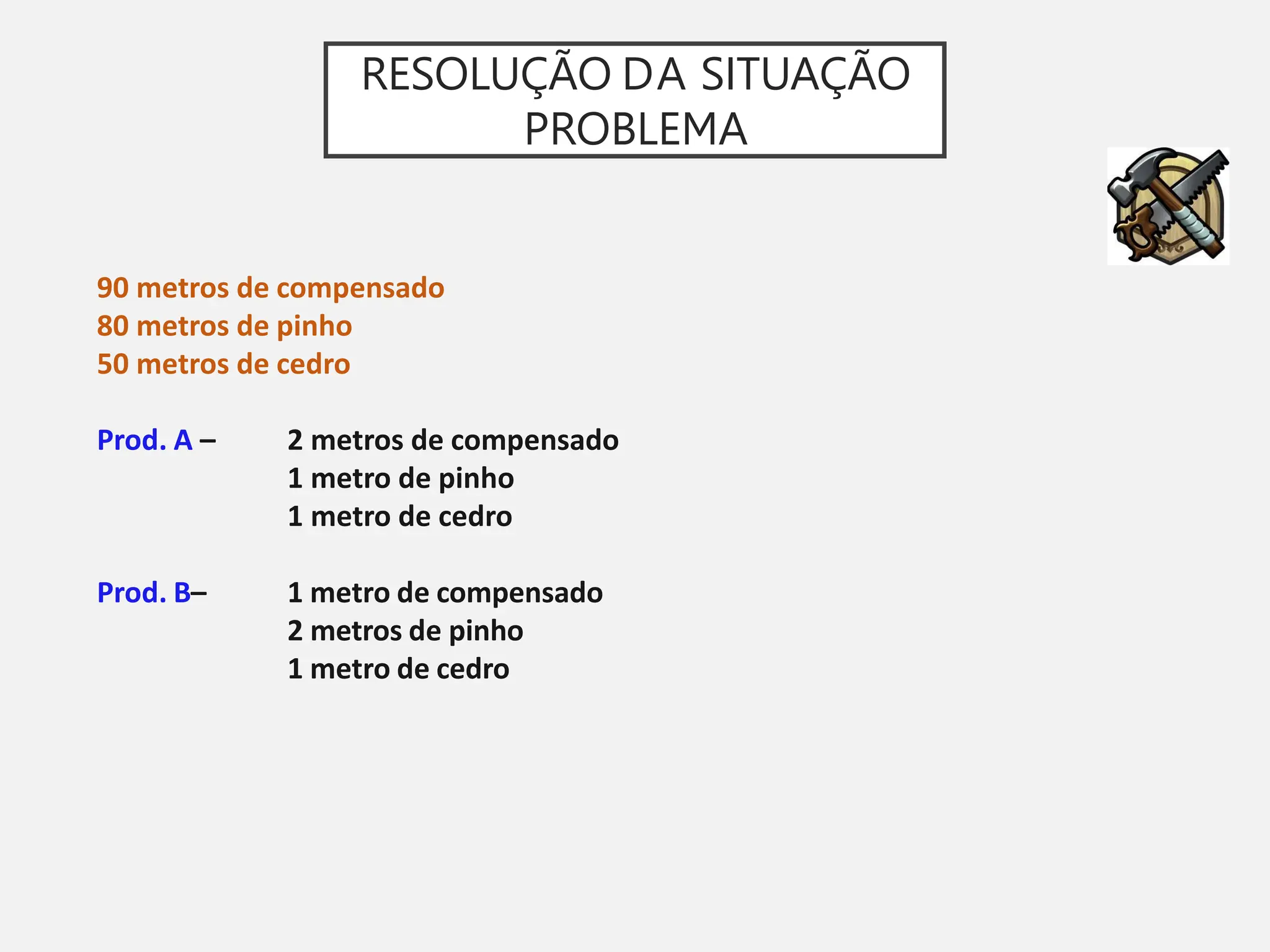
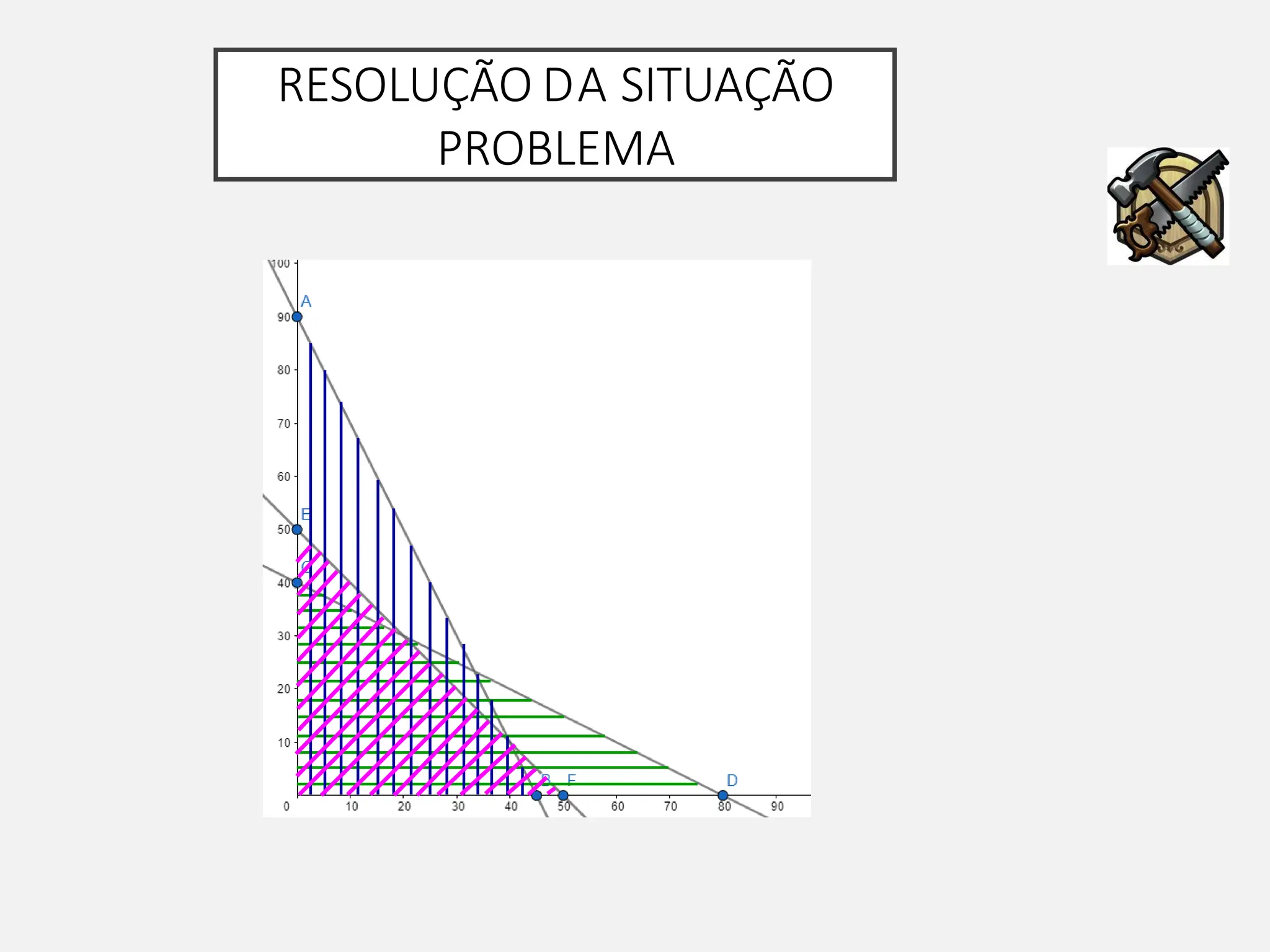
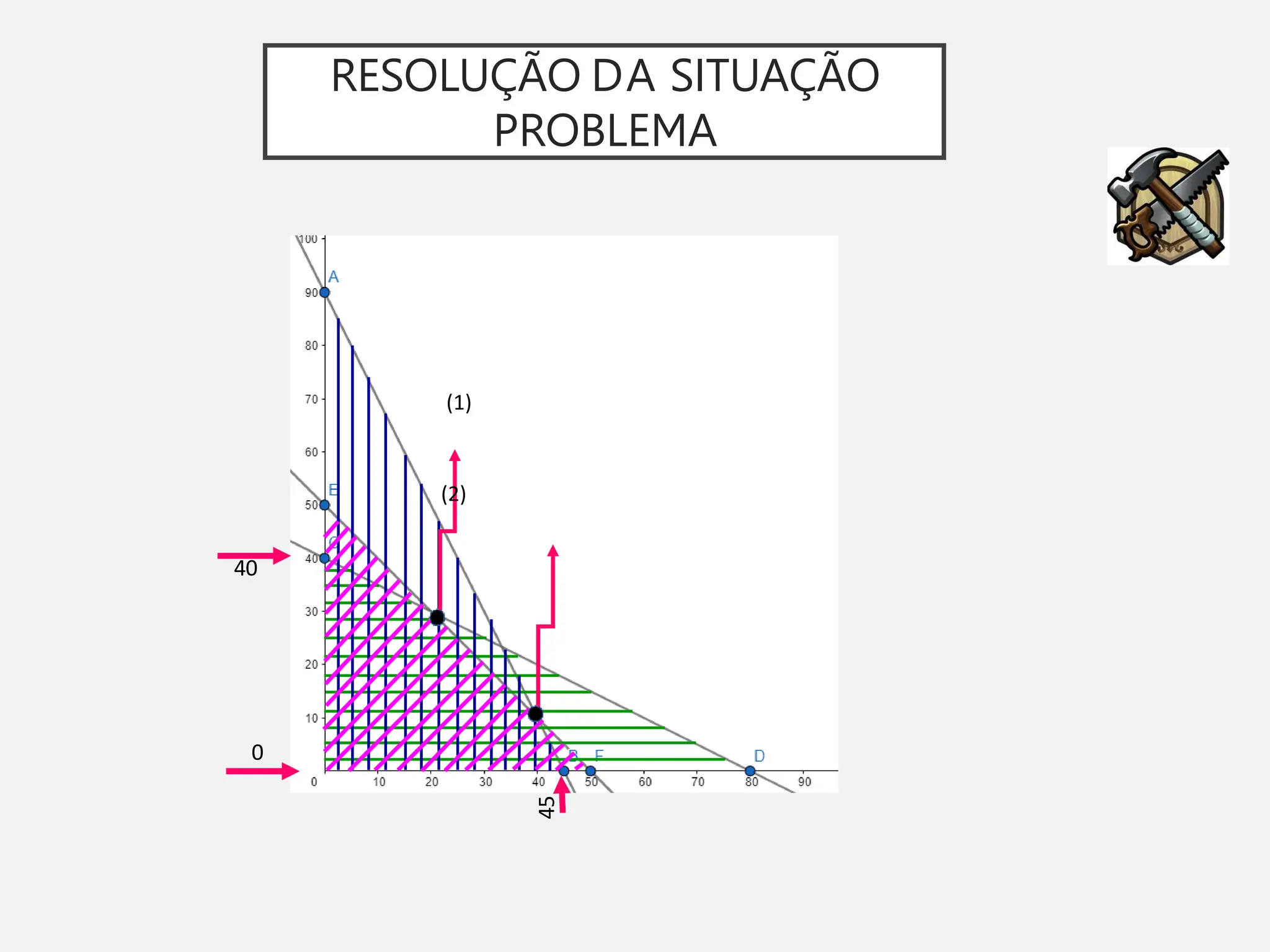
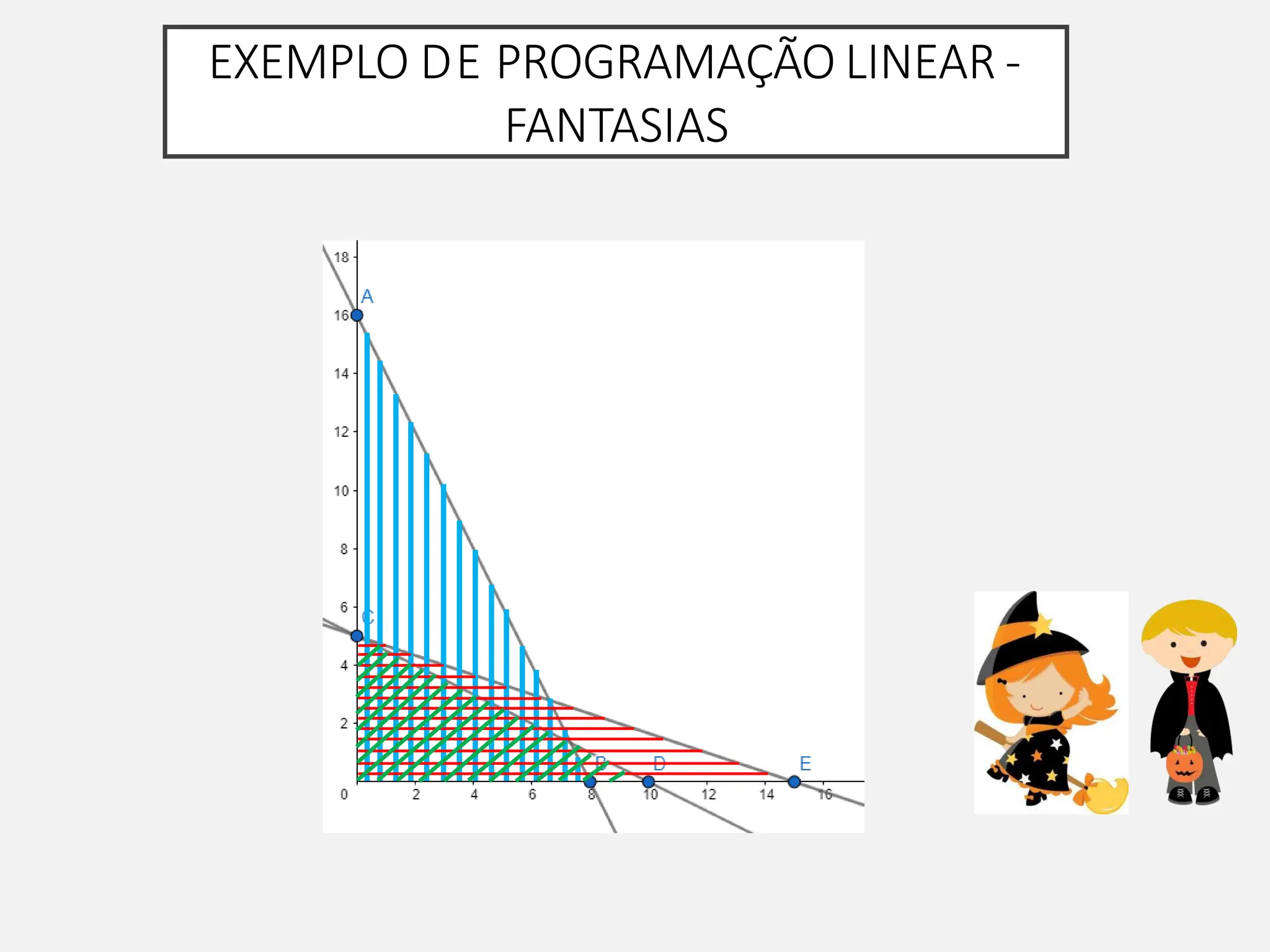
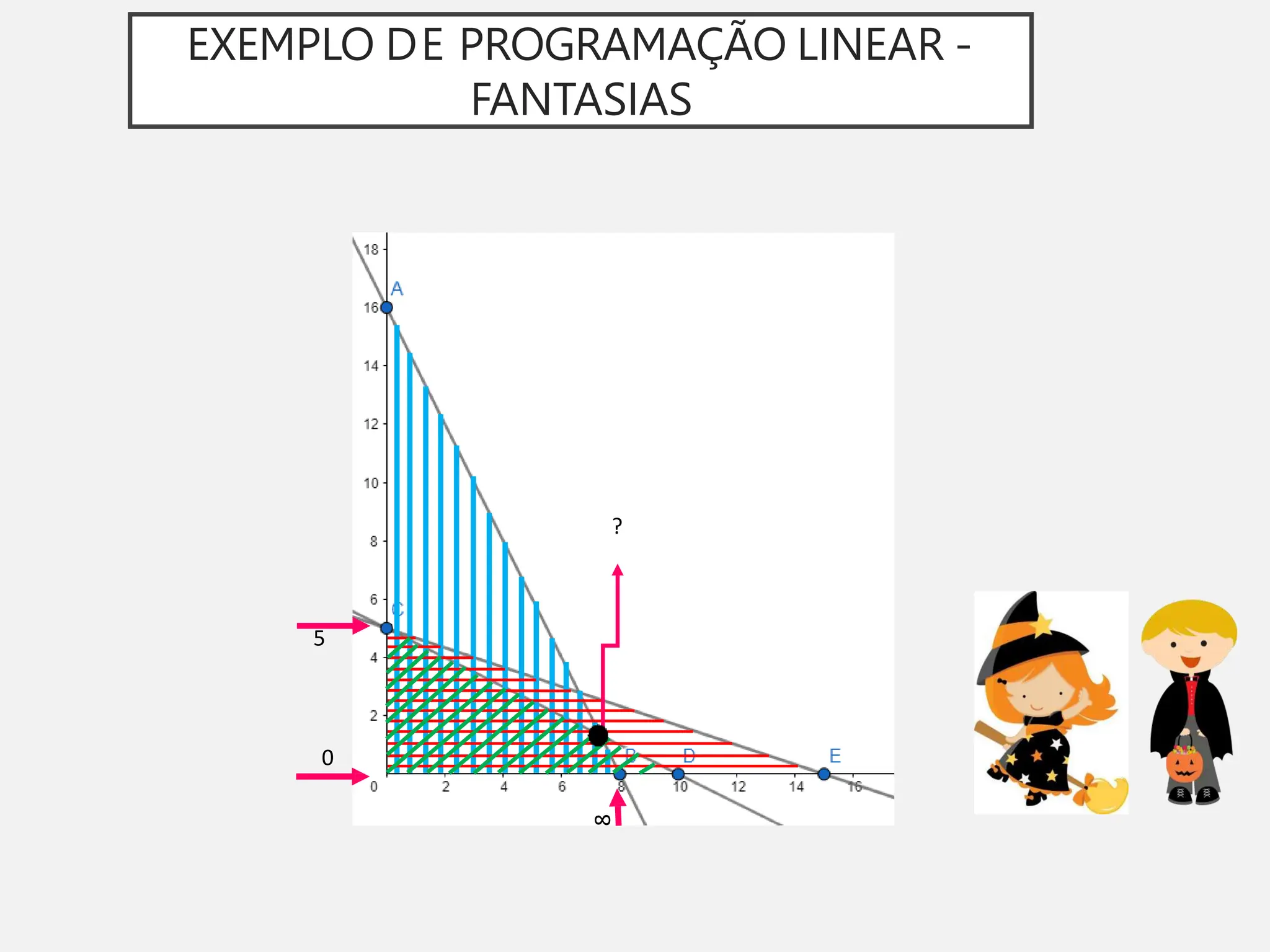
A pesquisa operacional é um método científico de tomada de decisões que utiliza modelos matemáticos para otimizar sistemas. O modelo apresentado utiliza programação linear para maximizar o lucro de um sapateiro, sujeito a restrições de disponibilidade de couro e tempo de produção.

1. Pesquisa Operacional

2. Pesquisa Operacional é um método
científico de tomada de decisões.
Sistema Organizado com o auxílio de
um modelo.
Experimentação modelar com fins de
otimização da operação do sistema.

3. MODELO EM PROGRAMAÇÃO LINEAR
2
1 3
2 x
x 
O modelo matemático é composto de uma função
objetiva linear; e de restrições técnicas representadas
por um grupo de inequações também lineares.
Exemplo:
Função objetivo a ser maximizada:
Lucro =

4. Restrições técnicas:
20
6
10
3
4
2
1
2
1




x
x
x
x
Restrições de não
negatividade:
0
0
2
1


x
x

5. ROTEIRIZAÇÃO
• Variáveis de decisão?
• Objetivo?
• Restrições?

6. Quais as variáveis de decisão?
Programação
de produção
Programação de
investimento
Quantidades a
produzir no período
Decisões de
investimento
Nas descrições sumárias de sistemas, isso
fica claro quando lemos a questão proposta,
isto é, a pergunta do problema.
Problema Variáveis de decisão

7. Quais o objetivo?
Identificar o objetivo da tomada de decisão.
Eles aparecem geralmente na forma da
maximização de lucros ou receitas, minimização de
custos, perdas, etc.
A função objetivo é a expressão que calcula o
valor do objetivo (lucro, custo receita, perda, etc.),
em função das variáveis de decisão.

8. Quais as restrições?
Cada restrição imposta na descrição do sistema
deve ser expressa como uma relação linear
(igualdade ou desigualdade), montadas com as
variáveis de decisão.

9. Exemplo 1:
Certa empresa fabrica dois produtos P1 e P2. O lucro
unitário do produto P1 é de 1.000 unidades monetárias e o
lucro unitário de P2 é de 1.800 unidades monetárias. A
empresa precisa de 20 horas para fabricar uma unidade
de P1 e de 30 horas para fabricar uma unidade de P2. O
tempo anual de produção disponível para isso é de 1.200
horas. A demanda esperada para cada produto é de 40
unidades anuais para P1 e 30 unidades anuais para P2.
Qual é o plano de produção para que a empresa
maximize seu lucro nesses itens?
Construa o modelo de programação linear para esse
caso.

10. Solução:
a) Quais as variáveis de decisão?
O que deve ser decidido é o plano de produção, isto
é, quais as quantidades anuais que devem ser
produzidas de P1 e P2.
Portanto, as variáveis de decisão serão X1 e X2
X1  quantidade anual a produzir de P1
X2  quantidade anual a produzir de P2

11. b) Qual o objetivo?
O objetivo é maximizar o lucro, que pode ser
calculado:
Lucro devido a P1: 1000 . X1 (lucro por unidade de P1 x
quantidade produzida de P1)
Lucro devido a P2: 1800 . X2 (lucro por unidade de P2 x
quantidade produzida de P2)
Lucro total: L = 1000X1 + 1800X2
Objetivo: maximizar L = 1000X1 + 1800X2

12. c) Quais as restrições?
As restrições impostas pelo sistema são:
Disponibilidade de horas para a produção: 1200 horas.
Horas ocupadas com P1: 20X1 (uso por unidade x
quantidade produzida)
Horas ocupadas com P2: 30X2 (uso por unidade x
quantidade produzida)
Total em horas ocupadas na produção:20X1 + 30X2
Disponibilidade: 1200 horas.
Restrição descritiva da situação: 20X1 + 30X2 ≤ 1200

13. Disponibilidade de mercado para os produtos (demanda)
Disponibilidade para P1: 40 unidades
Quantidade a produzir de P1: X1
Restrição descritiva da situação X1 ≤ 40
Disponibilidade para P2: 30 unidades
Quantidade a produzir de P2: X2
Restrição descritiva da situação: X2 ≤ 30

14. Restrições técnicas:
30
40
1200
30
20
2
1
2
1




x
x
x
x
Restrições de não
negatividade:
0
0
2
1


x
x
Resumo do modelo: max L = 1000X1 + 1800X2
Sujeito a:

15. Exemplo 2:
Para uma boa alimentação, o corpo necessita de
vitaminas e proteínas. A necessidade mínima de vitaminas
é de 32 unidades por dia e a de proteínas de 36 unidades
por dia. Uma pessoa tem disponível carne e ovos para se
alimentar. Cada unidade de carne contém 4 unidades de
vitaminas e 6 unidades de proteínas. Cada unidade de
ovo contém 8 unidades de vitaminas e 6 unidades de
proteínas.
Qual a quantidade diária de carne e ovos que deve ser
consumida para suprir as necessidades de vitaminas e
proteínas com o menor custo possível? Cada unidade de
carne custa 3 unidades monetárias e cada unidade de ovo
custa 2,5 unidades monetárias.

16. Solução:
a. Quais as variáveis de decisão?
Devemos decidir quais as quantidades de carne e ovos
a pessoa deve consumir no dia. As variáveis de decisão
serão, portanto:
X1  quantidade de carne a consumir no dia
X2  quantidade de ovos a consumir no dia

17. b. Qual o objetivo?
O objetivo é minimizar o custo, que pode ser calculado:
Custo devido à carne: 3 . X1 (custo por unidade x
quantidade a consumir de carne)
Custo devido aos ovos: 2,5 . X2 (custo por unidade x
quantidade a consumir de ovos)
Custo Total: C = 3X1 + 2,5X2
Objetivo:minimiza C = 3X1 + 2,5X2

18. c. Quais as restrições?
As restrições impostas pelo sistema são:
Necessidade mínima de vitamina: 32 unidades
Vitaminas de carne: 4 . X1 (quantidade por unidade x
unidades de carne a consumir)
Vitamina de ovos: 8 . X2 (quantidade por unidade x
unidades de ovos a consumir)
Total de vitaminas: 4X1 + 8X2
Necessidade mínima: 32
Restrição descritiva da situação: 4X1 + 8X2 ≥ 32

19. Necessidade mínima de proteína: 36 unidades
Proteína de carne: 6 . X1 (quantidade por unidade x
unidades de carne a consumir)
Proteína de ovos: 6 . X2 (quantidade por unidade x
unidades de ovos a consumir)
Total de proteínas: 6X1 + 6X2
Necessidade mínima: 36
Restrição descritiva da situação: 6X1 + 6X2 ≥ 36

20. Restrições técnicas:
36
6
6
32
8
4
2
1
2
1




x
x
x
x Restrições de não
negatividade:
0
0
2
1


x
x
Resumo do modelo: min C = 3X1 + 2,5 X2
Sujeito a:

21. DUAS VARIÁVEIS DE
DECISÃO
Técnica de solução numa
Programação Linear
§ Uma revisão gráfica

22. O desempenho do modelo á avaliado através
da representação gráfica da função objetivo
As soluções são classificadas de acordo com
sua posição no gráfico.
A representação gráfica de uma equação
linear com duas variáveis é uma reta.

23. Exemplo
Representar graficamente a inequação: X1 + 2X2 ≥ 10

24. Exemplo
Representar graficamente a solução do sistema:
X1 + 3X2 ≤ 12
2X1 + X2 ≥ 16
X1 ≥ 0
X2 ≥ 0

26. Método Gráfico
Exemplo: Resolver o problema de programação linear:
Minimizar Z = 2X1 + 3X2
Sujeitos às restrições:
X1 + X2 ≥ 5
5X1 + X2 ≥ 10
X1 ≤ 8
X1 ≥ 0 ; X2 ≥ 0

28. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Um sapateiro faz 6 sapatos por hora, se fizer somente sapatos, e 5 cintos por
hora, se fizer somente cintos. Ele gasta 2 unidades de couro para fabricar 1
unidade de sapato e 1 unidade de couro para fabricar uma unidade de cinto.
Sabendo-se que o total disponível de couro é de 6 unidades e que o lucro
unitário por sapato é de 5 unidades monetárias e o do cinto é de 2 unidades
monetárias, pede-se: o modelo do sistema de produção do sapateiro, se o
objetivo é maximizar seu lucro por hora.

29. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Sapatos – 6 unidades por hora (somente sapatos)
Cintos – 5 unidades por hora (somente cintos)
Total de couro – 6 unidades

30. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Sapatos – 6 unidades por hora (somente sapatos)
Cintos – 5 unidades por hora (somente cintos)
Total de couro – 6 unidades
R$ 5,00
R$ 2,00

31. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Sapatos – 6 unidades por hora (somente sapatos)
Cintos – 5 unidades por hora (somente cintos)
R$ 5,00
R$ 2,00
x1
x2
Total de couro – 6 unidades

32. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Sapatos– 6 unidades por hora (somente sapatos)
Cintos – 5 unidades por hora (somente cintos)
Total de couro – 6 unidades
Função Objetivo: 5x1 + 2x2
Couro Tempo Valor (R$)
X1 2 10 min 5,00
X2 1 12 min 2,00
6 60 min

33. EXEMPLO DE PROGRAMAÇÃO LINEAR -
SAPATEIRO
Cintos – 5 unidades por hora (somente cintos)
Sapatos – 6 unidades por hora (somente sapatos)
Rcouro : 2x1 + x2 <= 6
Total de couro – 6 unidades
Função Objetivo: 5x1 + 2x2
Couro Tempo Valor (R$)
X1 2 10 min 5,00
X2 1 12 min 2,00
6 60 min
Rtempo : 10x1 + 12x2 <= 60
Rnne: x1>=0 e x2>=0

34. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Função Objetivo: 5x1 + 2x2
Rcouro : 2x1 + x2 <= 6 Rtempo : 10x1 + 12x2 <= 60 Rnne: x1>=0 e x2>=0
1 – Encontraras ordenadas (lembrando que agora
eu passo a
chamar x1 de x e x2 de y)
2x + y = 6
y = 6 – 2x
2x + y = 6
2x = 6 – y
x = 6 – y
2
x = 3 – y
2

35. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Função Objetivo: 5x1 + 2x2
Rcouro : 2x1 + x2 <= 6 Rtempo : 10x1 + 12x2 <= 60 Rnne: x1>=0 e x2>=0
1 – Encontraras ordenadas (lembrando que agora
eu passo a chamar x1 de x e x2 de y)
10x + 12y = 60
12y = 60 – 10x
y = 60 – 10x
12 y = 5 – 10x
12
10x + 12y = 60
10x = 60 – 12y
x = 60 – 12y
10
x = 6 – 12y
10

36. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
Função Objetivo: 5x1 + 2x2
2x + y = 6
y = 6 – 2x
2x + y = 6
2x = 6 – y
x = 6 – y
2
x = 3 – y
2
10x + 12y = 60
12y = 60 – 10x
y = 60 – 10x
12 y = 5 – 10x
12
10x + 12y = 60
10x = 60 – 12y
x = 60 – 12y
10
x = 6 – 12y
10

37. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO

38. EXEMPLO DE PROGRAMAÇÃO LINEAR -
SAPATEIRO
5
0
3
x,y

39. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
X Y FO : 5x + 2y
0 0 5.0 + 2.0 = 0
3 0 5.3 + 2.0 = 15
0 5 5.0 + 2.5 = 10
x y
6 – y = 60 – 12y
2 10
10 . (6 – y) = 2 . (60 – 12y)
60 – 10y = 120 – 24y
-10y + 24y = 120 – 60
2x + y = 6
2x + 4,28 = 6
2x = 6 – 4,28
x = 6 – 4,28
2
14y = 60 x = 0,86
y = 4,28

40. EXEMPLO DE PROGRAMAÇÃO LINEAR - SAPATEIRO
X Y FO : 5x + 2y
0 0 5.0 + 2.0 = 0
3 0 5.3 + 2.0 = 15
0 5 5.0 + 2.5 = 10
0,86 4,28 5 . 0,86 + 2 . 4,28 = 12,86
A solução ótima encontrada, é a fabricação de 3 sapatos

41. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
Um carpinteiro dispõe de 90, 80 e 50 metros de compensado, pinho e
cedro, respectivamente. O produto A requer 2, 1 e 1 metro de
compensado, pinho e cedro, respectivamente. O produto B requer 1, 2 e 1
metros, respectivamente. Se A é vendido por R$ 120,00 e B por R$ 110,0,
quantos de cada produto ele deve fazer para obter um rendimento bruto
máximo? Elabore a programação linear.

42. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
90 metros de compensado
80 metros de pinho
50 metros de cedro
Prod. A – 2 metros de compensado
1 metro de pinho
1 metro de cedro
Prod. B– 1 metro de compensado
2 metros de pinho
1 metro de cedro

43. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
90 metros de compensado
80 metros de pinho 50
metros de cedro
Prod. A – 2 metros de compensado
1 metro de pinho 1
metro de cedro
Prod. B– 1 metro de compensado
2 metros de pinho 1
metro de cedro
FO : 120x1 + 110x2

44. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
90 metros de compensado 80 metros
de pinho
50 metros de cedro
Prod. A – 2 metros de
compensado
1 metro de pinho 1 metro de cedro
Prod. B– 1 metro de compensado
2 metros de pinho
1 metro de cedro
FO : 120x1 + 110x2
Compensado Pinho Cedro (R$)
X1 2 1 1 120,00
X2 1 2 1 110,00
90 80 50

45. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
RCo :
RPi :
RCe :
Rnne:
2x1 + x2 <=90
x1 + 2x2 <=80
x1 + x2 <=50
x1>=0 e x2>=0
Compensa
do
Pinho Cedro (R$)
X1 2 1 1 120,00
X2 1 2 1 110,00
90 80 50
90 metros de compensado
80 metros de pinho
50 metros de cedro
Prod. A – 2 metros de compensado
1 metro de pinho 1 metro de cedro
Prod. B– 1 metro de compensado
2 metros de pinho
1 metro de cedro
FO : 120x1 + 110x2

46. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
RCo :
RPi :
RCe :
Rnne:
2x1 + x2 <=90
x1 + 2x2 <=80
x1 + x2 <=50
x1>=0 e x2>=0
1 – Encontrar as ordenadas
2x1 + x2 = 90
x1 = 0
X2 = 90/1 = 90
2x1 + x2 = 90
x2 = 0
x1= 90/2 = 45
x1 + 2x2 = 80
x1 = 0
X2 = 80/2 = 40
2x1 + x2 = 90
x2 = 0
x1= 80/1 = 80
x1 + x2 = 50
x1 = 0
X2 = 50/1 = 50
x1 + x2 = 50
x2 = 0
x1= 50/1 = 50
FO : 120x1 + 110x2

47. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA

48. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
40
0
45
(1)
(2)

49. RESOLUÇÃO DA SITUAÇÃO
PROBLEMA
x1 x2 FO : 120x1 + 110x2
0 0 120*0 + 110*0 = 0
45 0 120*45 + 110*0 = 5400
0 40 120*0 + 110*40 = 4400
20 30 120*20 + 110*30 = 5700
40 10 120*40 + 110*10 = 5900
(1)
(2)
Interseção do ponto (1) (Rpi - Rce)
x1 + 2x2 =80 x1 + 2(30) = 80
x1 + x2 =50 (-1) x1 + 60 = 80
x1 = 80 - 60
x1 + 2x2 =80 x1 = 20
-x1 - x2 = - 50
= x2 = 80 + (-50)
X2 = 30
Interseção do ponto (2) (Rco - Rce)
2x1 + x2 = 90 x1 + 1(40) = 50
x1 + x2 =50 (-2) x1 + 40 = 50
x1 = 50 - 40
2x1 + x2 = 90 x1 = 10
-2x1 - 2x2 = - 100
= -2x2 = 90 + (-50)
X2 = -x2 = -40
X2 = 40

50. EXEMPLO DE PROGRAMAÇÃO LINEAR -
FANTASIAS

51. EXEMPLO DE PROGRAMAÇÃO LINEAR - FANTASIAS
Um fabricante de fantasias tem em estoque 32 m de brim, 20 m de seda e 30 m de
cetim e pretende fabricar dois modelos de fantasias. O primeiro modelo (M1)
consome 4m de brim, 2 m de seda e 2 m de cetim. O segundo modelo (M2)
consome 2 m de brim, 4 m de seda e 6 m de cetim. Se M1 é vendido a R$ 60,00 e
M2 a R$ 100,00, quantas peças de cada tipo o fabricante deve fazer para obter a
receita máxima? Elabore o modelo.

52. EXEMPLO DE PROGRAMAÇÃO LINEAR - FANTASIAS
32 metros de brim
20 metros de seda
30 metros de cetim
Modelo 1– 4 metros de brim
2 metros de seda
2 metros de cetim
Modelo 2– 2 metros de brim
4 metros de seda
6 metros de cetim

53. EXEMPLO DE PROGRAMAÇÃO LINEAR - FANTASIAS
32 metros de brim
20 metros de seda
30 metros de cetim
Modelo 1– 4 metros de brim
2 metros de seda
2 metros de cetim
Modelo 2– 2 metros de brim
4 metros de seda
6 metros de cetim
FO : 60x1 + 100x2

54. EXEMPLO DE PROGRAMAÇÃO LINEAR - FANTASIAS
32 metros de brim
20 metros de seda
30 metros de cetim
Modelo 1– 4 metros de brim
2 metros de seda
2 metros de cetim
Modelo 2– 2 metros de brim
4 metros de seda
6 metros de cetim
FO : 60x1 + 100x2
Modelo 1 Modelo 2 Total
Brim 4 2 32
Seda 2 4 20
Cetim 2 6 30
RB : 4x1 + 2x2 <=32
1 2
R : 2x + 4x <=20
S
RC : 2x1 + 6x2 <=30
Rnne: x1>=0 e x2>=0

55. EXEMPLO DE PROGRAMAÇÃO LINEAR - FANTASIAS
RB : 4x1 + 2x2 <=32 RS : 2x1 + 4x2 <=20 RC : 2x1 + 6x2 <=30
Rnne: x1>=0 e x2>=0
1 – Encontrar as ordenadas (lembrando que agora eu passo a chamar x1 de x e x2 de y)
FO : 60x1 + 100x2
4x1 + 2x2 = 32
x1 = 0
x2 = 32/2 = 16
x2 = 0
x1= 32/4 = 8
2x1 + 4x2 = 20
x1 = 0
x2 = 20/4 = 5
x2 = 0
x1= 20/2 = 10
2x1 + 6x2 = 30
x1 = 0
x2 = 30/6 = 5
x2 = 0
x1= 30/2 = 15

56. EXEMPLO DE PROGRAMAÇÃO LINEAR -
FANTASIAS

57. EXEMPLO DE PROGRAMAÇÃO LINEAR -
FANTASIAS
5
0
8
?

58. EXEMPLO DE PROGRAMAÇÃO LINEAR -
FANTASIAS
x1 x2 FO : 60x1 + 100x2
0 0 60*0 + 100*0 = 0
8 0 60*8 + 100*0 = 480
0 5 60*0 + 100*5 = 500
x1 x2 60*7,33 + 100*1,34 = 573,80
Interseção do ponto (1) (Rb - Rs)
4x1 + 2x2 = 32
2x1 + 4x2 = 20
2x1 = 20 – 4x2
X1 = 20 – 4x2/2