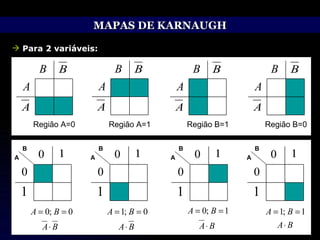
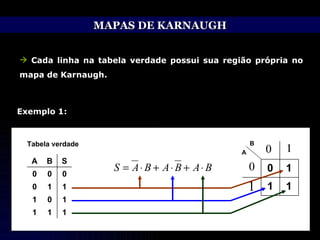
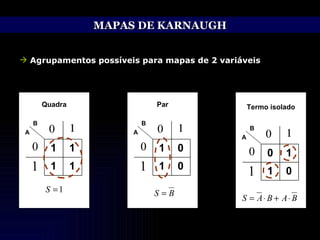
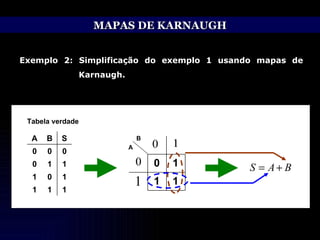
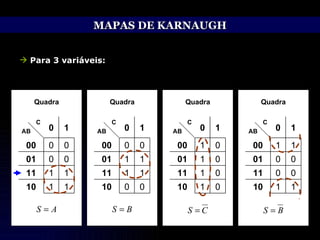
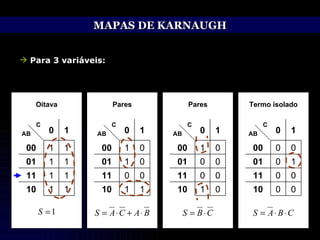
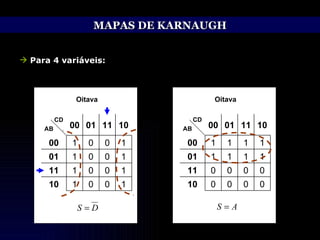
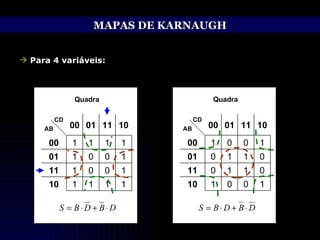
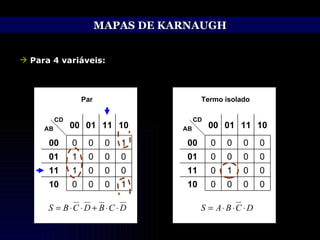
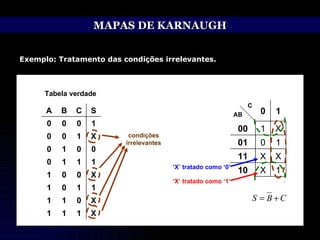
O documento discute técnicas de simplificação de circuitos lógicos digitais utilizando a álgebra de Boole e mapas de Karnaugh. Apresenta identidades e propriedades da álgebra de Boole que permitem simplificar equações lógicas, como os teoremas de Morgan. Também explica o método dos mapas de Karnaugh, que permite representar graficamente equações de até 5 variáveis e simplificá-las, agrupando termos adjacentes. Aborda ainda o tratamento de condições lógicas irrelevantes nos mapas.

1. ELETRÔNICA DIGITAL Parte II – Simplificação de circuitos lógicos Prof. Matheus Ribeiro

2. SIMPLIFICAÇÃO DE CIRCUITOS LÓGICOS Até aqui trabalhamos com circuitos lógicos sem nos preocuparmos com a sua complexidade ou número de portas utilizadas. No entanto, na maioria dos casos os circuitos podem ser simplificados. Analisando os postulados da álgebra de Boole, chegamos a um conjunto de identidades e propriedades que permitem a simplificação dos circuitos:

3. IDENTIDADES DA ÁLGEBRA DE BOOLE MULTIPLICAÇÃO ADIÇÃO COMPLEMENTAÇÃO

4. PROPRIEDADES DA ÁLGEBRA DE BOOLE

5. TEOREMAS DE MORGAN O complemento do produto é igual à soma dos complementos: prova O complemento da soma é igual ao produto dos complementos: prova A B 0 0 0 1 1 0 1 1 1 0 0 0 1 0 0 0 A B 0 0 0 1 1 0 1 1 1 1 1 0 1 1 1 0

6. IDENTIDADES AUXILIARES 1 A 1 0

7. SIMPLIFICAÇÃO DE EQUAÇÕES BOOLEANAS A) Usando os teoremas e propriedades da álgebra Booleana vistos até aqui. B) Usando os mapas de Karnaugh, também chamado de método gráfico.

8. MAPAS DE KARNAUGH Para 2 variáveis: Região A=0 Região A=1 Região B=1 Região B=0 B A B A B A B A

9. MAPAS DE KARNAUGH Cada linha na tabela verdade possui sua região própria no mapa de Karnaugh. Exemplo 1: Tabela verdade 1 1 1 0 B A 1 1 1 1 0 1 1 1 0 0 0 0 S B A

10. MAPAS DE KARNAUGH Agrupamentos possíveis para mapas de 2 variáveis Quadra Termo isolado Par 1 1 1 1 B A 0 1 1 0 B A 0 1 0 1 B A

11. MAPAS DE KARNAUGH Exemplo 2: Simplificação do exemplo 1 usando mapas de Karnaugh. Tabela verdade 1 1 1 0 B A 1 1 1 1 0 1 1 1 0 0 0 0 S B A

12. MAPAS DE KARNAUGH Para 3 variáveis: Quadra Quadra Quadra Quadra 0 1 1 0 0 0 10 1 11 1 01 0 00 1 C AB 1 1 1 1 0 0 10 0 11 0 01 0 00 1 C AB 1 1 0 0 0 1 10 1 11 0 01 0 00 1 C AB 1 0 0 1 0 1 10 0 11 0 01 1 00 1 C AB

13. MAPAS DE KARNAUGH Para 3 variáveis: Oitava Pares Pares Termo isolado 1 1 1 1 0 1 10 1 11 1 01 1 00 1 C AB 1 0 1 1 0 1 10 0 11 0 01 0 00 1 C AB 1 0 0 1 0 0 10 0 11 0 01 0 00 1 C AB 0 0 0 0 0 0 10 0 11 1 01 0 00 1 C AB

14. MAPAS DE KARNAUGH Para 4 variáveis: Oitava Oitava 0 0 0 0 01 0 0 0 0 11 1 1 1 1 00 1 10 1 11 1 01 1 00 10 CD AB 0 0 1 1 01 0 0 1 1 11 0 0 1 1 00 0 10 0 11 1 01 1 00 10 CD AB

15. MAPAS DE KARNAUGH Para 4 variáveis: Quadra Quadra 1 0 0 1 01 1 0 0 1 11 1 1 1 1 00 1 10 1 11 1 01 1 00 10 CD AB 0 1 1 0 01 0 1 1 0 11 1 0 0 1 00 1 10 0 11 0 01 1 00 10 CD AB

16. MAPAS DE KARNAUGH Para 4 variáveis: Par Termo isolado 0 0 0 0 01 0 0 0 0 11 0 1 1 0 00 1 10 0 11 0 01 1 00 10 CD AB 0 1 0 0 01 0 0 0 0 11 0 0 0 0 00 0 10 0 11 0 01 0 00 10 CD AB

17. MAPAS DE KARNAUGH Para 5 variáveis: 0 0 1 0 010 0 0 0 0 110 0 1 0 0 111 0 0 0 0 101 1 0 0 0 100 0 0 0 0 001 0 1 0 0 011 1 0 1 0 000 10 11 01 00 CDE AB

18. MAPAS DE KARNAUGH Condições irrelevantes São as situações de entrada para as quais a saída pode assumir qualquer nível lógico. Ocorrem, principalmente, na impossibilidade prática do caso de entrada acontecer e são representadas pelo símbolo ‘X’. No mapa de Karnaugh, pode-se usar ‘0’ ou ‘1’ para a condição irrelevante de forma a promover maior simplificação.

19. MAPAS DE KARNAUGH Exemplo: Tratamento das condições irrelevantes. Tabela verdade ‘ X’ tratado como ‘0’ ‘ X’ tratado como ‘1’ condições irrelevantes X X 0 1 0 1 10 X 11 1 01 X 00 1 C AB 1 1 1 0 X 0 0 1 1 1 0 1 X 0 1 1 1 0 1 0 C X 1 1 0 1 0 X 0 0 1 0 0 S B A