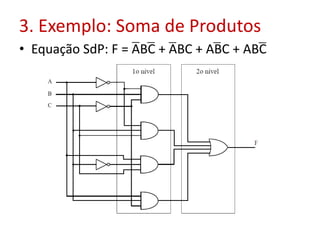
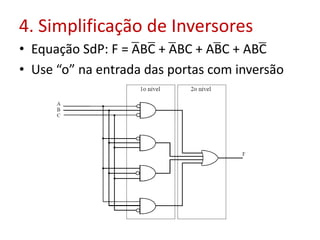
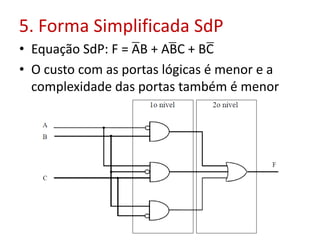
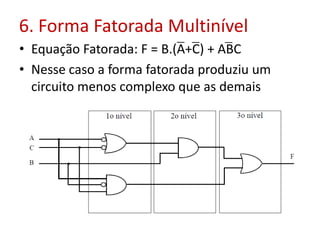
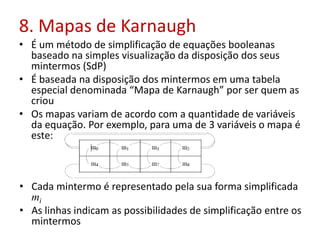
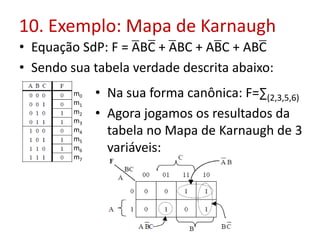
O documento discute fundamentos de circuitos lógicos, incluindo tipos de circuitos lógicos (de dois níveis e multiníveis), exemplo de soma de produtos, simplificação de inversores, formas simplificadas e fatoradas, complexidade de circuitos e uso de mapas de Karnaugh para simplificação de equações booleanas.

1. Aula 008
Fundamentos da
Informática
PRONATEC
Programa Nacional de Acesso ao
Ensino Técnico e Emprego

2. PRONATEC
Programa Nacional de Acesso
ao Ensino Técnico e Emprego

3. 1. Circuitos Lógicos
• A partir da equação o projetista elétrico deve
desenhar os circuitos observando o seguinte:
• 1) As variáveis de entrada ficam sempre a
esquerda junto aos respectivos fios
• 2) Inversores devem ser desenhados para as
variáveis negadas
• 3) As portas lógicas devem ser desenhadas da
esquerda para a direita, sendo as mais a esquerda
com prioridade maior de acordo com as regras
matemáticas
• 4) Se dois fios se conectam deve ser representado
com um ponto mais forte indicando “solda”, sem
esse ponto indica que estão isolados

4. 2. Tipos de Circuitos Lógicos
• Circuito de Dois Níveis (ou Lógica a Dois
Níveis): são circuitos que representam as
equações da forma padrão, canônica ou
simplificadas, isto é, aquelas derivadas de
mintermos (SdP) e maxitermos (PdS).
• Circuitos Multinível (ou Lógica Multinível): são
circuitos que representam as equações
fatoradas, onde não há definido mintermos ou
maxtermos.

5. 3. Exemplo: Soma de Produtos
• Equação SdP: F = ABC + ABC + ABC + ABC

6. 4. Simplificação de Inversores
• Equação SdP: F = ABC + ABC + ABC + ABC
• Use “o” na entrada das portas com inversão

7. 5. Forma Simplificada SdP
• Equação SdP: F = AB + ABC + BC
• O custo com as portas lógicas é menor e a
complexidade das portas também é menor

8. 6. Forma Fatorada Multinível
• Equação Fatorada: F = B.(A+C) + ABC
• Nesse caso a forma fatorada produziu um
circuito menos complexo que as demais

9. 7. Complexidade dos Circuitos
• Uma equação mínima sempre terá menor complexidade
relativa que sua forma canônica
• A medida da complexidade relativa de um circuito é
calculada pela quantidade de entradas em cada porta do
mesmo. Assim no exemplo da forma padrão temos 4
portas E com 3 entradas cada mais uma porta OU com 4
entradas, total de 4x3+1x4=16 entradas. Na forma
mínima temos 2 portas de 2 entradas e duas de 3
entradas, total de 2x2+2x3=10 entradas. Já na forma
fatorada temos 3 portas de 2 e 1 de 3, então 9 portas,
tornando o circuito fatorado o de menor complexidade
• Algumas vezes, a forma fatorada produz circuitos menos
complexos que a forma mínima como no exemplo
mostrado. A forma de saber o melhor circuito é
desenhar todas as formas e então calcular o número de
entradas de cada um, o menor é o menos complexo.

10. 8. Mapas de Karnaugh
• É um método de simplificação de equações booleanas
baseado na simples visualização da disposição dos seus
mintermos (SdP)
• É baseada na disposição dos mintermos em uma tabela
especial denominada “Mapa de Karnaugh” por ser quem as
criou
• Os mapas variam de acordo com a quantidade de variáveis
da equação. Por exemplo, para uma de 3 variáveis o mapa é
este:
• Cada mintermo é representado pela sua forma simplificada
mi
• As linhas indicam as possibilidades de simplificação entre os
mintermos

11. 9. Uso do Mapa de Karnaugh
• Para usar o Mapa é simples, devemos montar a
tabela verdade para a equação dentro dele
• Depois deve-se identificar todos os mintermos-
1 adjacentes entre si circulando-os
• Por fim deve-se escolher as variáveis
correspondentes na tabela aos mintermos-1
adjacentes e fazer um OU(+) lógico entre elas

12. 10. Exemplo: Mapa de Karnaugh
• Equação SdP: F = ABC + ABC + ABC + ABC
• Sendo sua tabela verdade descrita abaixo:
• Na sua forma canônica: F=∑(2,3,5,6)
• Agora jogamos os resultados da
tabela no Mapa de Karnaugh de 3
variáveis:
m0
m1
m2
m3
m4
m5
m6
m7

13. 11. Exemplo: M.Karnaugh (cont.)
• Equação SdP: F = ABC + ABC + ABC + ABC
• Então circula-se os
mintermos-1 adjacentes
• Mintermos-1 são aqueles
cujo valor resultado da
equação vale “1”
• A simplificação é feita com um OU(+) lógico
entre as variáveis comuns dos mintermos-1
adjacentes. Nesse exemplo fica assim:
• F = AB + BC + ABC
• Que foi o resultado obtido matematicamente