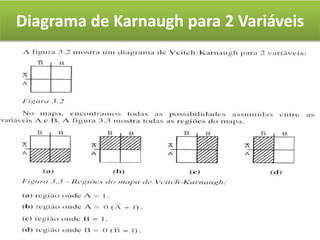
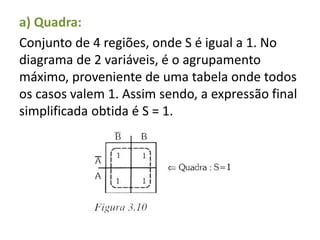
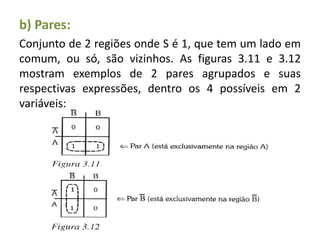
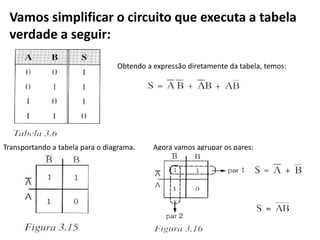
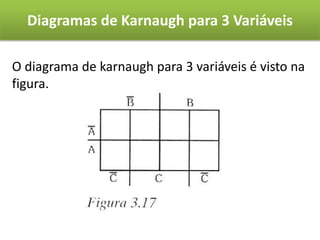
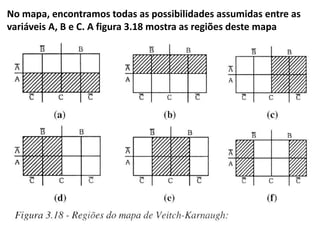
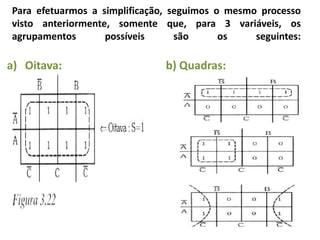
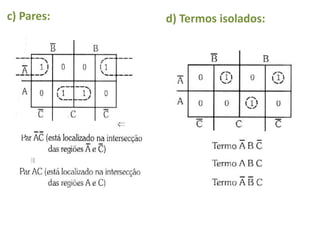
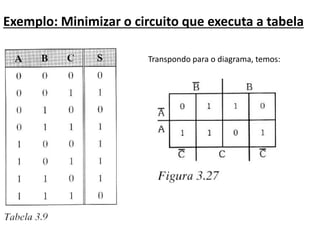
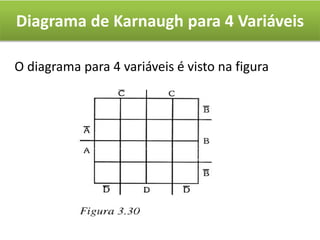
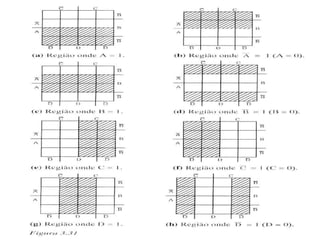
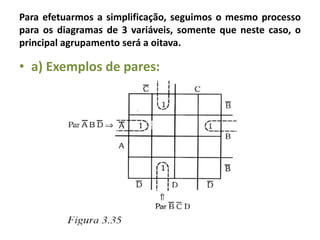
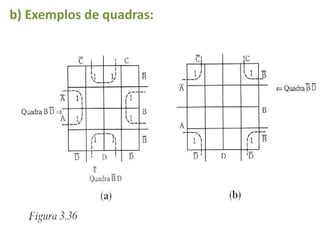
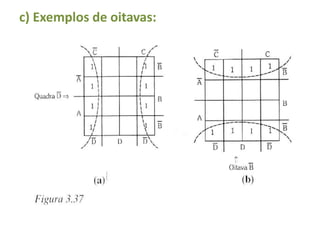
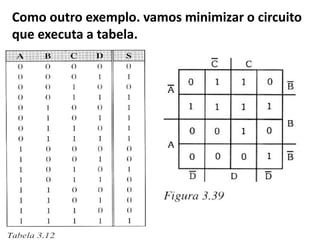
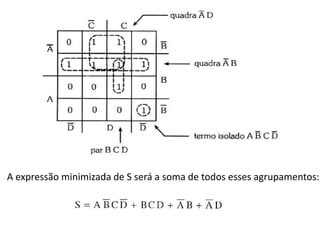
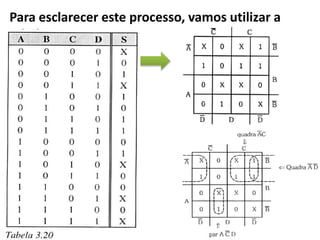
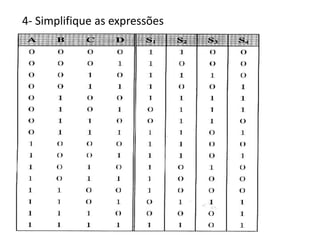
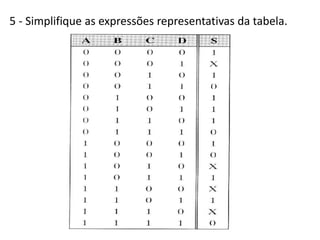
O documento descreve o método de mapas de Veitch-Karnaugh para simplificar funções lógicas. Ele explica como construir diagramas de Karnaugh para 2, 3 e 4 variáveis e como agrupar regiões para obter expressões simplificadas. Também discute como lidar com condições irrelevantes nos diagramas e fornece exercícios de fixação.

1. Mapas de Veitch-Karnaugh
Docente: Sousa Silva

2. O QUE SERIA?
• É um método de simplificação gráfico criado
por Edward Veitch (1952) e aperfeiçoado pelo
engenheiro de telecomunicações Maurice
Karnaugh. Chamamos esse diagrama de
mapa, visto este ser um mapeamento
biunívoco a partir de uma tabela verdade da
função que está a ser analisada.

3. Função do método
• Ele é utilizado para simplificar uma equação
lógica ou para converter uma tabela verdade
no seu circuito lógico correspondente.
• O método de leitura por "mapa de Karnaugh“
elimina o problema de erro nas simplificações.
Porém quando utilizado mais de 6 entradas,
esse método se torna complicado, pois fica
difícil identificar as células adjacentes no
mapa.

4. Diagrama de Karnaugh para 2 Variáveis

7. Como obter as expressões?!
Para obtermos a expressão simplificada do
diagrama, utilizamos o seguinte metodo:
Tentamos agrupar as regiões onde S é igual a 1,
no menor número possível de agrupamentos. As
regiões onde S é 1, que não puderem ser
agrupadas, serão consideradas isoladamente.
Para um diagrama de 2 variáveis, os
agrupamentos possíveis são os seguintes:

8. a) Quadra:
Conjunto de 4 regiões, onde S é igual a 1. No
diagrama de 2 variáveis, é o agrupamento
máximo, proveniente de uma tabela onde todos
os casos valem 1. Assim sendo, a expressão final
simplificada obtida é S = 1.

9. b) Pares:
Conjunto de 2 regiões onde S é 1, que tem um lado em
comum, ou só, são vizinhos. As figuras 3.11 e 3.12
mostram exemplos de 2 pares agrupados e suas
respectivas expressões, dentro os 4 possíveis em 2
variáveis:

10. c) Termos isolados:
Regiões onde S é 1, sem vizinhança para grupamentos.
São os próprios casos de entrada, sem simplificação. A
figura 3.13 exemplifica 2 termos isolados, sem
possibilidade de agrupamento.

11. Vamos simplificar o circuito que executa a tabela
verdade a seguir:
Transportando a tabela para o diagrama.
Obtendo a expressão diretamente da tabela, temos:
Agora vamos agrupar os pares:

12. Diagramas de Karnaugh para 3 Variáveis
O diagrama de karnaugh para 3 variáveis é visto na
figura.

13. No mapa, encontramos todas as possibilidades assumidas entre as
variáveis A, B e C. A figura 3.18 mostra as regiões deste mapa

14. Para efetuarmos a simplificação, seguimos o mesmo processo
visto anteriormente, somente que, para 3 variáveis, os
agrupamentos possíveis são os seguintes:
a) Oitava: b) Quadras:

15. c) Pares: d) Termos isolados:

16. Exemplo: Minimizar o circuito que executa a tabela
Transpondo para o diagrama, temos:

17. Diagrama de Karnaugh para 4 Variáveis
O diagrama para 4 variáveis é visto na figura

19. Para efetuarmos a simplificação, seguimos o mesmo processo
para os diagramas de 3 variáveis, somente que neste caso, o
principal agrupamento será a oitava.
• a) Exemplos de pares:

20. b) Exemplos de quadras:

21. c) Exemplos de oitavas:

22. Como outro exemplo. vamos minimizar o circuito
que executa a tabela.

23. A expressão minimizada de S será a soma de todos esses agrupamentos:

24. Diagramas com Condições Irrelevantes
Chamamos de condição irrelevante (X) a
situação de entrada onde a saída pode assumir 0 ou
1 indiferentemente.
Esta condição ocorre principalmente pela
impossibilidade prática do caso de entrada
acontecer, para sua utilização em diagramas de
Veitch-Karnaugh, devemos, para cada condição
irrelevante, adotar 0 ou 1, dos dois, aquele que
possibilitar melhor agrupamento e
consequentemente maior simplificação.

25. Para esclarecer este processo, vamos utilizar a
tabela

26. Exercícios de fixação
1- Simplifique as expressões obtidas das tabelas a
seguir, utilizando os diagramas de Karnaugh.

27. 2- Simplifique as expressões obtidas das tabelas a
seguir, utilizando os diagramas de Kamaugh.

28. 3- Simplifique as expressões obtidas utilizando os
diagramas de Kamaugh.

29. 4- Simplifique as expressões

30. 5 - Simplifique as expressões representativas da tabela.