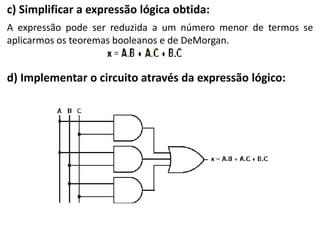
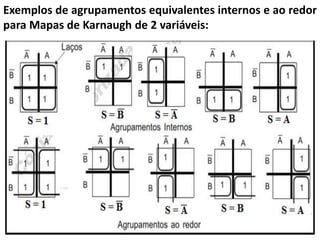
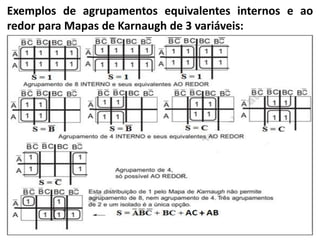
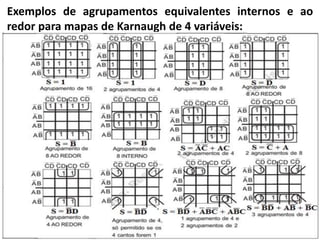
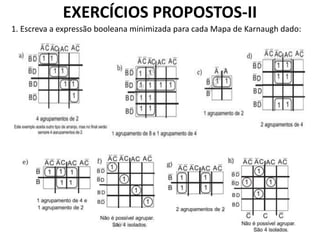
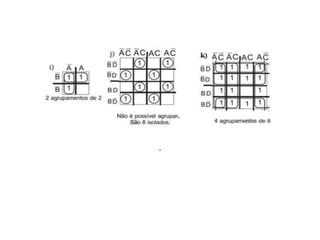
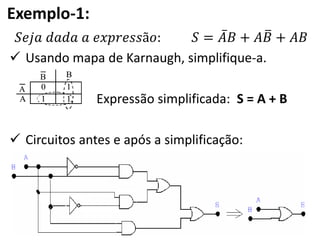
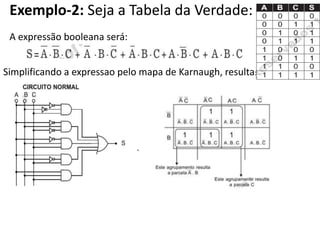
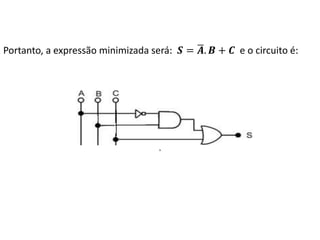
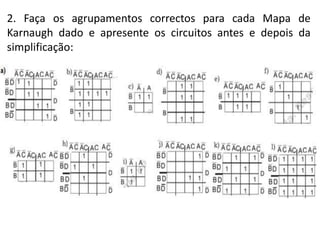
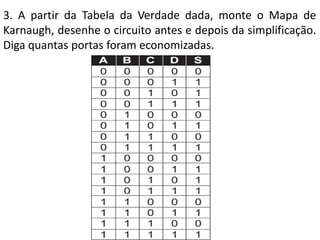
1) O documento descreve os passos para projetar circuitos lógicos, incluindo montar a tabela-verdade, analisar a saída, simplificar a expressão lógica e implementar o circuito. 2) É explicado como os diagramas de Veitch-Karnaugh permitem simplificar expressões lógicas com agrupamentos de potências de 2 células vizinhas. Exemplos ilustram agrupamentos válidos. 3) Dois exemplos mostram como simplificar expressões lógicas usando mapas de Karnaugh e comparar circuit

1. INSTITUTO SUPERIOR DE GESTAO DE CIENCIAS E TECNOLOGIAS
ELECTRÓNICA DIGITAL
AULA-3
Docente: Eng. Sérgio Sambo, MSc

2. Projectando Circuitos Lógicos
Passos para o projecto completo de um circuito lógico:
a) Montar a tabela-verdade:
b) Analisar a saída:
• Quando qualquer entrada de uma porta OR for “1” então a saída será “1”.
Então podemos deduzir que a saída x é uma operação OR de todos os
casos em que a saída x é “1”. Cada caso corresponde a uma operação
lógica AND com todas as variáveis de entrada.

3. c) Simplificar a expressão lógica obtida:
A expressão pode ser reduzida a um número menor de termos se
aplicarmos os teoremas booleanos e de DeMorgan.
d) Implementar o circuito através da expressão lógico:

4. Simplificação de circuitos lógicos usando o Diagrama de
Veitch-Karnaugh
 Os Diagrama de Veitch-Karnaugh Permitem a
simplificação de expressões lógicas com 2, 3, 4, 5
ou mais variáveis. No diagrama só são permitidos
agrupamentos de 1, 2, 4, 8, 16, 32, 64, etc, isto é,
potências de 2. Exemplos:

5. Exemplos de agrupamentos equivalentes internos e ao redor
para Mapas de Karnaugh de 2 variáveis:

6. Exemplos de agrupamentos equivalentes internos e ao
redor para Mapas de Karnaugh de 3 variáveis:

7. Exemplos de agrupamentos equivalentes internos e ao
redor para mapas de Karnaugh de 4 variáveis:

8. Resumindo: os agrupamentos devem
ser de células vizinhas ou ao redor,
formando blocos de 16, 8, 4, 2, ou
isolado. Sempre tentamos agrupar o
máximo possível dentro destas regras
e exemplos vistos.
.

9. Exemplo-1:
𝑆𝑒𝑗𝑎 𝑑𝑎𝑑𝑎 𝑎 𝑒𝑥𝑝𝑟𝑒𝑠𝑠ã𝑜: 𝑆 = 𝐴𝐵 + 𝐴𝐵 + 𝐴𝐵
 Usando mapa de Karnaugh, simplifique-a.
Expressão simplificada: S = A + B
 Circuitos antes e após a simplificação:

10. Exemplo-2: Seja a Tabela da Verdade:
.
A expressão booleana será:
Simplificando a expressao pelo mapa de Karnaugh, resulta:

11. Portanto, a expressão minimizada será: 𝑺 = 𝑨. 𝑩 + 𝑪 e o circuito é:
.

12. EXERCÍCIOS PROPOSTOS-II
1. Escreva a expressão booleana minimizada para cada Mapa de Karnaugh dado:

13. .
.

14. 2. Faça os agrupamentos correctos para cada Mapa de
Karnaugh dado e apresente os circuitos antes e depois da
simplificação:
.

15. 3. A partir da Tabela da Verdade dada, monte o Mapa de
Karnaugh, desenhe o circuito antes e depois da simplificação.
Diga quantas portas foram economizadas.
.

16. FIM
…