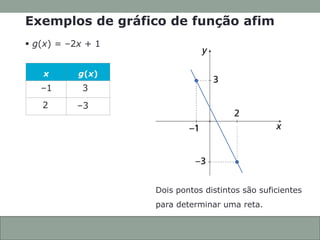
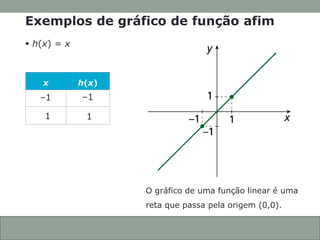
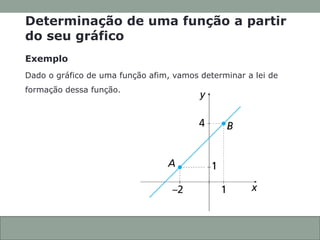
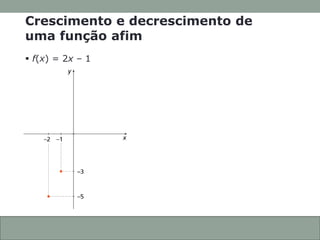
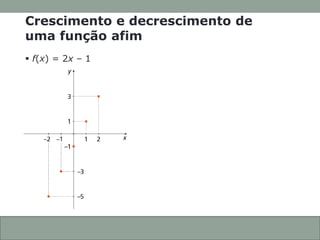
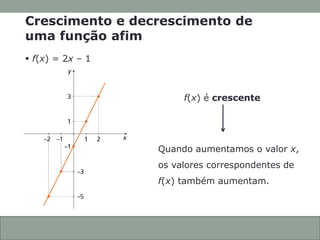
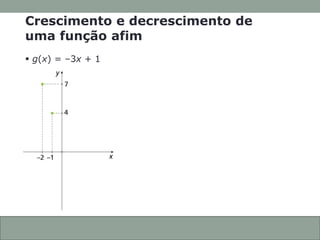
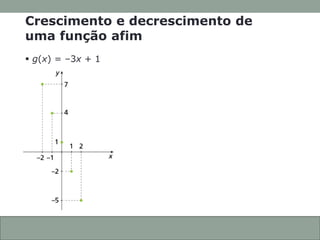
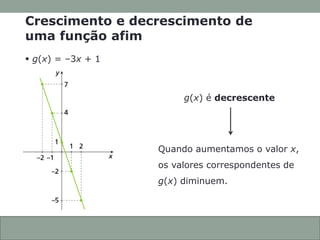
O documento discute funções afins, incluindo: (1) como construir gráficos de funções afins a partir de pontos; (2) como determinar a função a partir de seu gráfico; e (3) como identificar se uma função afim é crescente ou decrescente com base em seu coeficiente angular.
2. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
Gráfico da função afim
Construção do gráfico
Como exemplo, vamos construir o gráfico da função
f(x) = 3x – 2.
3.6
x f(x)
–1 –5
0
2
3
2 4
0 –2
1 1
3. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
3.6
Gráfico da função afim
Construção do gráfico
x f(x)
–1 –5
0
2
3
2 4
0 –2
1 1
Como exemplo, vamos construir o gráfico da função
f(x) = 3x – 2.
4. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
g(x) = –2x + 1
Dois pontos distintos são suficientes
para determinar uma reta.
Exemplos de gráfico de função afim
3.7
x g(x)
–1 3
2 –3
5. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
f(x) = 3
O gráfico de uma função constante é uma reta
paralela ao eixo x, por isso podemos traçá-la
conhecendo um único ponto.
Exemplos de gráfico de função afim
3.7
x f(x)
1 3
6. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
O gráfico de uma função linear é uma
reta que passa pela origem (0,0).
Exemplos de gráfico de função afim
h(x) = x
3.7
x h(x)
–1 –1
1 1
7. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
Determinação de uma função a partir
do seu gráfico
Dado o gráfico de uma função afim, vamos determinar a lei de
formação dessa função.
Exemplo
3.8
8. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
A(–2, 1)
Portanto: f(x) = x + 3
3.8
2a + b = 1
a + b = 4
⇒ a = 1 e b = 3
B(1, 4)
1 = a ∙ (–2) + b
x = –2 e y = 1
4 = a ∙ (1) + b
x = 1 e y = 4
Então:
Determinação de uma função a partir
do seu gráfico
Exemplo
9. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
Exercício resolvido
R2. Determinar o ponto de intersecção das retas
correspondentes aos gráficos das funções afins
f(x) = 4x + 11 e g(x) = –x + 1.
Resolução
Para que as retas tenham um ponto em comum, deve existir
um valor de x de modo que as imagens desse valor pelas
duas funções coincidam, ou seja, f(x) = g(x).
4x + 11 = –x + 1 5x = –10 x = –2
3.9
10. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
Para x = –2, temos: f(–2) = g(–2) = 3
Logo, o ponto de intersecção é (–2, 3).
3.9
R2. Determinar o ponto de intersecção das retas
correspondentes aos gráficos das funções afins
f(x) = 4x + 11 e g(x) = –x + 1.
Resolução
Exercício resolvido
13. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
f(x) é crescente
Quando aumentamos o valor x,
os valores correspondentes de
f(x) também aumentam.
3.15
Crescimento e decrescimento de
uma função afim
f(x) = 2x – 1
16. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
g(x) é decrescente
Quando aumentamos o valor x,
os valores correspondentes de
g(x) diminuem.
3.16
g(x) = –3x + 1
Crescimento e decrescimento de
uma função afim
17. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
Função crescente (a > 0)
x2 > x1 ax2 + b > ax1 + b,
ou seja, f(x2) > f(x1)
3.17
Crescimento e decrescimento de
uma função afim
18. CONEXÕES COM
A MATEMÁTICA
ANOTAÇÕES EM AULA
Capítulo 3 – Função afim
Função decrescente (a < 0)
3.17
x2 > x1 ax2 + b < ax1 + b,
ou seja, f(x2) < f(x1)
Crescimento e decrescimento de
uma função afim
