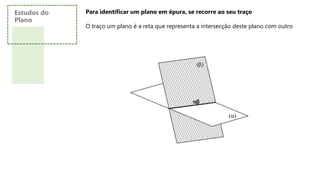
Este documento discute os conceitos básicos de geometria descritiva, incluindo como identificar e representar diferentes tipos de planos em épura. Explica como os planos se interceptam com os planos de projeção e fornece exemplos de exercícios para representar planos horizontais, frontais, de topo, verticais, de perfil, de rampa e planos que passam pela linha de terra.

1. Geometria Descritiva
Estudos do Plano
Prof. Me. Lucas Reitz

2. Para identificar um plano em épura, se recorre ao seu traço
O traço um plano é a reta que representa a intersecção deste plano com outro
Estudos do
Plano

3. Na intersecção de um plano com os planos de projeção vertical e horizontal, se
adota o nome do plano seguido do plano que este intercepta para seus traços
Estudos do
Plano

4. Posições Particulares dos Planos
Plano Horizontal
Paralelo ao plano horizontal; apresenta apenas traço vertical
Estudos do
Plano
Exercício 1 – Representar o plano horizontal α em épura sabendo que sua
cota é 6
b) Na mesma épura, representar o plano β de cota -8.

5. Posições Particulares dos Planos
Plano Frontal
Paralelo ao plano vertical; apresenta apenas traço horizontal
Estudos do
Plano
Exercício 2 – Representar o plano frontal β em épura sabendo que seu
afastamento é 6
b) Na mesma épura, representar um plano frontal de afastamento -7

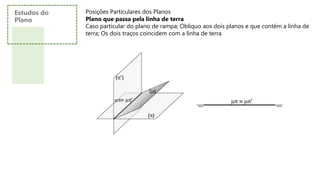
6. Posições Particulares dos Planos
Plano de topo
Perpendicular ao plano vertical e obliquo ao plano horizontal; apresenta dois traços
Estudos do
Plano
Exercício 3 – Representar o plano de topo µ em épura sabendo que seu
traço vertical coincide com a reta AB. (A) [1, 0, 0]; (B) [12, 0, 14]

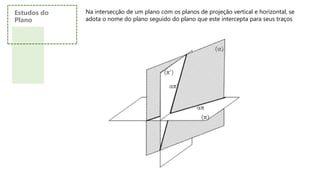
7. Posições Particulares dos Planos
Plano Vertical
Perpendicular ao plano horizontal e obliquo ao plano vertical; apresenta dois traços
Estudos do
Plano
Exercício 4 – Representar o plano vertical α em épura sabendo que seu
traço horizontal coincide com a reta AB. (A) [4, 0, 0]; (B) [14, 9, 0]

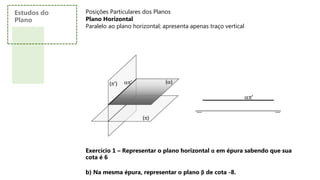
8. Posições Particulares dos Planos
Plano de Perfil
Perpendicular aos dois planos de projeção; apresenta dois traços que coincidem
Estudos do
Plano
Exercício 5 – Representar o plano de perfil β em épura definido pela reta
de perfil a reta AB. (A) [6, 14, 1]; (B) [6, 2, 16]
b) Representar, na mesma épura, o plano de perfil definido pela reta CD.
(C) [9, 10,-2]; (D) [9, 3,-11]

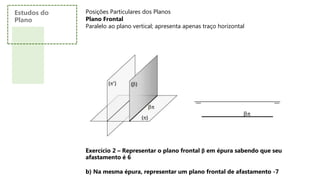
9. Posições Particulares dos Planos
Plano de Rampa
Obliquo aos dois planos de projeção; apresenta dois traços paralelos à linha de terra
Estudos do
Plano
Exercício 6 – Representar o plano de rampa β em épura sabendo que seus
traços estão em cota 6 e afastamento 12
Exercício 7 – Representar o plano de rampa β em épura sabendo que os
traços da reta de perfil AB coincidem com seus traços
(A)[1, 11, 3]
(B)[1, 2, 14]

10. Posições Particulares dos Planos
Plano que passa pela linha de terra
Caso particular do plano de rampa; Obliquo aos dois planos e que contém a linha de
terra; Os dois traços coincidem com a linha de terra
Estudos do
Plano

11. Posições Particulares dos Planos
Plano Qualquer
Obliquo aos dois planos de projeção e à linha de terra.
Estudos do
Plano
Exercício 8 – Representar o plano qualquer β em épura sabendo seus
traços contém as projeções da reta qualquer AB
(A)[4, 16, 15]
(B)[15, 2, 3]

12. Estudos do
Plano
Exercício Prático (duplas)
• No papelão, cortar um quadrado de 10cm x 10cm.
• Encontrar na sala de aula, ou no espaço da faculdade, encontro entre dois
planos que caracterizem os planos de projeção π e π’ (exemplos =
encontro de paredes com o chão; encontro de carteiras com a parede, etc.)
• Com o papelão cortado e os planos de projeção selecionados, tirar 8 fotos
representando cada posição particular dos planos.
• Em seguida, fazer épura hipotética de cada uma das posições fotografadas
• Na Guia do Exercício, preencher as características de cada posição
particular e onde podemos encontrar estes planos no mundo real.

13. Bibliografia:
CRUZ, Dennis; AMARAL, Luís. Apostila Geometria Descritiva. UFBA: Barreiras, 2012.
(exercícios e imagens)
Bibliografia Básica:
BORGES, Gladys C.de M. et al. Noções de Geometria Descritiva: teoria e exercícios.
7.ed.Porto Alegre:Sagra Luzzatto, 2002;
MONTENEGRO, Gildo. Geometria Descritiva. Vol.1. São Paulo: Edgard Blucher, 1991;
PRÍNCIPE JR, Alfredo dos Reis. Noções de Geometria Descritiva. Vol.1e2. São Paulo:
Nobel, 1988.
Bibliografia Complementar:
MACHADO, Ardevan. Geometria descritiva. São Paulo: Atual Ed., 1991;
CARVALHO, Benjamin A. de. Desenho Geométrico. Rio de Janeiro: Ao Livro Técnico;
MARCHESI JR., Isaías. Curso de desenho geométrico. Vol.1e2. São Paulo: Ática, 1998.